E2.7 Démontrer que le volume d’un prisme ou d’un cylindre peut être calculé en multipliant l’aire de la base par sa hauteur, et se servir de cette relation pour calculer l’aire de la base, le volume et la hauteur de prismes et de cylindres lorsque deux des trois mesures sont connues.
HABILETÉ : DÉMONTRER QUE LE VOLUME D’UN PRISME OU D’UN CYLINDRE PEUT ÊTRE CALCULÉ EN MULTIPLIANT L’AIRE DE LA BASE PAR SA HAUTEUR
Relation entre les attributs aire et volume
En 7e année, le personnel enseignant doit amener les élèves à découvrir la relation entre le volume d’un prisme droit, sa hauteur et l’aire de sa base. Afin que les élèves puissent établir et comprendre cette relation, elles et ils ont besoin d’explorer diverses situations d’apprentissage avec du matériel concret.
Exemple
Le personnel enseignant présente aux élèves de petites boîtes en forme de prisme droit comme celles sur la photo ci-dessous et leur demande de déterminer la façon dont elles et ils pourraient en déterminer le volume.
Une ou un élève propose de construire une structure qui occupe le même espace qu’une des boîtes en utilisant des cubes emboîtables de 1 cm3. Elle ou il dénombre ensuite les cubes utilisés. Comme il y en a 180, l’élève conclut que le volume de la boîte est égal à 180 cm3. Le personnel enseignant incite ensuite les élèves à utiliser une stratégie autre que le dénombrement pour déterminer le volume de la structure en posant des questions telles que :
- Cette structure ressemble à un édifice à étages. Combien d’étages compte cette structure? (Elle compte cinq étages.)
- Quelle est l’aire de chaque étage? Comment le sait-on? (L’aire de chaque étage est de 36 cm2 puisqu’il mesure 6 cm de long sur 6 cm de large. C’est comme une disposition rectangulaire composée de 6 rangées de 1 cm et de 6 colonnes de 1 cm.)
- Si la structure n’avait qu’un étage, quel serait son volume? Pourquoi? (Son volume serait de 36 cm3 puisqu’il serait composé de 36 cubes et que chaque cube a un volume de 1 cm3.)
- Comment peut-on alors déterminer le volume de la structure à cinq étages? (On a une disposition rectangulaire composée de cinq étages, chacune ayant un volume de 36 cm3. Le volume de la structure mesure donc 180 cm3.)
- Quelle relation ces observations vous suggèrent-elles? (Le volume d’un prisme droit est égal au produit de l’aire de sa base et de sa hauteur.)
- Comment pourrait-on écrire cette relation symboliquement? (V = aire de la base × h)
Cette relation est très importante puisqu’elle permet aux élèves de déterminer le volume d’autres prismes droits (par exemple, prisme droit à base triangulaire). Elles et ils pourront aussi l’utiliser pour déterminer le volume de cylindres.
Soulignons que le personnel enseignant peut aussi proposer aux élèves des activités qui leur permettent d’explorer des situations dans lesquelles il n’y a pas de relation entre certains attributs. Par exemple, il peut leur demander s’il y a une relation entre le volume d’un objet et sa masse. Pour illustrer cette situation, il pourrait leur montrer divers objets sphériques (par exemple, balle de tennis de table, balle de baseball, ballon de basket-ball, ballon de plage) et leur demander de les placer, d’abord en ordre croissant de volume, puis en ordre croissant de masse. Les élèves pourront conclure qu’il n’y a pas de relation entre le volume d’un objet et sa masse.
Source : Guide d’enseignement efficace des mathématiques de la 4e à la 6e année, p. 79-81.
Le volume est mesuré en unités cubes, et la mesure représente le nombre de cubes nécessaires pour occuper le même espace que l’objet ou le remplir complètement. Semblable à l’unité d’aire, l’unité cube représente un volume et peut prendre n’importe quelle forme. Les unités de volume peuvent être décomposées, réorganisées, divisées et redistribuées pour mieux représenter ou remplir un volume, et réduire les chevauchements et ne laisser aucun espace.
Mesurer le volume de ces figures indirectement plutôt que directement (par exemple, en plaçant et en empilant des cubes) est plus rapide, moins laborieux et donne des résultats plus précis.
Tous les prismes droits et les cylindres droits ont deux bases congruentes parallèles, de sorte que si un prisme ou un cylindre est coupé en « tranches » n’importe où le long de sa hauteur – à condition que cette coupe soit faite de façon parallèle à la base – la section transversale ainsi créée aura des faces congruentes. De haut en bas, l’aire de toute tranche (ou couche) est constante et équivaut toujours à l’aire de la base. Cette propriété géométrique des prismes et des cylindres constitue la base des formules de calcul du volume.
De la même manière que la structure en rangées et en colonnes d’une disposition rectangulaire aide à structurer le compte d’unités carrées pour mesurer l’aire, cette méthode aide aussi à structurer le compte d’unités cubes en vue de mesurer indirectement le volume.
- Une unité est répétée pour reproduire la longueur donnée (une rangée).
- Une rangée est répétée pour reproduire la profondeur donnée, ce qui crée l’aire de la base (une couche).
- Une couche est répétée pour reproduire la hauteur donnée (le volume).
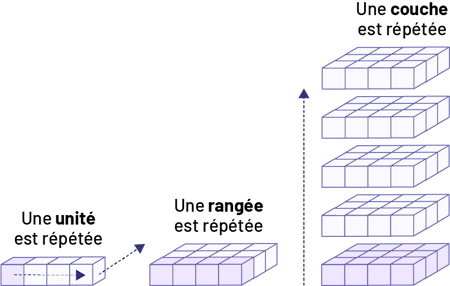
L’aire de la base détermine le nombre de cubes pouvant être placés sur la base, qui forme une seule unité (c’est-à-dire une couche de cubes). La hauteur du prisme détermine le nombre de couches de cubes nécessaires pour remplir le volume. La formule servant à trouver le volume d’un prisme rectangulaire est donc : (aire de la base) × (hauteur).
Il en va de même pour tout prisme ou cylindre : l’aire de la base détermine le nombre de cubes pouvant être placés sur la base, et la hauteur détermine le nombre de couches de cubes nécessaires pour remplir le volume. La formule servant à trouver le volume de tout cylindre ou de tout prisme est donc : (aire de la base) × (hauteur).
Source : Curriculum de l’Ontario, Programme-cadre de mathématiques de la 1re à la 8e année, 2020, Ministère de l’Éducation de l’Ontario.
La relation entre la base et la hauteur de figures ou de solides est sous-jacente à toutes les formules pour déterminer l’aire ou le volume de figures et de solides composés d’une itération d’étages. Il s’agit d’une façon organisée de comptabiliser le nombre d’unités carrées ou d’unités cubiques.
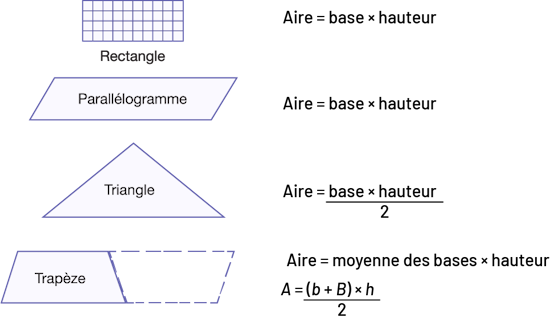image Un
rectangle. Aire égal base multipliée par hauteur. Un parallélogramme. Aire égal base multiplié par hauteur. Triangle.
Aire égal base multilpié par hauteur, divisé par 2. Trapèze. Aire égal moyenne des bases multipliées par hauteur. « A
» égal (parenthèse ouvrante) « b » plus « B » (parenthèse fermante) multiplié par « h », divisé par 2
image Un
prisme droit à base rectangulaire, une couche est en évidence. Un prisme droit à base triangulaire, une couche est
mise en évidence. Un cylindre, une couche est mise en évidence.
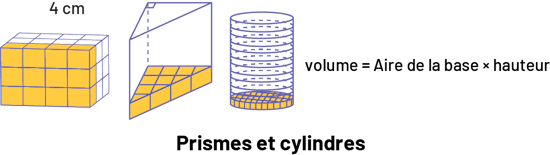image Un
cercle. « R » est le rayon. Pi est égal à 3 virgule 1416. Circonférence d’un cercle égal Pi multiplié par diamètre. «
C » égal Pi « d ». Aire d’un disque égal Pi multiplié par rayon au carré. « A » indice disque égal Pi rayon au
carré.
Source : Guide d’enseignement efficace des mathématiques de la 7e à la 10e année, p. 52-53.
HABILETÉ : CALCULER L’AIRE DE LA BASE, LE VOLUME ET LA HAUTEUR DE PRISMES ET DE CYLINDRES LORSQUE DEUX DES TROIS MESURES SONT CONNUES
Appliquer une formule
Une formule en mesure est une équation qui représente une relation fondamentale entre la mesure de différents attributs d’un objet. Une fois établie, elle permet de déterminer la mesure d’un attribut quelconque d’un objet à partir d’un calcul fondé sur la mesure d’autres attributs (par exemple, déterminer la mesure du volume d’un prisme droit à partir de la mesure de sa hauteur et de l’aire de sa base).
Il importe que le personnel enseignant mette l’accent sur l’exploration des relations entre divers attributs mesurables d’un objet et sur l’élaboration des formules qui en découlent avant d’étudier avec les élèves la façon d’appliquer une formule. Selon Van de Walle et Lovin (2008b, p. 284), « une approche conceptuelle de l’élaboration de formules aide les élèves à comprendre que ces outils sont autant de moyens utiles et efficaces servant à mesurer divers attributs des objets qui nous entourent. Une fois qu’ils auront construit des formules de manière significative, […] ils sauront déduire les formules de ce qu’ils savent déjà. »
Lorsque les élèves ont compris le sens des formules, elles et ils doivent apprendre à les utiliser correctement. Le personnel enseignant doit leur présenter différentes situations qui les incitent à utiliser une formule pour déterminer la mesure d’un attribut quelconque. Il doit profiter de l’occasion pour établir des liens avec le domaine Algèbre.
Source : Guide d’enseignement efficace des mathématiques de la 4e à la 6e année, p. 99-100.