E2. Sens de la mesure
Comparer, estimer et déterminer des mesures dans divers contextes.
SITUATION D’APPRENTISSAGE 1 : COMBIEN D’ESPACE OCCUPE CE PRISME?
Durée totale : 90 minutes
Sommaire
Dans cette situation d’apprentissage, les élèves construisent des prismes à base rectangulaire à partir de développements. Les élèves estiment et déterminent ensuite le volume de ces prismes à l’aide de cubes unitaires, et elles et ils expliquent la stratégie utilisée dans chaque cas.
|
Attente |
Contenu |
|
E2. Comparer, estimer et déterminer des mesures dans divers contextes. |
E1.1 Décrire la différence et la similarité entre le volume et la capacité, et résoudre des problèmes en se servant de la relation entre les millilitres (ml) et les centimètres cubes (cm³) |
Intention pédagogique
Cette situation d’apprentissage a pour but d’amener les élèves :
- à reconnaître certains attributs mesurables d’un objet;
- à comprendre ce que signifie l’attribut volume;
- à estimer et à déterminer le volume d’un prisme à base rectangulaire à l’aide de cubes unitaires;
- à explorer les concepts d’itération, de conservation, de transitivité, d’additivité et de structure associée aux unités de mesure.
|
Contexte |
Préalable |
|
En 7e année, les élèves explorent le concept de volume d’un solide à l’aide de cubes unitaires. Afin d’éviter qu’elles et ils ne confondent les concepts de capacité et de volume, il est préférable de s’en tenir au volume de solides fermés. |
La présente situation d’apprentissage permet aux élèves de comprendre que le volume d’un objet correspond à la grandeur de l’espace qu’il occupe, que cette grandeur s’exprime en unités cubiques et qu’une façon de déterminer ce volume est de reproduire l’objet à l’aide de cubes unitaires. Pour être en mesure de réaliser cette situation d’apprentissage, les élèves doivent pouvoir :
|
Vocabulaire mathématique
attribut mesurable, aire, face, périmètre, longueur, largeur, volume, masse, capacité, cubes unitaires, disposition rectangulaire
Matériel
- boîtes fermées en forme de prisme à base rectangulaire (deux)
- annexe 4.1 (une copie par équipe de quatre)
- ciseaux (une paire par élève)
- ruban adhésif (un rouleau par équipe de quatre)
- sacs d’environ 150 cubes unitaires (un sac par équipe de quatre)
Avant l’apprentissage (mise en train)
Durée : 15 minutes
Présenter aux élèves deux boîtes fermées en forme de prisme à base rectangulaire. Leur demander de déterminer le plus d’attributs mesurables possible de ces prismes et de les noter dans leur journal de mathématiques.

Demander ensuite à quelques élèves de nommer un des attributs qu’elles et ils ont déterminés (par exemple, longueur, hauteur, largeur, épaisseur, aire d’une face, périmètre d’une face, masse) et d’expliquer ce que cet attribut représente en l’illustrant à l’aide d’un des prismes.
Exemples

Voici la longueur de cette face du prisme.

La longueur de la ficelle représente le périmètre de la face avant ou arrière du prisme.
Demander aux élèves d’indiquer le prisme qui occupe, selon elles et eux, le plus d’espace et de justifier leur réponse. Quelques élèves pourraient dire, par exemple, que c’est tel prisme qui occupe le plus d’espace parce qu’il est plus long, alors que d’autres pourraient dire que c’est plutôt l’autre prisme qui occupe le plus d’espace parce qu’il est plus épais. Leur demander ensuite : « Comment pourrions-nous déterminer la grandeur de l’espace qu’occupe chacun de ces prismes? ».
|
Réponses possibles |
Interventions possibles |
|
On peut mesurer sa hauteur. 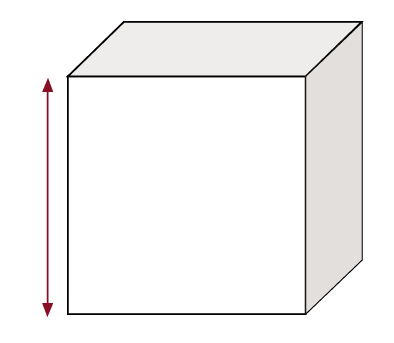
|
Demander aux autres élèves ce qu'elles et ils en pensent. Les amener à reconnaître qu'un autre prisme pourrait avoir la même hauteur, mais occuper un espace plus grand ou plus petit. |
|
On peut trouver l'aire de chacune des faces et les additionner. 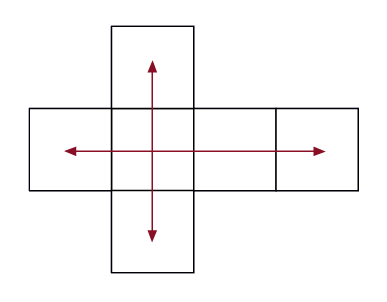
|
Demander aux autres élèves ce qu'elles et ils en pensent. Les amener à reconnaître que la somme des aires des faces représente l'aire du développement du prisme, c'est-à-dire la grandeur de l'espace à deux dimensions que les faces du prisme occupent. |
|
On peut le reproduire avec des cubes. 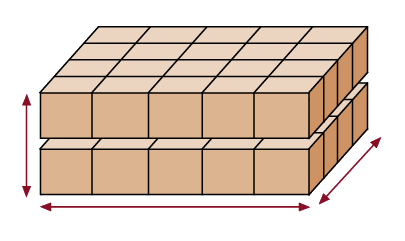
|
Demander aux autres élèves ce qu'elles et ils en pensent. Les amener à reconnaître que cela permet de déterminer la grandeur de l'espace à trois dimensions que le prisme occupe et que cette grandeur correspond au nombre de cubes requis pour le reproduire. |
Pendant l’apprentissage (exploration)
Durée : 45 minutes
Indiquer aux élèves que la grandeur de l’espace à trois dimensions qu’un objet occupe s’appelle le volume.
Former des équipes de quatre et proposer aux élèves d’explorer plus à fond le concept de volume. Remettre à chaque équipe une copie de l’annexe 4.1 (Développements de prismes). Leur demander de découper chacun des développements, de construire les prismes correspondants et de les placer en ordre croissant selon leur estimation de la grandeur de l’espace que chacun occupe.
Demander ensuite à quelques équipes de présenter leur réponse et d’expliquer la stratégie utilisée pour comparer les volumes.
Exemple
Une équipe présente les prismes placés comme sur la photo ci-dessous et fournit l’explication suivante : « C’est le prisme D qui occupe le plus petit espace. Les prismes A et B ont le même volume. Pour le trouver, on a placé les prismes dos à dos et on les a comparés. ».

Animer une discussion au sujet des différentes réponses proposées et faire ressortir l’importance de trouver un moyen plus efficace de comparer les volumes. Remettre un cube unitaire à chaque équipe et leur demander d’estimer le volume des prismes, c’est-à-dire d’estimer le nombre de cubes qu’il faudrait pour reproduire chaque prisme.
Note : Lors de la mise à l’essai de cette situation d’apprentissage, l’enseignante a utilisé des cubes unitaires de 1 cm3. Tous les résultats présentés dans ce qui suit reflètent donc cette unité de mesure. Le personnel enseignant pourrait utiliser un autre format de cube (par exemple, cubes unitaires de 2 cm d’arête) et modifier la mesure du volume des prismes en conséquence.
Circuler et laisser les élèves déterminer la façon dont elles et ils peuvent utiliser le cube unitaire pour déterminer le volume de chaque prisme. Les élèves peuvent, par exemple, placer mentalement le cube de façon ordonnée à divers endroits le long d’un prisme et estimer le nombre de fois qu’elles et ils doivent le placer pour remplir tout l’espace occupé par ce prisme.
Lorsque toutes les équipes ont terminé, demander de nouveau à quelques-unes de présenter leur résultat et de décrire la stratégie utilisée. Les inciter à placer les prismes en ordre croissant de volume et à comparer ce résultat avec le résultat précédent.
Exemple
Une équipe présente son résultat à l’aide d’un tableau et fournit l’explication suivante : « Nous avons estimé le nombre de cubes qu’il faudrait pour occuper le même espace que le prisme. Nous avons ensuite placé les prismes en ordre croissant de volume et avons constaté que ce classement était différent de celui proposé lors de notre première estimation. ».
|
Prisme |
Nombre de cubes |
|
D |
18 |
|
A |
20 |
|
B |
24 |
|
C |
32 |
Après les présentations, remettre à chaque équipe un sac contenant environ 150 cubes unitaires et leur demander de déterminer le volume exact de chaque prisme en les reproduisant à l’aide de ces cubes. Circuler et intervenir au besoin.
|
Observations possibles |
Interventions possibles |
|
Une équipe décide de recouvrir le prisme A avec des cubes. 
|
Amener les élèves à réaliser que le prisme qu'elles et ils sont en train de construire est plus large que le prisme A. Souligner que le volume du prisme À correspond en réalité au volume intérieur du prisme qu'elles et ils construisent. |
|
Une équipe construit une disposition rectangulaire plus grande que la base du prisme B. 
|
Demander à l'équipe de construire un prisme en superposant des dispositions rectangulaires de cette grandeur, puis de le comparer au prisme B. Les amener à réaliser que le prisme construit à l'aide de cubes est plus large et plus long que le prisme B. Faire ressortir le fait que la face supérieure de la disposition rectangulaire doit avoir la même aire que la base du prisme B. |
|
L'équipe ouvre le prisme D et essaie de le remplir. 
|
Amener les élèves à réaliser que ce qu'elles et ils sont en train de mesurer n'est pas le volume du prisme D, mais sa capacité ou son volume intérieur. Pour les aider à comprendre la différence, les inviter à imaginer que le prisme est fait de polystyrène d'une épaisseur de 1 cm. |
Après l’apprentissage – (objectivation/échange mathématique)
Durée : 30 minutes
Regrouper les élèves et poser les questions suivantes :
- Que remarquez-vous au sujet du volume des prismes? (Tous les prismes ont un volume de 24 cubes.)
- Comment ce résultat se compare-t-il avec les deux estimations précédentes? (Ce n’est pas pareil, car on pensait que les volumes étaient tous différents, que le prisme C avait un plus grand volume que le prisme B…)
Inviter ensuite quelques équipes à décrire la stratégie utilisée pour déterminer le volume des prismes.
Exemple 1
Les membres d’une équipe indiquent qu’elles et ils ont reproduit chaque prisme à l’aide de cubes et dénombré les cubes utilisés dans chaque cas.

Exemple 2
Les membres d’une deuxième équipe disent qu’elles et ils ont utilisé une stratégie différente et l’expliquent comme suit : « On a recouvert le haut du prisme C avec des cubes et obtenu une disposition rectangulaire composée de 12 cubes. On a ensuite superposé une deuxième disposition rectangulaire et obtenu un volume égal au volume du prisme C. On a alors conclu que le volume du prisme C est égal à 24 cubes, soit deux dispositions rectangulaires contenant 12 cubes chacune. ».


Exemple 3
Une troisième équipe explique la stratégie utilisée comme suit : « On a fait quelque chose de très semblable à la deuxième équipe pour obtenir le volume du prisme B. On a d’abord construit une disposition rectangulaire verticale de la grandeur d’un des bouts du prisme. On a ensuite ajouté des dispositions rectangulaires identiques jusqu’à ce qu’on obtienne un prisme de même volume que le prisme original. Puisqu’on avait six dispositions rectangulaires et que chacune était composée de quatre cubes, on a déterminé que le volume du prisme B est égal à 24 cubes. ».


Faire remarquer aux élèves qu’elles et ils ont utilisé différentes stratégies pour déterminer que le volume de chaque prisme est égal à 24 cubes. Leur demander maintenant d’expliquer la façon dont elles et ils pourraient montrer que les quatre prismes ont le même volume, sans dénombrer les cubes. Modeler, au besoin, la façon de décomposer un des quatre prismes pour former un des trois autres prismes.
Exemples
Le volume du prisme A est le même que celui du prisme B, car si on décompose le prisme A en deux prismes identiques et qu’on les superpose, on obtient le prisme B.

Les prismes C et D ont le même volume, car si on sépare les deux dispositions rectangulaires qui sont superposées pour former le prisme C et qu’on les place une à côté de l’autre, on obtient le prisme D.

Le volume du prisme C est égal au volume du prisme B, car si on sépare le prisme C en deux prismes identiques et qu’on les place bout à bout, on obtient le prisme B.

Profiter de l’occasion pour explorer avec les élèves les concepts de conservation du volume. On peut aussi explorer le concept de transitivité en soulignant, par exemple, que si on montre que le volume du prisme A est égal au volume du prisme B et que le volume du prisme B est égal au volume du prisme C, il est alors possible de conclure que le volume du prisme A est égal au volume du prisme C.
Différenciation pédagogique
|
Pour faciliter la tâche |
Pour enrichir la tâche |
|
Remettre aux élèves quatre prismes à base rectangulaire formés de 24 cubes emboîtables, plutôt que les développements de prismes de l’annexe 4.1, et leur demander de comparer les volumes en utilisant les cubes d’un des prismes pour reproduire chacun des trois autres. |
Demander aux élèves de déterminer les prismes à base rectangulaire, autres que les prismes A, B, C et D, qui ont un volume de 24 cubes et de les construire. (Il y a deux prismes possibles. Leurs dimensions sont : 1 sur 1 sur 24 et 1 sur 3 sur 8.) |
Suivi à la maison
Demander aux élèves de choisir trois boîtes en forme de prismes à base rectangulaire (par exemple, boîte de céréales, boîte de biscuits, boîte de chaussures) et de déterminer une façon de les placer en ordre croissant de volume.
Activité supplémentaire 1 : village de monsieur Édifico
Présenter la situation ci-dessous aux élèves.
Monsieur Édifico adore construire des villages miniatures autour de son train électrique. Il décide de construire un village composé de 12 édifices de forme différente, mais de même volume.
Pouvez-vous lui proposer 12 modèles différents d’édifices qu’il pourrait construire? En raison de la taille du village miniature, vos édifices doivent tous avoir un même volume de 7, de 8, de 9 ou de 10 cubes.
Note : Les deux édifices illustrés ci-dessous ont un volume de 5 cubes. Ils ne sont cependant pas différents puisqu’ils ont la même forme. C’est seulement l’orientation des différentes parties qui est modifiée et non la forme.

Former des équipes de trois et remettre à chaque équipe un sac d’environ 150 cubes emboîtables. Allouer suffisamment de temps pour leur permettre de construire diverses structures.
Circuler et intervenir au besoin. Par exemple, si une équipe construit une structure dans laquelle deux cubes ont une arête commune plutôt qu’une face commune, souligner qu’il s’agit là de deux édifices et non d’un seul.

Lorsque toutes les équipes ont terminé, demander à quelques-unes de présenter leur village. Inviter les autres élèves à poser des questions et à faire part de leurs observations.
Animer l’échange en posant des questions telles que :
- Tous les édifices ont-ils une forme différente? Comment le savez-vous?
- Tous les édifices ont-ils le même volume? Justifiez votre réponse.
Prolongement
Demander aux élèves de comparer les édifices en fonction :
- du nombre de sommets, d’arêtes ou de faces;
- du périmètre ou de l’aire de leur base.
Note : Cette activité peut se faire à l’aide d’un jeu vidéo en lien avec la construction de structures (par exemple, Minecraft)
Source : Guide d’enseignement efficace des mathématiques de la 4e à la 6e année, p. 127-38.
SITUATION D’APPRENTISSAGE 2 : HEUREUX COMME UN POISSON DANS L’EAU
Durée approximative : 130 minutes
Sommaire
Dans cette situation d’apprentissage, les élèves explorent la relation entre le millilitre (ml) et le centimètre cube (cm3) en déterminant, par déplacement d’eau, le volume de solides réguliers et irréguliers.
|
Attente |
Contenu |
|
E2. Comparer, estimer et déterminer des mesures dans divers contextes. |
E1.1 Décrire la différence et la similarité entre le volume et la capacité, et résoudre des problèmes en se servant de la relation entre les millilitres (ml) et les centimètres cubes (cm³) |
Intention pédagogique
Cette situation d’apprentissage a pour but d’amener les élèves :
- à développer leurs habiletés à mesurer;
- à reconnaître que le volume d’un objet correspond à la grandeur de l’espace à trois dimensions qu’il occupe;
- à établir le lien entre le volume d’un objet et le volume d’eau qu’il déplace lorsqu’il est immergé;
- à découvrir la relation d’équivalence entre le millilitre (ml) et le centimètre cube (cm3);
- à consolider leur compréhension du concept de conservation du volume.
|
Contexte |
Préalables |
|
Au cours des années précédentes, les élèves ont appris à déterminer, à l’aide d’unités de mesure conventionnelles, la capacité de contenants (par exemple, en millilitres [ml] ou en litres [l]) et le volume de solides (par exemple, en centimètres cubes [cm3]). |
En 7e année, elles et ils doivent saisir la différence entre une mesure de capacité et une mesure de volume. Par exemple, une bouteille peut avoir une capacité de 350 ml de jus, mais ne contenir qu’un volume de 300 ml de jus, une boîte fermée en bois peut avoir un volume extérieur de 1 m3, mais un volume intérieur, c’est-à-dire une capacité, de 0,9 m3. Les élèves doivent aussi explorer la relation d’équivalence entre le volume d’un objet, en centimètres cubes, et le volume de liquide, en millilitres, que cet objet déplace lorsqu’il est immergé. Par exemple, lorsqu’un objet dont le volume est égal à 1 cm3 est immergé dans l’eau, il déplace un volume d’eau équivalent à 1 ml. La présente situation d’apprentissage permet aux élèves de développer une meilleure compréhension de l’attribut volume et de découvrir la relation d’équivalence entre le centimètre cube et le millilitre. Pour être en mesure de réaliser cette situation d’apprentissage, les élèves doivent :
|
Vocabulaire mathématique
attribut mesurable, volume, centimètre cube (cm³), millilitre (ml), prisme à base rectangulaire, solide régulier, solide irrégulier
Matériel
- différents prismes faits avec de la pâte à modeler dont le volume est supérieur ou égal à 30 cm³ (un par équipe)
- annexe 6.1 (une feuille de travail par équipe)
- annexe 6.2 (une feuille de travail par équipe)
- cubes de 1 cm3
- feuilles de papier quadrillé en cm2
- ficelle
- règles
- récipients gradués de 250 ml ou plus (un par équipe)
- éprouvettes graduées de 50 ml ou moins (une par équipe)
- entonnoirs (un par équipe)
- contenants d’eau
- plateaux (un par équipe)
- grandes feuilles de papier (deux par équipe)
Note : Cette situation d’apprentissage comprend deux sections Exploration, chacune étant suivie d’un échange mathématique. Cette organisation a pour but de faciliter la gestion du temps et de permettre aux élèves de faire progressivement le point sur les concepts visés.
Avant l’apprentissage (mise en train)
Durée : 20 minutes
Présenter aux élèves un bloc de pâte à modeler et leur demander de dresser une liste des attributs mesurables de ce prisme (par exemple, longueur, largeur, hauteur, volume, périmètre, masse).

Animer une discussion en posant des questions telles que :
- Comment pouvez-vous mesurer chacun de ces attributs? (On peut, par exemple, mesurer la longueur, la largeur et le périmètre à l’aide d’une règle, la masse à l’aide d’une balance, le volume à l’aide de cubes.)
- Qu’est-ce que le volume d’un solide? (C’est la grandeur de l’espace à trois dimensions qu’il occupe.)
- Pourquoi voudrait-on connaître le volume d’un solide? (On voudrait connaître son volume afin, par exemple, de le ranger dans une boîte, de le placer sur une tablette…)
- Quelles unités de mesure conventionnelles sont habituellement utilisées pour déterminer le volume d’un solide? (On utilise des unités cubiques telles que le centimètre cube ou le mètre cube.)
- Quelles unités de mesure conventionnelles sont habituellement utilisées pour déterminer le volume d’une quantité donnée de liquide? (On utilise des unités telles que le millilitre ou le litre.)
Fabriquer à l’avance, à l’aide de pâte à modeler, différents prismes à base rectangulaire. S’assurer que le volume de chaque prisme mesure au moins 30 cm3. Former des équipes. Distribuer un prisme à chaque équipe ainsi qu’une feuille de travail (voir l’annexe 6.1).
Leur demander d’estimer le volume de leur prisme à l’aide d’un repère et de noter cette estimation dans la première colonne de la feuille de travail.

Construire un tableau collectif (voir l’annexe 6.2) sur une grande feuille, un tableau interactif, un transparent ou au tableau, et y inscrire les estimations de chacune des équipes.
Exemple
|
Équipe |
Estimation du volume du prisme |
Mesure du volume du prisme |
Estimation du volume d'eau déplacée par le prisme |
Mesure du volume d'eau déplacée par le prisme |
Estimation du volume d'eau déplacée par le poisson |
Mesure du volume d'eau déplacée par le poisson |
|
M et J |
30 cm3 |
|||||
|
C et Y |
45 cm3 |
|||||
|
E et D |
82 cm3 |
|||||
|
P et S |
56 cm3 |
Demander ensuite aux élèves de déterminer la mesure du volume de leur prisme à l’aide de la stratégie de leur choix (par exemple, reproduire le solide à l’aide de cubes de 1 cm3, appliquer une formule) et de noter ce résultat dans la deuxième colonne de leur feuille de travail. Mettre à leur disposition le matériel nécessaire (par exemple, cubes de 1 cm3, feuilles de papier quadrillé en cm2, ficelle, règles). Les inviter ensuite à comparer la mesure du volume de leur prisme avec leur estimation.

Animer un bref échange portant sur les différentes stratégies utilisées pour établir le volume des prismes, puis inscrire le volume du prisme de chaque équipe dans le tableau collectif.
Exemple
|
Équipe |
Estimation du volume du prisme |
Mesure du volume du prisme |
Estimation du volume d'eau déplacée par le prisme |
Mesure du volume d'eau déplacée par le prisme |
Estimation du volume d'eau déplacée par le poisson |
Mesure du volume d'eau déplacée par le poisson |
|
M et J |
30 cm3 |
36 cm3 |
||||
|
C et Y |
45 cm3 |
48 cm3 |
||||
|
E et D |
82 cm3 |
72 cm3 |
||||
|
P et S |
56 cm3 |
60 cm3 |
Par la suite, inciter les élèves à réfléchir à l’idée d’utiliser le déplacement de l’eau comme stratégie pour mesurer le volume d’un solide en posant des questions telles que :
- Si vous plongez votre prisme dans un récipient d’eau, quel en sera l’effet sur le niveau de l’eau dans le récipient? (Le niveau de l’eau va monter.)
- Pourquoi l’eau sera-t-elle ainsi déplacée? (L’eau est déplacée parce que le prisme occupe de l’espace dans le récipient.)
Demander alors aux élèves d’estimer le volume d’eau que leur prisme va déplacer après son immersion dans l’eau et d’inscrire cette estimation dans la troisième colonne de leur feuille de travail. Leur proposer ensuite d’effectuer une expérience pour vérifier leur estimation.
Pendant l’apprentissage (exploration) – 1
Durée : 40 minutes
Distribuer à chaque équipe un récipient gradué (par exemple, éprouvette, bécher) de 250 ml ou plus dans lequel il est possible d’immerger le prisme reçu, une éprouvette graduée de 50 ml ou moins, un entonnoir, un contenant d’eau et un plateau. Leur demander de placer tout le matériel dans le plateau.

Inviter ensuite les élèves à utiliser ce matériel pour déterminer le volume d’eau déplacée lorsqu’elles et ils immergent leur prisme, à noter ce résultat dans la quatrième colonne de leur feuille de travail et à décrire, sur une grande feuille, la stratégie utilisée.
Allouer suffisamment de temps pour permettre à toutes les équipes d’effectuer l’expérience. Circuler, observer les stratégies utilisées et intervenir au besoin. Le tableau ci-dessous présente deux exemples de telles interventions.
|
Observations possibles |
Interventions possibles |
|
Les élèves remplissent l’éprouvette graduée à ras bord, y plongent le prisme, puis le retirent. Elles et ils font ensuite la lecture du volume d’eau qui reste dans l’éprouvette et notent cette mesure comme étant le volume d’eau déplacée par le prisme. |
Amener les élèves à réfléchir à la mesure notée en posant des questions telles que :
|
|
Les élèves remplissent l’éprouvette graduée à ras bord, y plongent le prisme, puis le retirent. Elles et ils semblent ensuite incapables de déterminer le volume d’eau déplacée. |
Inciter les élèves à trouver la source de leurs difficultés en posant des questions telles que :
|
Après l’apprentissage (objectivation/échange mathématique) – 1
Durée : 30 minutes
Note : Cette objectivation se fait en deux temps. On fait d’abord une mise en commun des stratégies utilisées pour déterminer le volume d’eau déplacée en faisant ressortir la diversité des stratégies possibles et l’importance de mesurer avec exactitude afin de tenir compte du ménisque. On fait ensuite une mise en commun des volumes obtenus en incitant les élèves à chercher une relation entre le millilitre et le centimètre cube.
Inviter quelques équipes à expliquer la stratégie utilisée pour déterminer le volume d’eau déplacée par le prisme. Choisir des équipes qui ont utilisé des stratégies différentes. Après chaque présentation, inviter les autres élèves à intervenir, à poser des questions au besoin et à discuter des avantages et des inconvénients liés à la stratégie utilisée (par exemple, difficile de récupérer toute l’eau qui a débordé de l’éprouvette).
Voici quelques-unes des stratégies que les élèves pourraient utiliser.
- Les élèves remplissent l’éprouvette graduée à ras bord, y plongent le prisme, puis le retirent. Afin de déterminer le volume d’eau déplacée par le prisme, elles et ils mettent des cubes de 1 cm3 pour remplir de nouveau l’éprouvette à ras bord. Elles et ils inscrivent comme mesure du volume d’eau déplacée le nombre de cubes mis dans l’éprouvette.
- Les élèves remplissent l’éprouvette graduée à ras bord et y plongent le prisme, faisant ainsi déborder l’eau. Elles et ils vident ensuite dans l’autre éprouvette graduée toute l’eau qui a débordé et font la lecture du niveau de l’eau (par exemple, 45 ml) pour obtenir le volume d’eau déplacée par le prisme.
- Les élèves remplissent l’éprouvette graduée jusqu’à un certain niveau et notent le volume d’eau (par exemple, 100 ml). Elles et ils y plongent ensuite le prisme et notent le niveau de l’eau (par exemple, 140 ml). Afin de déterminer le volume d’eau déplacée par le prisme, les élèves calculent la différence entre les niveaux de l’eau après et avant l’immersion du prisme (140 ml – 100 ml = 40 ml).

- Les élèves placent le prisme dans l’éprouvette, le recouvrent ensuite d’eau et font la lecture du niveau de l’eau (par exemple, 175 ml). Puis, elles et ils retirent le prisme et font à nouveau la lecture du niveau de l’eau (par exemple, 125 ml). Pour déterminer le volume d’eau déplacée, les élèves calculent la différence entre ces deux niveaux (175 ml – 125 ml = 50 ml).
Une fois les présentations des stratégies terminées, inviter une ou un membre de chaque équipe à inscrire dans le tableau collectif la mesure obtenue pour le volume d’eau déplacée par leur prisme.
Exemple
|
Équipe |
Estimation du volume du prisme |
Mesure du volume du prisme |
Estimation du volume d'eau déplacée par le prisme |
Mesure du volume d'eau déplacée par le prisme |
Estimation du volume d'eau déplacée par le poisson |
Mesure du volume d'eau déplacée par le poisson |
|
M et J |
30 cm3 |
36 cm3 |
40 ml |
37 ml |
||
|
C et Y |
45 cm3 |
48 cm3 |
62 ml |
50 ml |
||
|
E et D |
82 cm3 |
72 cm3 |
50 ml |
71 ml |
||
|
P et S |
56 cm3 |
60 cm3 |
62 ml |
60 ml |
Inciter ensuite les élèves à établir un lien entre le volume du prisme (troisième colonne du tableau collectif) et le volume d’eau déplacée (cinquième colonne du tableau collectif) en posant des questions telles que :
- Si vous comparez la mesure du volume de votre prisme avec la mesure du volume d’eau déplacée par le prisme, qu’est-ce que vous observez? (Le nombre d’unités du volume du prisme et le nombre d’unités du volume d’eau déplacée sont presque les mêmes.)
- Quelle conjecture pourriez-vous formuler à partir des résultats de cette expérience? (Le volume d’eau déplacée par un objet immergé dans l’eau est équivalent au volume de l’objet.)
- Dans plusieurs cas, la mesure du volume du prisme n’est pas exactement égale à la mesure du volume d’eau déplacée. Comment pourrait-on expliquer ces différences? (Elles peuvent être le résultat d’une erreur de calcul ou de difficultés liées à la façon d’effectuer l’expérience et de mesurer.)
- Est-ce que le volume d’eau déplacée par votre prisme serait le même si vous utilisiez un récipient différent? Pourquoi? (Il serait le même puisque le volume d’eau déplacée dépend du volume du prisme et non de la capacité du contenant dans lequel il est immergé.)
- Quelle unité de mesure est utilisée pour déterminer le volume du prisme? (Le centimètre cube.)
- Quelle unité de mesure est utilisée pour déterminer le volume d’eau déplacée? (Le millilitre.)
- Quelle relation semble-t-il y avoir entre ces deux unités de mesure? (Un solide de 1 cm3 déplace 1 ml d’eau.)
Une fois que les élèves ont établi la relation entre le centimètre cube et le millilitre, les amener à utiliser cette relation pour déterminer le volume d’un solide irrégulier.
Pendant l’apprentissage (exploration) – 2
Durée : 20 minutes
Inviter les élèves à former les mêmes équipes que précédemment. Leur demander de façonner un « poisson » à partir de leur prisme en pâte à modeler. Préciser qu’elles et ils doivent utiliser toute la pâte à modeler et s’assurer que le poisson puisse entièrement entrer dans le récipient gradué.
Demander ensuite aux élèves de déterminer le volume, en centimètres cubes, du poisson en suivant la démarche suivante.
- Estimer le volume d’eau que le poisson va déplacer lorsqu’il sera immergé et noter cette estimation dans la cinquième colonne de la feuille de travail;
- Utiliser la stratégie de votre choix pour mesurer le volume d’eau déplacée lorsque le poisson est immergé dans l’eau et noter ce résultat dans la sixième colonne de la feuille de travail;
- Inscrire, sur une grande feuille, le volume en centimètres cubes de votre poisson et indiquer la façon dont vous arrivez à ce résultat.
Mettre d’autres solides irréguliers à la disposition des élèves qui voudraient vérifier leur conclusion. Circuler, observer les stratégies utilisées et intervenir au besoin.
Après l’apprentissage (objectivation/échange mathématique) – 2
Durée : 20 minutes
Inviter une ou un membre de chaque équipe à inscrire dans le tableau collectif leur estimation et la mesure du volume d’eau déplacée par leur poisson.
Exemple
|
Équipe |
Estimation du volume du prisme |
Mesure du volume du prisme |
Estimation du volume d'eau déplacée par le prisme |
Mesure du volume d'eau déplacée par le prisme |
Estimation du volume d'eau déplacée par le poisson |
Mesure du volume d'eau déplacée par le poisson |
|
M et J |
30 cm3 |
36 cm3 |
40 ml |
37 ml |
35 ml |
36 ml |
|
C et Y |
45 cm3 |
48 cm3 |
62 ml |
50 ml |
50 ml |
49 ml |
|
E et D |
82 cm3 |
72 cm3 |
50 ml |
71 ml |
70 ml |
70 ml |
|
P et S |
56 cm3 |
60 cm3 |
62 ml |
60 ml |
64 ml |
60 ml |
Inviter quelques équipes à présenter et à justifier leur résultat. À titre d’exemple, une équipe pourrait dire : « Notre poisson a déplacé 29 ml d’eau. Lors de la première expérience, on a vu que le volume en millilitres d’eau déplacée par un objet immergé est équivalent au volume en centimètres cubes de l’objet. On peut donc conclure que le volume de notre poisson est égal à 29 cm3. »

Profiter de la situation pour inciter les élèves à établir le lien entre les résultats des deux expériences et le concept de conservation du volume en posant des questions telles que :
- Y a-t-il un lien entre le volume de votre poisson et le volume du prisme original inscrit dans la troisième colonne du tableau collectif? Pourquoi? (Le volume du poisson est le même que le volume du prisme parce que les deux formes sont fabriquées à partir de la même quantité de pâte à modeler.)
- Si vous aviez façonné un hippocampe au lieu d’un poisson à partir de votre prisme en pâte à modeler, quel aurait été le volume d’eau déplacée? Justifiez votre réponse. (Le volume d’eau déplacée aurait été le même parce que la grandeur de l’espace occupé par la pâte à modeler demeure la même, peu importe la forme qu’on lui donne.)
- J’ai fabriqué une étoile de mer avec de la pâte à modeler. Je veux déterminer son volume, mais je n’ai pas de récipient gradué et d’eau à ma disposition. Comment pourrais-je faire pour déterminer ce volume? (Vous pourriez transformer l’étoile de mer en prisme rectangulaire, puis mesurer les dimensions du prisme et déterminer son volume. Puisque l’étoile de mer et le prisme sont fabriqués à partir de la même quantité de pâte à modeler, les deux solides ont le même volume.)
Différenciation pédagogique
|
Pour faciliter la tâche |
Pour enrichir la tâche |
|
Demander aux élèves de décrire une procédure qui permettrait de déterminer le volume d’eau déplacée par un solide placé dans un récipient non gradué (voir l’exemple ci-dessous). |
Exemple
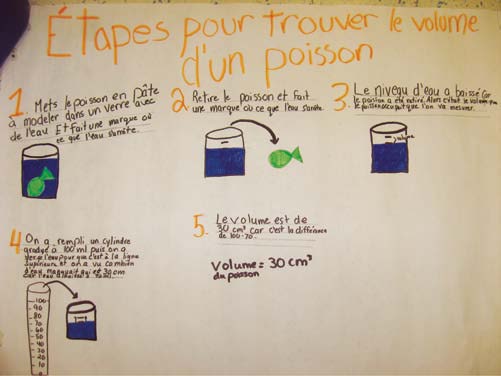
Suivi à la maison
À la maison, les élèves peuvent prendre deux objets qui semblent avoir à peu près le même volume (par exemple, une roche et une figurine) et demander à une ou à un membre de la famille d’indiquer l’objet qui semble avoir le plus grand volume. Ensuite, à l’aide d’un récipient gradué suffisamment grand pour y immerger les objets, elles et ils peuvent vérifier cette estimation en mesurant le volume d’eau déplacée par chaque objet.
Source : Guide d’enseignement efficace des mathématiques de la 4e à la 6e année, p. 157-168.
