C1.1 Reconnaître et décrire les règles dans une variété de suites, y compris des suites trouvées dans la vie quotidienne.
Habileté : reconnaître une variété de suites
Suites non numériques
Suites à motif répété
La suite à motif répété est créée lorsque les éléments qui constituent le motif se répètent selon le même ordre. Les élèves doivent apprendre à reconnaître le début et la fin du motif dans la suite; par exemple, dans la photo ci-dessous, l’élève qui a créé cette suite montre, en laissant un espace entre les motifs, que la perle orange indique le début du motif et la perle rouge, la fin.
En outre, il est important de demander aux élèves de « lire » la suite en nommant et en touchant chaque élément consécutif du motif pour qu’elles et ils se rendent compte de la répétition.
Du cycle préparatoire jusqu’à la fin du cycle primaire, les suites que les élèves apprennent à explorer et à créer doivent être de plus en plus complexes.
Voici une suggestion de démarche pour enseigner les suites à motif répété :
- Observer une suite ayant un attribut et un motif à deux éléments.
Explorer d’abord une suite n’ayant qu’un seul attribut et dont le motif ne comprend que deux éléments. L’attribut pourrait être le mouvement, la position, le son, la forme ou la couleur.
Exemple
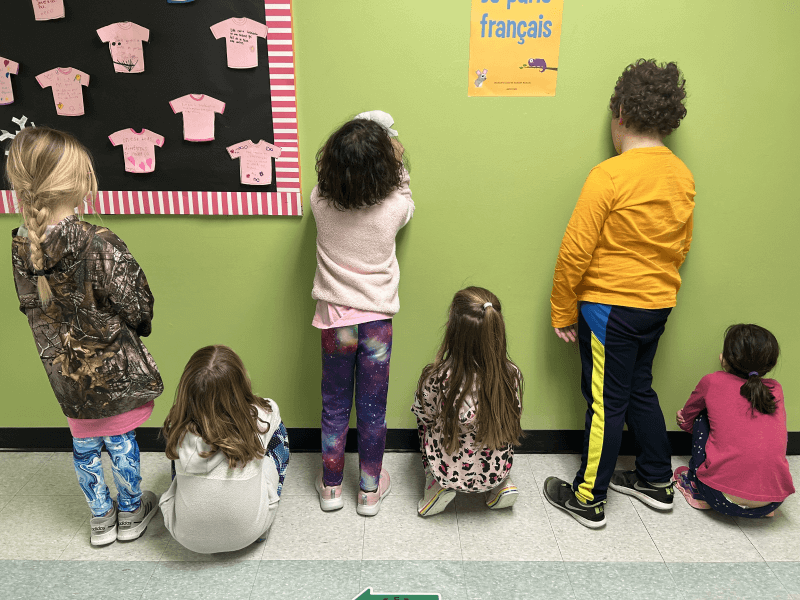
Dans la suite illustrée ci-dessus, l’attribut est la position : un élément accroupi et un élément debout bras tendus constituent le motif.
Note : Le changement de couleur est plus facile à reconnaître et à décrire lorsqu’une suite est construite avec du matériel concret, surtout en utilisant des objets qui ont tous la même forme, comme les perles d’un collier, les carreaux algébriques ou les cubes emboîtables.
- Changer l’attribut.
Explorer ensuite des suites ayant un autre attribut tel que la forme ou la grandeur, tout en ayant encore deux éléments dans le motif.
Exemple 1
Dans la suite illustrée ci-dessus, l’attribut est la forme. Les deux éléments, soit le voilier et le ballon, constituent le motif.
- Modifier la structure de la suite.
Explorer des suites plus complexes en ajoutant plus d’éléments au motif ou plus d’attributs. Les élèves feront alors face à un défi cognitif qui les mènera à un nouvel apprentissage.
Exemple 2
La suite ci-dessous comprend deux attributs, soit la forme et la couleur, et un motif à trois éléments, soit rectangle bleu, rectangle bleu, triangle orangé. Sa structure est AAB.
Poursuivre en introduisant une troisième forme ou couleur; par exemple, la suite ci-dessous comprend aussi deux attributs (forme et couleur) et un motif à trois éléments (rectangle bleu, triangle rouge, ovale jaune). Toutefois, sa structure est plus complexe, car il y a trois couleurs au lieu de deux et trois formes au lieu de deux. La structure de cette suite est ABC.
Note : Au début de la période de mathématiques, présenter des suites ayant des règles déjà explorées en salle de classe afin que les élèves les repèrent plus facilement et plus efficacement.
- Changer le mode de représentation.
Présenter des suites ayant la même structure, mais construites selon différents modes de représentation, puis vérifier si les élèves reconnaissent qu’elles ont la même structure. À titre d’exemple, présenter deux suites composées de matériel concret différent, comme une suite de perles et une suite de cubes emboîtables, ou, comme dans les photos ci-dessous, deux suites dont l’une est une représentation concrète (suite de positions) et l’autre, une représentation semi-concrète (suite d’objets dessinés). Lorsque les élèves peuvent justifier que les deux suites ont la même structure, elles et ils sont à un niveau d’abstraction plus élevé dans leur raisonnement algébrique.
- Explorer des suites ayant un élément manquant dans le motif.
Un défi intéressant à présenter aux élèves est l’identification d’un élément manquant dans le motif d’une suite.
Examiner la suite pour déterminer l’élément qui manque au début, au milieu ou à la fin d’un motif augmente leur compréhension des relations. Plusieurs explorations de ce genre aident les élèves à comprendre la suite comme un tout qui contient plusieurs motifs, plutôt que comme une séquence d’éléments changeants sans aucune relation.
Exemple 3
La perle manquante est une perle rouge.
- Repérer de fausses pistes.
Reconnaître qu’un attribut peut être une fausse piste dans une suite contribue au développement du raisonnement algébrique.
Exemple 4
Suite A :
Dans cette suite, les couleurs utilisées ne sont pas un attribut de la suite. Les élèves doivent donc éliminer l’attribut couleur et s’en tenir à l’attribut forme (triangle ou cercle).
Suite B :
Dans cette suite, les différentes formes et couleurs créent de fausses pistes qui doivent être éliminées afin de découvrir l’attribut, soit la position de la base (figure placée sur un côté plat ou sur un sommet).
Source : Guide d’enseignement efficace des mathématiques de la maternelle à la 3e année, p. 30-33.
Suites à motif croissant
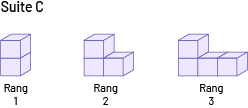
Les suites croissantes les plus simples sont celles dont la figure au rang 1 est composée d’un élément et dont chaque figure au rang subséquent n’augmente que d’un élément (exemple A). Les suites dont la figure au premier rang est composée de plus d’un élément et dont chaque figure au rang subséquent augmente d’un élément (exemple B) ou de plus d’un élément (exemple C) sont plus complexes.
Exemples
Lorsque les élèves construisent les figures d’une suite croissante selon une disposition rectangulaire, comme dans l’exemple C, elles et ils travaillent simultanément le concept de multiplication.
Source : Guide d’enseignement efficace des mathématiques de la maternelle à la 3e année, p. 40-41.
Suites numériques
Très tôt, les élèves prennent conscience des régularités dans leur environnement, dans la nature, dans les objets qui les entourent. C’est la raison pour laquelle il est possible de présenter les suites numériques dès la 1re année. Parallèlement, les élèves développent leur sens du nombre, peuvent compter par intervalles et à rebours et, par la suite, s’approprient le concept d’addition en tant que regroupement d’objets. Tous ces concepts ont un lien important avec l’apprentissage des régularités numériques.
« Puisque le système de numération est construit sur un système de régularités prévisibles, les élèves doivent non seulement être capables d’identifier les régularités qu’elles et ils voient, mais aussi de justifier leur raisonnement à l’aide de l’évidence qui explique la raison pour laquelle ces régularités existent. » [traduction libre] (Economopoulos, 1998)
Dès que les élèves commencent à explorer le système de numération à base 10, synonyme de système décimal, elles et ils découvrent qu’il y a répétition des chiffres de 0 à 9 lorsqu’elles et ils comptent au-delà de 9 (10, 11, 12, 13, 14, 15…). De voir et de justifier cette régularité dans le système décimal améliore la compréhension du sens du nombre et des regroupements (unités, dizaines, centaines, etc.). Par exemple, en comptant par bonds de 2, à partir de 16, les élèves observent une régularité prévisible dans les nombres 16, 18, 20, 22, 24, 26, 28, 30, 32… C’est un premier pas vers l’exploration des multiples de 2. Cette compréhension mène aussi à une capacité de compter à partir de tout nombre par n’importe quel bond. De même, lorsque les élèves comptent par 5, elles et ils reconnaissent rapidement une régularité, c’est-à-dire que le chiffre des unités alterne entre le chiffre 0 et le chiffre 5 (5, 10, 15, 20…). Elles et ils peuvent généraliser cette découverte informellement en disant que tout nombre qui est un multiple de 5 va se terminer par le chiffre 5 ou 0.
Tout comme lors de l’apprentissage des concepts relatifs aux suites non numériques, c’est en développant l’habileté à reconnaître, entre autres, des suites numériques avec une régularité d’addition et de soustraction que les élèves du cycle primaire construisent leur pensée algébrique. Les démarches décrites précédemment pour développer cette habileté s’appliquent aussi aux suites numériques.
Source : Guide d’enseignement efficace des mathématiques de la maternelle à la 3e année, p. 49-51.
Habileté : décrire les règles dans une variété de suites
Suites non numériques
Suites à motif répété
Pendant une activité, il importe que le personnel enseignant pose des questions pertinentes aux élèves afin de les amener à verbaliser leurs observations, à cerner les relations et à expliquer la façon dont elles et ils ont repéré la règle.
Afin d’aider les élèves à établir une compréhension intuitive de la structure de la suite, le personnel enseignant les encourage à verbaliser les éléments du motif qui se répète; par exemple, pour décrire la suite de mouvements claquer des doigts, claquer des doigts, lever le bras devant soi…, le personnel enseignant leur demande de dire tout haut : « claque, claque, lève… »; pour décrire une suite de perles formant un collier, il leur demande de toucher les perles en les nommant à voix haute : « perle bleue, perle mauve, perle rouge… » Lorsque les élèves décrivent leur suite, il est important d’expliquer la relation entre les motifs (les éléments du motif sont représentés dans le même ordre) et utiliser le vocabulaire mathématique approprié.
Exemples de questions
- Quels sont les attributs utilisés pour créer la suite?
- Quels sont les éléments du motif?
- Explique la raison pour laquelle c’est une suite.
À titre d’exemple, elles et ils peuvent décrire la suite illustrée ci-dessous comme suit : « Les attributs sont la forme et la position. Le motif est composé de trois éléments : un triangle pointant vers le haut, suivi d’un triangle pointant vers le bas, suivi d’un soleil. Les trois éléments du motif se répètent toujours dans cet ordre. »
Les élèves peuvent aussi laisser des traces pour montrer leur compréhension. Voici des exemples de traces :
image Suite, à motifs répétés de 3 éléments. Triangle qui pointe vers le haut, triangle qui pointe
vers le bas, soleil. En tout, il y a 9 éléments dans la suite. Ils sont numérotés de, un à 9, c’est le rang. Les
éléments sont aussi représentés par des lettres, « A », « B », « C », les lettres représentent la structure de la
suite. Un trait arrondi est placé sous chaque motif, ils représentent les vagues pour identifier chaque motif.La
régularité : les figures triangle pointant vers le haut, triangle pointant vers le bas, et soleil se répètent toujours
dans le même ordre.
Source : Guide d’enseignement efficace des mathématiques de la maternelle à la 3e année, p. 37-38.
Suites à motif croissant
En misant sur le changement des figures d’un rang à l’autre, les élèves décrivent la règle de façon informelle; par exemple, les élèves pourraient décrire la règle dans les suites ci-dessous comme suit :
Suite A :
« La règle de régularité est que l’on ajoute toujours une étoile à la figure au rang précédent. »
Suite B :
« La règle de régularité est que l’on ajoute toujours une rangée de trois carrés à la figure au rang précédent. »
Note : La suite est décrite en fonction du nombre d’éléments et non en fonction des attributs qui, eux, n’influencent pas la croissance de la suite.
Pour décrire la suite spécifiquement et voir les relations entre chaque rang, les élèves doivent aussi être en mesure de justifier la disposition des éléments qui composent chacune des figures. Le questionnement aide les élèves à développer leur habileté à raisonner et à reconnaître les relations. Afin de les aider, leur poser des questions telles que :
- Pouvez-vous expliquer comment on a réussi à construire la figure au 3e rang de la suite A? de la suite B?
- Comment sera construite la figure au 4e rang de la suite B? Que faut-il faire pour obtenir la figure au 5e rang de la suite A? de la suite B?
- À partir de quel rang avez-vous découvert une règle de régularité dans la suite A? dans la suite B?
Les élèves doivent explorer les suites croissantes en utilisant du matériel concret. Ensuite, les élèves discutent des façons de les créer ainsi que des relations qu’elles et ils voient. Les élèves expliquent aussi leur compréhension de la règle de régularité : « Chaque arbre est construit en ajoutant un rectangle au tronc de l’arbre précédent. »
Pour décrire la suite, les élèves peuvent aussi laisser des traces sur leurs travaux, comme dans l’exemple suivant.
L'âge de l'arbre et le nombre de formes pour le représenter chaque année.
Dans les suites croissantes, il existe aussi une relation entre le rang de chaque figure et le nombre d’éléments dans chacune. Cette relation est un concept mathématique très important, mis en évidence à l’aide d’une table de valeurs et menant à une généralisation plus formelle dès la 3e année, soit la formulation de la règle de correspondance.
Bien qu’en 1re année les élèves n’aient pas à définir la règle de correspondance, des discussions informelles traitant des relations entre les figures et le nombre d’éléments qui les composent peuvent avoir lieu en déterminant la règle de régularité et en prolongeant la suite.
L’étude des suites, qu’elles soient non numériques ou numériques, est la pierre angulaire de la compréhension des régularités. L’exploration des suites est un travail qui exige de la manipulation, des interventions et des discussions qui aideront chaque élève à faire un premier pas dans le monde algébrique.
Source : Guide d’enseignement efficace des mathématiques de la maternelle à la 3e année, p. 44-46.
Vocabulaire lié aux suites non numériques
Voici quelques notes explicatives sur le vocabulaire mathématique lié aux suites non numériques.
|
Suite non numérique : ensemble de figures ou d’objets disposés selon un ordre et une régularité. |
|
|
Suite à motif répété |
Suite à motif croissant |
 |
|
|
Attribut : caractéristique qui décrit un objet que l’on observe ou que l’on manipule. Dans la suite A, les attributs qui décrivent la suite sont la forme et la couleur. |
Dans une suite à motif croissant, l’analyse des attributs n’est plus importante, puisque l’accent est mis sur la croissance du motif. |
|
Terme : chaque figure, objet ou mouvement qui compose une suite non numérique. Dans la suite A, chacune des figures planes est un terme. |
Dans les suites B et C, chacune des figures est un terme. |
|
Motif : plus petite partie d’une suite à partir de laquelle est créée la régularité. Motif dans la suite A : un rectangle bleu suivi d’un trapèze vert et d’un triangle orangé. Chaque objet qui compose le motif est appelé élément du motif. |
Motif dans la suite B : un carré (figure au rang 1). Motif dans la suite C : deux cubes superposés (figure au rang 1). |
|
Règle : phénomène uniforme qui définit une suite et qui aide à déterminer chacun de ses termes. Règle de régularité dans la suite A : répétition du motif rectangle bleu, trapèze vert, triangle orangé, et ce, toujours dans le même ordre. |
Règle de régularité dans la suite B : un carré est ajouté à la figure précédente. Règle de régularité dans la suite C : un cube est toujours ajouté à la rangée du bas de la figure au rang précédent. |
|
Structure : représentation à l’aide de lettres de la règle d’une suite à motif répété. Dans la suite A, chaque élément du motif peut être identifié par une lettre : rectangle bleu (A), trapèze vert (B), triangle orangé (C). La structure de la suite A est donc ABC. |
|
|
Rang : position qu’occupe chaque terme dans une suite. Le rang est indiqué par un nombre. Il est utilisé pour aider à décrire les relations dans une suite et à prédire les prochains termes dans la suite sans devoir la prolonger. Dans la suite A, on trouve un rectangle bleu au 1er, au 4e et au 7e rang, un trapèze vert au 2e, au 5e et au 8e rang, etc. |
Dans les suites B et C, chaque figure a son rang : la première figure occupe le 1er rang, la deuxième figure occupe le 2e rang, etc. |
Source : Guide d’enseignement efficace des mathématiques de la maternelle à la 3e année, p. 29.
Suites numériques
Les démarches décrites précédemment pour décrire les suites non numériques s’appliquent aussi aux suites numériques.
Exemple
Suite C :
2, 4, 6, 8, 10
« La règle de régularité est que l’on ajoute toujours 2 au rang précédent. »
Vocabulaire lié aux suites numériques
Voici quelques notes explicatives sur le vocabulaire mathématique lié aux suites numériques.
Source : Guide d’enseignement efficace des mathématiques de la maternelle à la 3e année, p. 50.
Habileté : reconnaître et décrire des suites trouvées dans la vie quotidienne
Les jeunes enfants ont une curiosité et un intérêt naturels pour les régularités qui les entourent. Les régularités peuvent être de nature littéraire, artistique, musicale, scientifique ou numérique. On trouve des régularités dans bien des événements, comme la succession des saisons et des jours de la semaine, la croissance des êtres vivants et les activités quotidiennes; dans les comptines et les chansons, comme le rythme, les rimes et le nombre de syllabes; dans des histoires à structures répétées, comme le conte Boucle d’or et les trois ours; dans la musique, comme les différents sons d’instruments; dans des gestes, comme être debout, accroupi ou assis; et dans le monde que nous avons construit, comme les feux de circulation, les numéros de maison pairs ou impairs. Les motifs répétés décorant des objets, comme des vases, des vêtements et des bijoux, qui proviennent de diverses cultures sont aussi de bons exemples de régularités.
Source : Guide d’enseignement efficace des mathématiques de la maternelle à la 3e année, p. 26.