C2. Équations et inégalités :
Démontrer sa compréhension des variables, des expressions, des égalités et des inégalités, et mettre en application cette compréhension dans divers contextes.
Situation d’apprentissage : Quelles belles surprises!
Durée totale : 125 minutes
Sommaire
Dans cette situation d’apprentissage, les élèves représentent le contenu de deux sacs à surprises à l’aide de matériel semi-concret, de mots et de symboles. Elles et ils écrivent ensuite une phrase mathématique pour représenter les quantités d’objets dans ces sacs et vérifient si elle est vraie.
Note : Il est préférable de présenter cette activité lorsque vous commencez à représenter symboliquement des situations concrètes d’addition avec des phrases mathématiques.
| Attente | Contenus d'apprentissage |
|---|---|
| C2. Équations et inégalités Démontrer sa compréhension des variables, des expressions, des égalités et des inégalités, et mettre en application cette compréhension dans divers contextes. |
C2.2 Déterminer si des paires d’expressions numériques comportant des additions et des soustractions sont équivalentes ou non. C2.3 Déterminer et utiliser des relations d’équivalence comprenant des nombres naturels jusqu’à 50, dans divers contextes. |
Intention pédagogique
Le but de cette situation d’apprentissage est d’amener les élèves à :
- représenter des situations d’égalité de différentes façons;
- établir un lien entre les différentes représentations des quantités et les phrases mathématiques correspondantes.
| Contexte pédagogique | Préalables |
|---|---|
| La compréhension du concept d’égalité est essentielle au développement du raisonnement algébrique. Par conséquent, les élèves doivent expérimenter diverses situations dans lesquelles elles et ils s’exerceront à reconnaître, à définir, à créer et à établir une situation d’égalité.
Il importe de les amener à comprendre que le symbole de l’égalité, soit le signe =, qui se lit « est égal à », signifie que les nombres ou les expressions de chaque côté du signe = représentent la même quantité. En faisant appel aux connaissances antérieures des élèves, le personnel enseignant doit les inciter à explorer différentes représentations d’une même situation d’égalité. |
Pour être en mesure de réaliser cette situation d’apprentissage, les élèves doivent :
|
Matériel
- deux sacs à surprises contenant 10 objets chacun (le premier sac contenant trois types d’objets différents et le second, deux types d’objets différents)
- feuilles grand format (une par élève)
- cadres à 10 cases (deux par élève)
Vocabulaire mathématique
situation d’égalité, autant que, est égal à, n’est pas égal à, quantités égales, symbole de l’égalité, signe =, phrase mathématique
Avant l’apprentissage (mise en train)
Durée : environ 50 minutes
Présenter la situation aux élèves en disant :
J’ai trouvé chez moi deux sacs à surprises. J’ai écrit la lettre A sur le premier sac et la lettre B sur le second. Voyons ensemble ce que contient chaque sac.
Déposer devant les élèves les sacs A et B. Demander à une ou à un élève de sortir les objets du sac A et de les décrire. Demander à une ou à un autre élève de faire de même avec le sac B. Profiter de l’occasion pour présenter de nouveaux mots aux élèves, comme kaléidoscope et toupie.
Poser aux élèves la question suivante :
- Comment pourriez-vous disposer les objets de chaque sac à surprises afin de comparer le nombre d’objets de chaque sorte? » (En regroupant les objets identiques, comme illustrés dans les photos ci-dessous.)
Sac à surprises A :
4 toupies, 4 ballons et 2 jeux de cartes
Sac à surprises B :
6 kaléidoscopes et 4 jeux de cartes
- Combien d’objets de chaque sorte y a-t-il dans les sacs à surprises?
Demander aux élèves de suggérer un moyen de représenter le contenu des sacs à surprises sans utiliser les objets eux-mêmes ou sans recourir à des chiffres. La plupart des élèves suggéreront de dessiner les objets. Poursuivre la discussion afin de trouver d’autres représentations possibles.
Remettre à chaque élève une grande feuille de papier. Leur demander de tracer une ligne au centre de la feuille pour la diviser en deux, puis d’écrire « Sac à surprises A » et « Sac à surprises B » au haut de chaque section.
Demander aux élèves de représenter de différentes façons le contenu de chacun des sacs à surprises. Si elles et ils choisissent de dessiner les objets pour les représenter, souligner qu’il n’est pas nécessaire de s’attarder à l’exécution parfaite des dessins.
Circuler parmi les élèves et intervenir, au besoin, en leur posant des questions telles que :
- Tu as représenté les objets au moyen de dessins. Pourrais-tu maintenant les représenter autrement?
Voici quelques représentations en cours d’élaboration.
|
Modes de représentation |
Sacs à surprises A et B |
|
Dessins |
 |
|
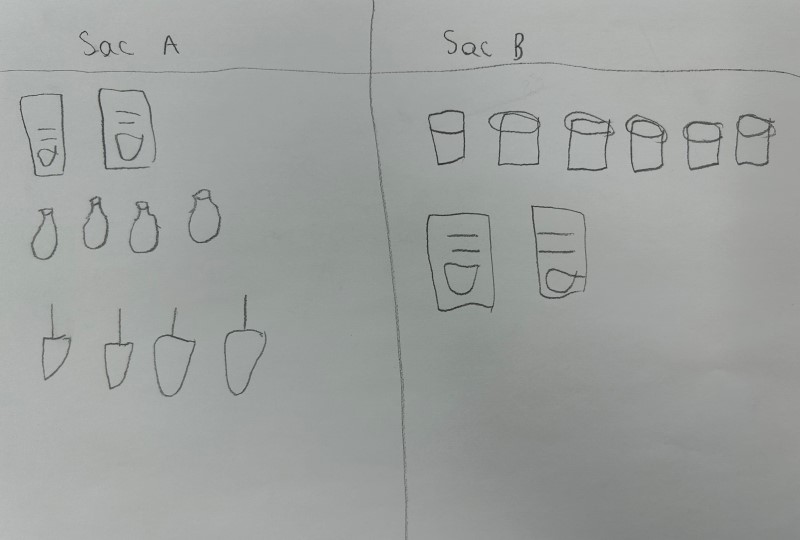Lettres |
Sacs à surprises A et B  |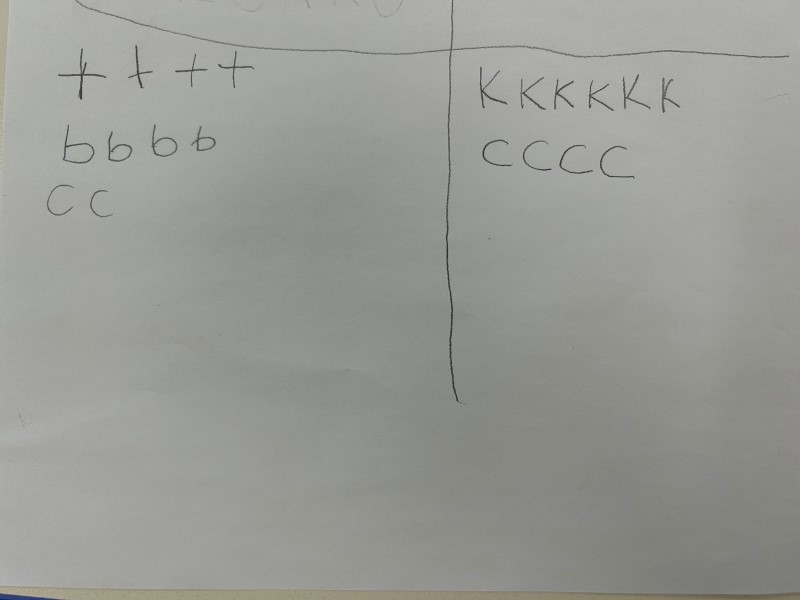
|
Mots et dessins |
 |
Inviter les élèves à présenter leurs représentations et à les expliquer, qu’elles soient conventionnelles ou non, puisqu’elles ont un sens pour elles et eux; par exemple, une élève indique qu’elle a choisi de représenter les quatre toupies par la lettre « D », puisqu’il s’agit de la 4e lettre de l’alphabet. Amener cette élève à comprendre l’inefficacité de sa représentation en lui demandant d’expliquer la façon dont elle symboliserait les quatre ballons.
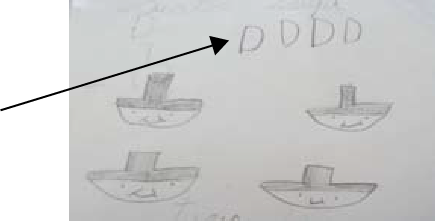
Une fois que les élèves auront terminé les différentes représentations, demander à des volontaires de les présenter aux autres. Leur poser des questions pour comparer les diverses représentations et établir des liens entre elles, telles que :
- Qu’est-ce qui est semblable entre la représentation avec des dessins et celle avec des lettres? entre la représentation avec des lettres et celle avec des mots? (Elles représentent les mêmes quantités d’objets.)
- Qu’est-ce qui est différent entre les représentations? (Le mode de représentation diffère, soit des dessins, des lettres ou des mots.)
Pendant l’apprentissage (exploration)
Durée: environ 45 minutes
Revoir avec les élèves le contenu de chaque sac à surprises et les représentations faites (dessins, mots, lettres) lors de la mise en train. Si le cadre à 10 cases n’a pas été utilisé pour représenter les quantités d’objets dans les sacs à surprises, proposer aux élèves de l’utiliser pour représenter les quantités d’objets dans le sac à surprises A.
Modeler l’exemple suivant : Je représente les quatre toupies dans le sac à surprises A en dessinant un point dans quatre des cases du cadre.
En utilisant le cadre à 10 cases, les élèves s’initient à une représentation plus symbolique d’une quantité d’objets, ce qui fait appel à leur capacité d’abstraction.
Remettre deux cadres à 10 cases à chaque élève et lui demander de représenter sur chacun le contenu d’un des sacs à surprises.
|
Observations possibles |
Interventions possibles |
|
Pour représenter les objets, les élèves les dessinent ou écrivent des mots ou des lettres dans chaque case du cadre.  |
Faire remarquer aux élèves qu’elles et ils ont déjà représenté les objets de cette façon sur leur feuille grand format. Inviter les élèves à proposer une façon plus efficace de représenter les objets dans leur cadre à 10 cases. Au besoin, rappeler aux élèves que les quantités peuvent être représentées dans un cadre à 10 cases à l’aide de points. |
|
Certaines et certains élèves utilisent une seule couleur pour représenter les différents objets dans le cadre à 10 cases. D’autres ajoutent la 1re lettre du nom de l’objet à côté de chaque point.  |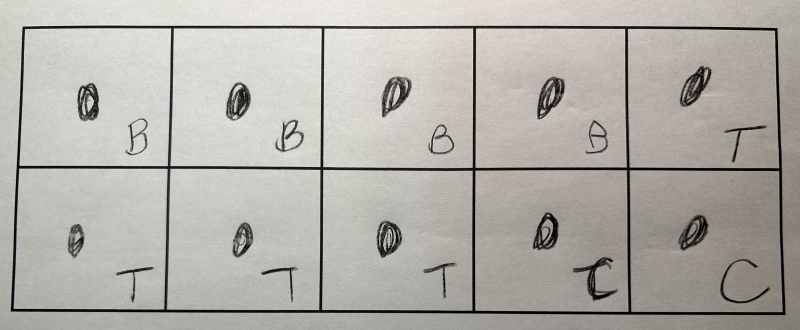
Inciter les élèves à utiliser une couleur différente pour chaque sorte d’objet en leur faisant remarquer qu’il est difficile de distinguer les sortes d’objets si ceux-ci sont tous représentés par la même couleur. Préciser que les points de couleur aident à voir plus aisément la quantité de chaque objet.   |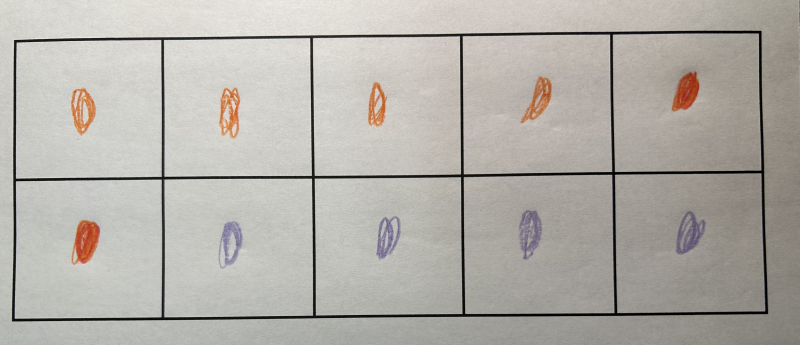
Présenter un des cadres à 10 cases dont les points représentent correctement le contenu du sac à surprises A. Inciter les élèves à établir le lien entre le nombre de points dans le cadre et la quantité d’objets dans le sac à surprises A en leur posant des questions telles que :
- Combien y a-t-il de points verts dans le cadre à 10 cases?
- Quels objets du sac sont représentés par les points verts? (les ballons, par exemple)
- Y a-t-il la même quantité de points que de ballons?
- Peux-tu les reconnaître dans le cadre à 10 cases?
- Combien de points y a-t-il en tout dans le cadre à 10 cases?
- Combien d’objets y a-t-il dans le sac à surprises A?
Faire remarquer aux élèves que le nombre de points dans le cadre à 10 cases est égal au nombre d’objets dans le sac à surprises A.
Présenter ensuite un cadre à 10 cases dont les points représentent correctement le contenu du sac à surprises B et reposer les mêmes questions afin d’établir de nouveau le lien entre le nombre de points dans le cadre et le nombre d’objets dans le sac.
Demander ensuite aux élèves de représenter la quantité d’objets dans chaque sac à surprises à l’aide de deux phrases mathématiques différentes. Une phrase mathématique est une expression symbolique qui représente une relation.
Voici quelques phrases mathématiques possibles pour chaque sac à surprises.
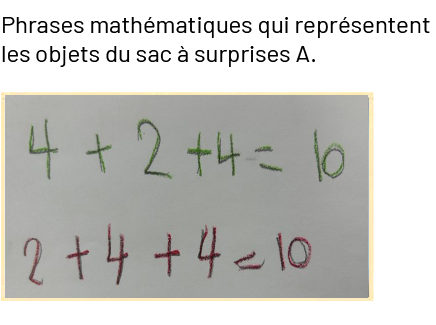
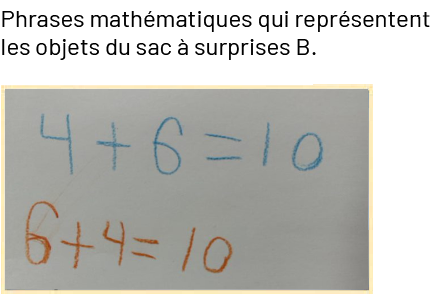
Source : Guide d’enseignement efficace des mathématiques de la maternelle à la 3e année, p. 135.
Il est important de représenter une même situation d’égalité par différentes phrases mathématiques. De cette façon, les élèves comprendront que le signe = ne sert pas uniquement à introduire une réponse à une opération; il exprime aussi la relation qui existe entre les nombres ou les expressions de chaque côté de ce signe.
|
Observations possibles |
Interventions possibles |
|
L’élève écrit des phrases mathématiques qui ne représentent pas les quantités d’objets contenus dans les sacs à surprises. |
Demander à l’élève ce que représentent les nombres dans ses phrases mathématiques. Inviter l’élève à dénombrer les toupies dans le sac à surprises A et d’écrire le nombre correspondant à cette quantité. Poursuivre ce questionnement pour les ballons et les jeux de cartes. Demander à l’élève de nommer le signe qu’elle ou il doit écrire pour indiquer que ces quantités sont rassemblées dans le même sac à surprises (le signe +) et le signe qu’elle ou il doit écrire pour indiquer que l’expression correspond à la somme de tous les objets rassemblés (le signe =). |
|
Des élèves omettent d’écrire les signes + ou =. |
Demander aux élèves de lire leurs phrases mathématiques à voix haute. Souligner qu’elles et ils ont dit plus et est égal à, mais que les symboles correspondants n’apparaissent pas dans leurs phrases mathématiques. Leur demander de les ajouter aux endroits appropriés. |
|
Des élèves n’écrivent qu’une seule phrase mathématique. |
Suggérer aux élèves de changer l’ordre dans lequel les objets ont été dénombrés et d’écrire une nouvelle phrase mathématique. |
Après l’apprentissage (objectivation/échange mathématique)
Durée: environ 30 minutes
Demander à une ou à un élève de présenter une de ses phrases mathématiques correspondant au contenu du sac à surprises A et d’expliquer la signification des symboles; par exemple, dans la phrase mathématique 4 + 4 + 2 = 10 :
- le premier 4 représente le nombre de ballons;
- le deuxième 4 représente le nombre de toupies;
- le 2 représente le nombre de jeux de cartes;
- le signe + représente la réunion des objets du sac à surprises A;
- le signe = signifie que les quantités représentées de chaque côté du signe sont égales.
Demander à une ou à un autre élève d’écrire et d’expliquer une phrase mathématique différente pour représenter les objets contenus dans le sac à surprises A. Si personne n’a trouvé une phrase différente, déplacer les jeux de cartes.
Demander ensuite à une ou à un élève de venir écrire une phrase mathématique qui représente cette autre situation, soit 2 + 4 + 4 = 10 ou 10 = 2 + 4 + 4.
Inciter les élèves à comparer les phrases 4 + 4 + 2 = 10 et 2 + 4 + 4 = 10 en posant des questions telles que :
- Les deux phrases mathématiques représentent-elles le contenu du sac à surprises A?
- Les deux phrases mathématiques sont-elles vraies? Comment le savez-vous?
Note : Cette question incite les élèves à vérifier si les expressions numériques de part et d’autre du signe représentent la relation qu’il indique (dans la situation présente, il s’agit du signe =). Si c’est le cas, on dit que la phrase mathématique est vraie.
Au besoin, suggérer à une ou à un élève de recourir à une des représentations ou aux objets contenus dans le sac à surprises pour le montrer.
Présenter d’autres phrases mathématiques ou demander à une ou à un élève de changer l’ordre des objets, d’écrire la phrase mathématique correspondante et de montrer la façon dont elle représente les objets du sac à surprises A.
Suivre la même démarche pour écrire les phrases mathématiques qui représentent le contenu du sac à surprises B; par exemple, selon l’objet choisi en premier (les kaléidoscopes ou les jeux de cartes), les phrases mathématiques pourraient être :
6 + 4 = 10
4 + 6 = 10
Si les élèves expliquent que les objets sont déjà réunis, elles et ils pourraient aussi écrire les phrases mathématiques :
10 = 4 + 6
10 = 6 + 4
Il est important de présenter les différentes phrases mathématiques qui représentent une même situation d’égalité afin d’aider les élèves à comprendre qu’une relation peut être représentée de différentes façons.
Poser ensuite aux élèves des questions liées aux représentations concrètes et symboliques du contenu des deux sacs à surprises telles que :
- Les deux sacs à surprises contiennent-ils une quantité égale d’objets? Comment le savez-vous? (Oui, puisque chaque sac contient 10 objets en tout.)
Pour chacun des sacs à surprises, choisir une phrase mathématique qui représente son contenu et combiner ces deux phrases pour en former une nouvelle; par exemple, combiner les phrases 2 + 4 + 4 = 10 et 6 + 4 = 10 pour former la phrase 2 + 4 + 4 = 6 + 4.
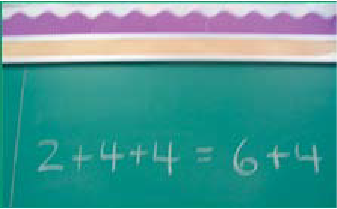
Écrire cette phrase au tableau et poser aux élèves des questions telles que :
- Les expressions numériques 2 + 4 + 4 et 6 + 4 sont-elles égales? Comment le savez-vous? (Parce que chacune représente le contenu d’un des sacs à surprises et que nous savons que chaque sac contient 10 objets.)
Lorsque les quantités des deux sacs à surprises sont comparées, la situation en est une d’équivalence.
Pour justifier l’égalité, certains élèves pourraient souligner les relations entre les nombres de chaque côté du signe = en disant : « Il y a un chiffre 4 de chaque côté du signe =. L’expression 2 + 4 qui se trouve du côté gauche est égale au 6 qui se trouve du côté droit. »
Prolongement : Nouvelles surprises!
Cette activité aide les élèves à approfondir le concept d’égalité en construisant diverses représentations d’une situation d’égalité donnée. La répétition de ce genre d’activité tout le long de l’année aide les élèves à considérer l’égalité comme une relation entre les expressions numériques situées de part et d’autre du signe =.
Mettre à l’avance 10 petits objets dans des sacs en plastique refermables en vous assurant d’inclure au moins quatre sortes d’objets différents dans chaque sac.
Former des équipes de deux. Remettre à chaque équipe un des sacs en plastique contenant 10 petits objets, une assiette en carton, une grande feuille et un cadre à 10 cases. Demander aux équipes de disposer le contenu de leur sac dans l’assiette et de représenter la quantité d’objets de différentes façons, comme elles et ils l’ont fait pour les sacs à surprises A et B lors de la situation d’apprentissage.
Voici quelques exemples de représentations possibles :
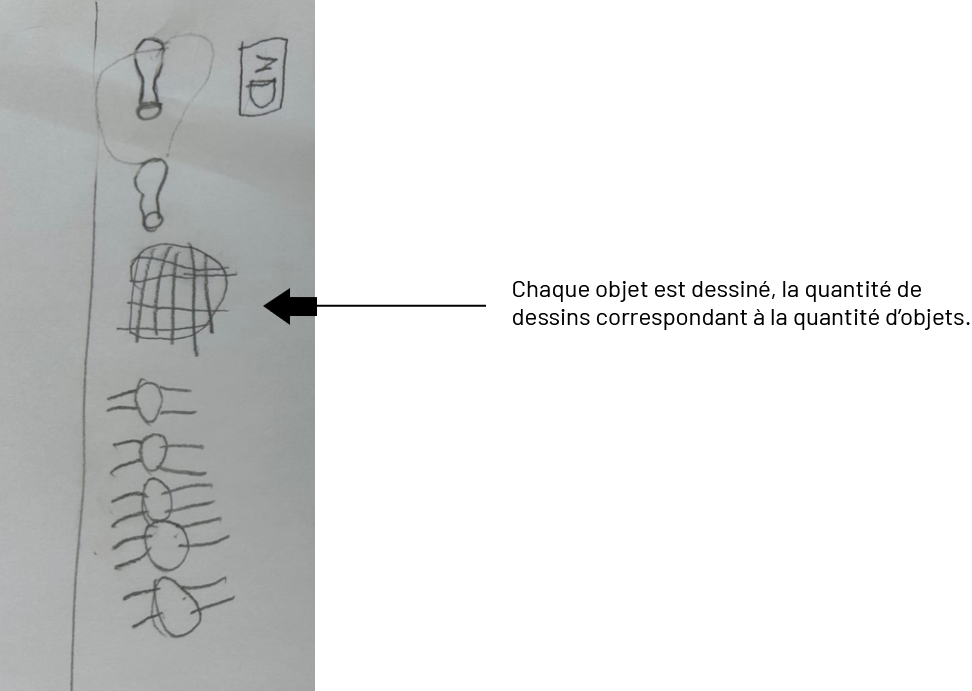
Un dessin dont les objets sont représentés par des lettres sous forme de suites. La légende se lit comme suit : « chaque objet est représenté par la première lettre de son nom, la quantité de lettres correspondant à la quantité d’objets ».« Le nom de chaque objet est écrit suivi du nombre représentant sa quantité. »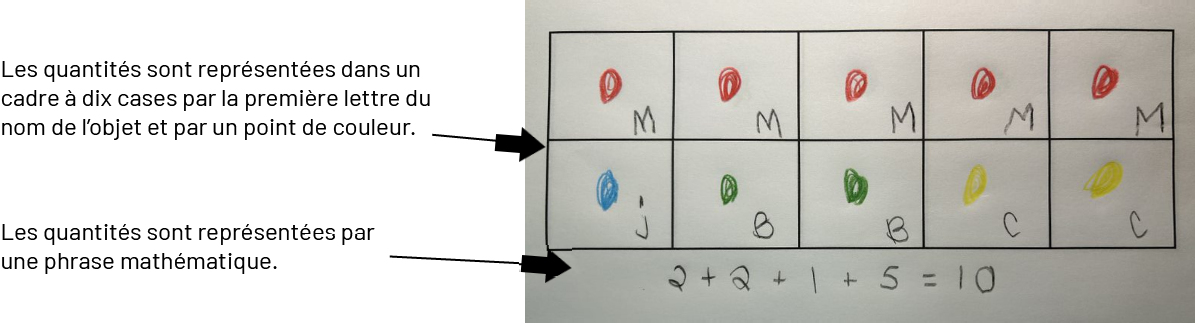
Cadre à dix cases. La légende se lit comme suit. « Les quantités sont représentées dans un cadre à dix cases par la première lettre du nom de l’objet et par une pointe de couleurs. » « Une flèche l'indique sur le graphique. En dessous, une autre flèche pointe vers une phrase mathématique et la légende se lit comme suit » « Les quantités sont représentées par une phrase mathématique.
Circuler et poser des questions
Inviter les élèves à faire part de leur raisonnement en leur posant des questions telles que :
- Pourquoi avez-vous regroupé les objets pareils? (Afin que les mêmes sortes d’objets soient plus faciles à dénombrer.)
- Comment représentez-vous les quantités de chaque sorte d’objet?
- En quoi vos représentations sont-elles semblables? En quoi sont-elles différentes?
- Quelle phrase mathématique pourrait représenter les quantités d’objets?
- Cette phrase mathématique est-elle vraie? Comment le savez-vous?
- Pouvez-vous écrire une autre phrase mathématique pour représenter les mêmes objets? Laquelle?
En groupe-classe, faire un retour sur les divers modes de représentation qu’utilisent les élèves en suivant le même genre de démarche et de questionnement utilisé lors de la situation d’apprentissage. S’assurer qu’elles et ils font le lien entre la représentation concrète et la phrase mathématique. Cibler les modes de représentation que n’ont pas utilisés les élèves afin de les expliquer de nouveau.
Comparer la phrase mathématique d’une des équipes, comme 2 + 2 + 1 + 5 = 10, avec la phrase mathématique qui représentait les objets contenus dans le sac à surprises B (4 + 6 = 10) et les écrire au tableau côte à côte.
Poser aux élèves des questions telles que :
- Qu’est-ce que les deux phrases mathématiques ont de similaire? (Les deux représentent une situation d’égalité comprenant 10 objets.)
- En quoi les deux phrases mathématiques diffèrent-elles? (L’une des phrases représente une situation d’égalité comprenant quatre sortes d’objets, tandis que l’autre représente une situation d’égalité comprenant deux sortes d’objets.)
- La phrase 2 + 2 + 1 + 5 = 4 + 6 est-elle vraie? Comment le savez-vous? (Elle est vraie, puisque les expressions numériques de chaque côté du signe = sont égales à 10.)
Différenciation pédagogique
La situation d’apprentissage peut être modifiée pour répondre aux différents besoins des élèves.
|
Pour faciliter la tâche |
Pour enrichir la tâche |
|
Demander aux élèves de représenter les situations d’égalité au moyen de dessins. S’assurer qu’elles et ils utilisent les expressions « est égal à » et « plus » lorsqu’elles et ils expliquent leur représentation. |
Demander aux élèves de créer des situations d’égalité semblables et de les présenter au groupe-classe. Inviter les élèves à écrire des phrases mathématiques afin qu’une ou un autre élève les illustre à l’aide de matériel concret. |
Suivi à la maison
Un membre de la famille décrit une situation possible d’équivalence ou d’égalité en utilisant le vocabulaire qu’a soumis le personnel enseignant. L’élève doit déterminer si l’énoncé est vrai ou faux et expliquer sa réponse. Voici deux suggestions d’énoncés :
- Le nombre de fenêtres dans la maison est égal au nombre de portes. (Il s’agit ici d’une situation possible d’équivalence.)
- Le nombre total de billes bleues et de billes rouges dans ta collection est égal à 18. (Il s’agit ici d’une situation possible d’égalité.)
Les élèves peuvent aussi jouer à représenter, à l’aide d’objets, des phrases mathématiques écrites sur des cartes; par exemple, un parent présente à son enfant une carte sur laquelle il a préalablement écrit 5 + 3 = 8 et lui demande de représenter la situation à l’aide de boutons ronds et de boutons carrés. (Il s’agit ici d’une situation d’égalité.)
Source : Guide d’enseignement efficace des mathématiques de la maternelle à la 3e année, p. 129-142.