C2.3 Déterminer et utiliser des relations d’équivalence comprenant des nombres naturels jusqu’à 100, dans divers contextes.
Activité 1 : exploration de propriétés
Explorer la propriété de commutativité
Exemple 1
Demander aux élèves de confectionner un collier en enfilant 5 perles rouges et 2 perles bleues, puis leur suggérer d’écrire la phrase mathématique correspondante.
(5 + 2 = 7)

Demander aux élèves de tourner le collier et d’écrire la phrase mathématique correspondante.
(2 + 5 = 7)

Proposer ensuite aux élèves de comparer les deux phrases mathématiques et de répondre aux questions suivantes :
- Que remarquez-vous au sujet de l’ordre des perles?
- Que remarquez-vous au sujet de la quantité de perles?
- Pourquoi la quantité est-elle la même dans les deux cas?
- Changez la quantité de perles sur le collier et écrivez deux phrases mathématiques. Comparez les phrases mathématiques. Que remarquez-vous?
- Si vous faites la même démarche en utilisant une grande quantité de perles sur le collier comme 100, 300 ou 500, que pouvez-vous affirmer au sujet des situations d’égalité que vous observez?
Note : Refaire l’activité en demandant aux élèves de se déplacer pour observer le collier dans l’autre direction au lieu de le tourner.
Exemple 2
Demander aux élèves de déterminer si les phrases mathématiques ci-dessous sont vraies ou fausses sans effectuer de calcul.
6 + 3 = 3 + 6
45 + 34 = 34 + 46
67 + 89 = 89 + 67
3 × 8 = 8 × 2
Après leur avoir présenté chaque phrase mathématique, poser aux élèves les questions suivantes :
- Comment pouvez-vous affirmer que cette phrase est vraie ou fausse?
- Que remarquez-vous au sujet des termes de cette égalité?
Explorer le rôle du nombre 0 dans l’addition
Présenter aux élèves six jouets et leur demander de les dénombrer. Recouvrir les jouets d’un tissu et préciser que vous allez ajouter un nombre mystère de jouets.

Faire semblant d’ajouter des jouets, mais ne rien ajouter. Retirer le tissu et poser aux élèves les questions suivantes :
- Combien y a-t-il de jouets maintenant?
- Combien de jouets ai-je ajoutés?
Demander aux élèves d’écrire une phrase mathématique pour représenter la situation. (6 + 0 = 6)
Refaire l’activité en ajoutant 6 jouets à 0 jouet afin de représenter 0 + 6 = 6.
Faire remarquer que, puisque 6 + 0 = 6 et que 0 + 6 = 6, on peut conclure que 6 + 0 = 0 + 6 en faisant le lien avec la propriété de commutativité de l’addition.
Encourager les élèves à proposer une conjecture sur le rôle du nombre 0 dans une addition, puis leur poser des questions telles que :
- Pourriez-vous appliquer votre conjecture à d’autres nombres? Essayez.
- Pourriez-vous appliquer votre conjecture à tous les nombres? Pourquoi?
Explorer le rôle du nombre 0 dans la soustraction
Demander aux élèves d’écrire une phrase mathématique pour représenter la situation. (8 – 0 = 8)
Encourager les élèves à proposer une conjecture sur le rôle du nombre 0 dans une soustraction, puis leur poser des questions telles que :
- Pourriez-vous appliquer votre conjecture à d’autres nombres? Essayez.
- Pourriez-vous appliquer votre conjecture à tous les nombres? Pourquoi?
Explorer le rôle du nombre 1 dans la multiplication
Présenter aux élèves une assiette contenant huit billes (ou autres objets, comme des jetons, des boutons, des cubes) et leur demander de les dénombrer.

Souligner le fait qu’il s’agit d’un groupe de huit billes et écrire la phrase mathématique correspondante :
1 × 8 = 8
Répéter l’activité en utilisant des ensembles comportant huit éléments différents (par exemple, un groupe de huit élèves, un groupe de huit crayons).
Faire remarquer que 1 × 8, c’est toujours égal à 8.
Reprendre la même activité en utilisant d’autres nombres.
Présenter ensuite aux élèves une activité comportant huit groupes d’un élément (par exemple, huit élèves ont chacun une bicyclette) afin de représenter 8 × 1 = 8.
Faire remarquer que, puisque 1 × 8 = 8 et que 8 × 1 = 8, on peut conclure que 1 × 8 = 8 × 1 en faisant le lien avec la propriété de commutativité de la multiplication.
Encourager les élèves à proposer une conjecture sur le rôle du nombre 1 dans une multiplication, puis leur poser des questions telles que :
- Pourriez-vous appliquer votre conjecture à d’autres nombres? Essayez.
- Pourriez-vous appliquer votre conjecture à tous les nombres? Pourquoi?
Explorer la propriété d’associativité
Exemple 1

Présenter aux élèves trois wagons de train construits avec des cubes emboîtables de différentes couleurs.

Proposer aux élèves d’aider M. Bontrain, le chef de train, qui désire regrouper deux wagons sans en modifier l’ordre.
Représenter chaque situation possible à l’aide des cubes et écrire la phrase mathématique correspondante. Afin d’éviter d’avoir recours aux parenthèses, utiliser des encadrés pour illustrer les wagons.
Note : Les wagons peuvent être regroupés de deux façons :

Poser aux élèves les questions suivantes :
- Y a-t-il d’autres regroupements possibles de wagons? Comment le savez-vous?
- Quelle est la somme des cubes qui forment le train dans chaque cas?
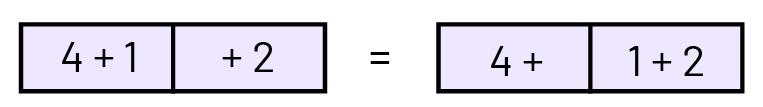 Des
boîtes représentant des wagons pour illustrer une équation équilibrée. Sur le côté gauche, une boîte montre l’équation
« 4 » « plus » « un ». La boîte voisine indique « plus » « 2 ». « Égal ». Une boîte contenant « 4 » « plus ». Elle est
collée à une deuxième boîte contenant l'équation « un » « plus » « 2 ».
Des
boîtes représentant des wagons pour illustrer une équation équilibrée. Sur le côté gauche, une boîte montre l’équation
« 4 » « plus » « un ». La boîte voisine indique « plus » « 2 ». « Égal ». Une boîte contenant « 4 » « plus ». Elle est
collée à une deuxième boîte contenant l'équation « un » « plus » « 2 ».
- Comment est-ce possible que la somme reste pareille même si nous avons différents regroupements de wagons?
- Est-ce que cela fonctionnerait en utilisant trois autres nombres? Démontrez-le à l’aide d’une droite numérique ouverte double et d’une phrase mathématique. »
Demander aux élèves d’expliquer à une personne leur observation.
Par la suite, poser aux élèves la question suivante :
- Que pourriez-vous écrire dans votre journal mathématique collectif au sujet de ce que vous avez découvert aujourd’hui?
Reprendre l’activité en utilisant un plus grand nombre de wagons.
Note : Les élèves qui connaissent la propriété de commutativité, pourraient modifier l’ordre des termes à additionner (par exemple, 4 + 2 + 1). Si tel est le cas, leur demander de justifier la raison pour laquelle il est possible de modifier l’ordre. Sinon, leur mentionner simplement que l’ordre des wagons ne peut être modifié, puisqu’ils sont attachés ainsi sur la voie ferrée.
Exemple 2
Demander aux élèves de vérifier l’égalité des phrases mathématiques ci-dessous sans effectuer de calcul.
(7 + 4) + 6 = 7 + (4 + 6)
46 + (34 + 67) = 46 + (34 + 46)
67 + (89 + 103) = (67 + 89) + 105
Pour chaque phrase, poser aux élèves des questions telles que :
- Comment pouvez-vous affirmer que cette phrase est vraie (ou fausse)?
- Que faut-il faire pour rendre cette phrase vraie?
Source : Guide d’enseignement efficace des mathématiques de la maternelle à la 3e année, p. 90-100.
Activité 2 : utilisation de stratégies pour développer la pensée algébrique
Ajouter un nombre mystère
Grouper les élèves en équipes de deux. Leur demander de construire deux tours composées de six cubes emboîtables chacune.
Poser aux élèves la question suivante :
- Que remarquez-vous en observant les deux tours?
Leur demander d’ajouter, au choix, un certain nombre de cubes aux tours tout en s’assurant de maintenir l’égalité.
Demander à chaque équipe d’expliquer la façon dont elle a maintenu l’égalité. Écrire ensuite les réponses dans un tableau.
Exemple
| Groupe | Hauteur des tours au début | Ajout par l’élève A | Ajout par l’élève B |
|---|---|---|---|
| 1 | 6 | 3 | 3 |
| 2 | 6 | 4 | 4 |
| 3 | 6 | 1 | 1 |
| 4 | 6 | 5 | 5 |
| 5 | 6 | 2 | 2 |
Demander aux élèves d’analyser les données. Attirer leur attention sur le fait que la même quantité doit être ajoutée à chacune des tours pour que l’égalité soit maintenue. Leur faire remarquer que cette constatation est vraie pour toutes les quantités ajoutées.
Demander aux élèves de vérifier s’il est possible d’ajouter une quantité à une seule tour et de maintenir l’égalité. Leur faire remarquer que l’égalité se maintient seulement si rien n’est ajouté (0 cube).
Demander à un membre de chaque équipe d’ajouter un cube à sa tour, puis poser aux élèves les questions suivantes :
- Que remarquez-vous maintenant en observant les deux tours?
- Que devez-vous faire pour rétablir l’égalité?
Note : Les élèves doivent être en mesure de constater et d’expliquer l’inégalité avant de chercher à rétablir l’égalité.
Demander à un membre de chaque équipe d’ajouter, au choix, de 2 à 5 cubes à sa tour.
Inviter l’autre membre à rétablir l’égalité entre les deux tours.
Demander à chaque équipe d’expliquer la façon dont elle a rétabli l’égalité. Faire remarquer aux élèves que chaque équipe a dû ajouter à la deuxième tour la même quantité de cubes que celle ajoutée à la première tour pour rétablir l’égalité. Attirer leur attention sur le fait que cette constatation s’applique à toutes les quantités ajoutées.
Décomposer les nombres selon les valeurs de position
Présenter aux élèves les phrases mathématiques ci-dessous et leur demander si elles sont vraies ou fausses :
47 = 40 + 7
35 + 12 = 35 + 10 + 2
47 + 21 = 40 + 20 + 7 + 1
700 + 90 + 5 + 8 = 795 + 8
Afin d’inciter les élèves à justifier leurs réponses, leur poser les questions suivantes :
- Comment pouvez-vous affirmer que cette phrase mathématique est vraie (ou fausse)?
- Est-ce possible de vérifier l’égalité à l’aide de matériel concret (par exemple, cadres à dix cases, matériel de base dix, cubes emboîtables)?
- Comment ce matériel aide-t-il à déterminer si la phrase est vraie (ou fausse)?
- Est-ce possible de vérifier l’égalité sans matériel concret et sans effectuer de calcul? Comment?
Annuler des termes ou des expressions égales
Exemple 1
Écrire la phrase mathématique suivante : 6 + 24 + 32 = 32 + 24 + 6
Poser aux élèves les questions suivantes :
- Cette phrase mathématique est-elle vraie ou fausse? Comment le savez-vous? (Des élèves recourront à la commutativité.)
- Si j’enlève les nombres 32 de chaque côté du signe d’égalité, l’égalité demeure-t-elle vraie?
- Si j’enlève les nombres 24 de chaque côté du signe d’égalité, l’égalité demeure-t-elle vraie?
Écrire la phrase mathématique suivante : 6 + 24 + 32 = 32 + 20 + 4 + 7
Poser aux élèves les questions suivantes :
- Cette phrase mathématique est-elle vraie ou fausse?
- Comment le savez-vous?
Exemple 2
Présenter aux élèves les phrases mathématiques ci-dessous et leur demander de vérifier si elles sont vraies ou fausses :
3 + 4 + 2 = 3 + 3 + 2
5 + 6 + 8 = 6 + 5 + 8
11 + 7 + 4 = 5 + 6 + 7 + 4
54 + 67 + 75 = 54 + 67 + 75
12 + 78 + 20 + 3 = 78 + 23 + 14
Pour chaque phrase mathématique, poser aux élèves les questions suivantes :
- Cette phrase est-elle vraie ou fausse?
- Si vous annulez des termes qui sont pareils de chaque côté du signe d’égalité, l’égalité demeure-t-elle vraie? Comment le savez-vous?
Comparer des termes
Présenter aux élèves les phrases mathématiques suivantes :
9 + 8 = 10 + 7
34 + 67 = 35 + 66
23 + 48 = 26 + 45
Demander aux élèves de vérifier, à l’aide d’une droite numérique ouverte double, si ces phrases sont vraies.
Pour chaque phrase, poser aux élèves les questions suivantes :
- Comment pouvez-vous affirmer que cette phrase est vraie?
- Quels termes avez-vous comparés?
- Que remarquez-vous au sujet de ces termes?
- Pouvez-vous comparer les termes d’une autre façon?
Source : Guide d’enseignement efficace des mathématiques de la maternelle à la 3e année, p. 101-108.
Activité 3 : représenter des quantités pour comprendre les relations d’équivalence
Lorsque les nombres sont décomposés, les parties sont équivalentes à leur tout.
Les différentes activités ci-dessous aident les élèves à comprendre que, même si la quantité est décomposée de
différentes façons, elle reste la même (par exemple, 50 = 25 + 25; 49 + 1 = 1 + 49; 20 + 20 = 10 + 10 + 10 + 10). Les
représentations concrètes et semi-concrètes peuvent, par la suite, être associées à une représentation symbolique.
Représenter 90 cents ou 90 dollars de diverses façons à l’aide de différentes pièces de monnaie ou de billets
factices. Si vous n’avez pas assez de matériel pour l’ensemble des élèves, utiliser le site Web ontarien mathies.
Représenter 75 à l’aide de différents bonds sur une droite numérique ou sur une droite perlée.
Nombre mystère : Grouper les élèves en équipes de deux. Leur demander de représenter un nombre de différentes façons (matériel concret, semiconcret, symboliquement). Inviter les élèves à circuler dans la salle de classe afin de voir la façon dont les autres équipes ont représenté leur nombre mystère.
Activité 4 : une histoire d’ajout, de réunion et de comparaison!
Sommaire
Dans cette activité, les élèves créent et représentent trois situations différentes qui correspondent à une même phrase mathématique donnée. Il s’agit d’une situation d’ajout, d’une situation de réunion et d’une situation de comparaison.
Déroulement
Présenter aux élèves une phrase mathématique comportant une addition (par exemple, 7 + 2 = 9).
Créer et représenter, à l’aide de matériel de manipulation, trois situations qui correspondent à la phrase mathématique : une situation d’ajout, une situation de réunion et une situation de comparaison.
Décrire chaque situation à l’aide de mots.
Exemple
Situation d’ajout
Dans mon sac, j’ai 7 cartes de joueurs de hockey. J’ajoute 2 autres cartes dans mon sac. J’ai maintenant 9 cartes en tout dans mon sac.
Situation de réunion
Pour une présentation en classe, j’apporte 7 cartes de joueurs de hockey et mon amie apporte 2 cartes. Nous regroupons nos cartes pour en avoir 9 à présenter.
Situation de comparaison
Sur mon pupitre, il y a mes 7 cartes de joueurs de hockey et les 2 cartes de mon amie. Un autre ami a, sur son pupitre, 9 cartes de joueurs de baseball. Nous constatons que nous avons le même nombre de cartes.
Note : La situation d’ajout et la situation de réunion sont des exemples de situations d’égalité, alors que la situation de comparaison est un exemple de situation d’équivalence.
Mettre du matériel de manipulation à la disposition des élèves. Grouper les élèves en équipes de deux. Remettre à chaque équipe une carte sur laquelle est écrite une phrase mathématique comportant une addition.
Demander à chaque équipe de créer et de représenter, à l’aide de matériel de manipulation, trois situations qui correspondent à cette phrase (une situation d’ajout, une situation de réunion et une situation de comparaison) et de décrire chacune à l’aide de mots.
Inviter quelques équipes à présenter leurs trois situations et demander aux autres élèves d’identifier la situation d’ajout, la situation de réunion et la situation de comparaison.
Source : Guide d’enseignement efficace des mathématiques de la maternelle à la 3e année, p. 165-166.
