C2.1 Décrire des façons et des situations où des symboles sont utilisés comme variables.
Habileté : décrire des façons et des situations où des symboles sont utilisés comme variables
Symboles de la vie courante
Très jeunes, les élèves évoluent dans un monde où les signes omniprésents communiquent, par leur nature, un message clair ou définissent une fonction précise; par exemple :
- les feux de signalisation dictent un comportement (le rouge, un arrêt ou une interdiction d’avancer; le vert, l’autorisation d’avancer);
- les personnages sur les portes des salles de toilettes renseignent sur la porte à choisir;
- à la garderie, plusieurs symboles indiquent où ranger les jouets, les vêtements, etc.;
- une chanson ou une comptine annonce une activité spécifique (par exemple, le temps de la collation, du repos, du rangement);
- les signes de sécurité de SIMDUT, qu’enseignent souvent les parents, sensibilisent les enfants à la toxicité des produits de nettoyage;
- les panneaux routiers, les logos et les enseignes commerciales deviennent rapidement significatifs pour les enfants.
L’acquisition de ces symboles se fait par l’expérience, sans que les symboles soient systématiquement enseignés, mémorisés ou récités. Malgré leur nature arbitraire, les symboles deviennent rapidement familiers aux enfants. Ainsi, chaque symbole utilisé dans un contexte donné est associé à un sens spécifique, et cette association ne sera plus contestée. Cependant, ils peuvent donner lieu à d’autres interprétations s’ils sont utilisés dans de nouveaux contextes.
Symboles mathématiques
Les symboles mathématiques représentent des concepts fondamentaux sur lesquels s’appuie l’apprentissage des mathématiques et de l’algèbre. Plusieurs d’entre eux, devenus familiers aux adultes, sont souvent présentés aux élèves de manière prématurée dans des situations hors contexte ou sans explications au préalable. Il est donc essentiel, pour les expliquer clairement et précisément, de créer des situations dans lesquelles les élèves auront le loisir et le temps de se familiariser avec les symboles et de s’approprier leur sens.
| Symboles mathématiques | Exemples |
|---|---|
| Les symboles désignant des quantités Les chiffres (symboles numériques ou graphiques indo-arabes) |
0, 1, 2, 3, 4, 5, 6, 7, 8, 9 |
| Les symboles représentant des opérations fondamentales Les signes qui désignent les quatre opérations en numération |
– + × ÷ |
| Les symboles établissant des relations Le signe qui indique une égalité Les signes qui indiquent une inégalité |
= ≠ > < |
Source : Guide d’enseignement efficace des mathématiques de la maternelle à la 3e année, p. 52.
Sens du symbole en algèbre
À mesure qu’ils vivent des expériences variées et significatives, les élèves acquièrent le sens du symbole. Le sens du symbole est un niveau de compréhension mathématique qui englobe le sens du nombre
(H. Picciotto et A. Wah, « A New Algebra: Tools, Themes, Concepts », Journal of Mathematical Behaviour, vol. 12, no 1, 1993, p. 42, traduction libre, cités dans ministère de l’Éducation de l’Ontario, Guide d’enseignement efficace des mathématiques, de la maternelle à la 3e année – Modélisation et algèbre, fascicule 2, 2008, p. 65).
Luis Radford (2001) considère l’apprentissage de l’algèbre comme l’appropriation d’une nouvelle manière mathématique de penser et d’agir où s’insèrent la production et l’utilisation de symboles. Ces symboles sont porteurs de sens pour les élèves dans la mesure où ils sont explorés dans des activités mathématiques contextualisées.
Un des éléments clés du raisonnement algébrique repose sur la capacité à reconnaître et à explorer les relations qui lient diverses quantités. Ces relations sont représentées par divers symboles que les élèves doivent apprendre à utiliser de façon appropriée.
Au cycle primaire, un tiret, une figure géométrique ou tout autre symbole dans une équation représente, pour les élèves, une quantité inconnue (par exemple, dans l’équation 3 + Δ = 5, le triangle est un symbole qui représente la quantité 2). L’utilisation adéquate d’une case ou d’un tiret est une première étape vers le symbolisme plus formel de l’algèbre.
Les élèves qui en auront une compréhension juste sauront, au cycle moyen, interpréter ou manipuler plus efficacement les symboles littéraux utilisés couramment en algèbre pour représenter la variable. Le sens du symbole joue un rôle important dans le développement de la pensée algébrique. La compréhension des symboles découle de la maturité des élèves et de la diversité des expériences vécues.
Voici quelques points à considérer pour aider les élèves à développer le sens du symbole :
- Présenter aux élèves les symboles dans des contextes stimulants et réalistes pour leur permettre d’en saisir le sens et, ultimement, de comprendre les concepts qu’ils sous-tendent.
- Inciter les élèves à déterminer les éléments à représenter dans une situation-problème, à choisir un mode de représentation adéquat et à utiliser des symboles personnels.
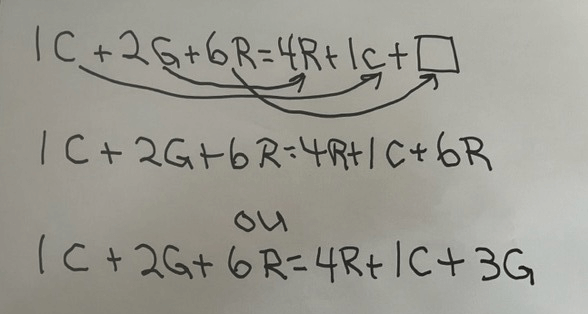 Image L'élève construit une expression mathématique avec une variable vide à remplir. L'élève a
démontré son raisonnement à l'aide de flèches et propose ensuite deux énoncés possibles pour justifier son
raisonnement.
Image L'élève construit une expression mathématique avec une variable vide à remplir. L'élève a
démontré son raisonnement à l'aide de flèches et propose ensuite deux énoncés possibles pour justifier son
raisonnement.
Ci-dessus, les élèves utilisent la première lettre du nom de chaque animal pour formuler la phrase mathématique; par exemple, C représente le crapaud, G représente la grenouille et R représente la rainette.
Encourager les élèves à déterminer le moment et la façon d’utiliser des symboles (par exemple, représenter une quantité manquante, dans une équation, par un carré).
Proposer aux élèves des activités qui les amènent à créer des liens entre divers modes de représentation, à discuter de ces liens et à les justifier à l’aide d’arguments mathématiques.
Pour développer le sens du symbole, les élèves doivent :
- décrire des relations à l’aide de divers modes de représentation avant de les explorer symboliquement;
- établir des liens entre les représentations.
Source : Guide d’enseignement efficace des mathématiques de la maternelle à la 3e année, p. 51-54.
Il importe également d’amener les élèves à observer qu’il y a des quantités qui ne changent pas dans leur vie quotidienne. Cette prise de conscience les aidera à mieux saisir le concept de constante plus tard dans leurs apprentissages. Le fait de trouver, dans leur vie de tous les jours, des quantités qui restent les mêmes et des quantités qui peuvent changer aidera les élèves à comprendre le concept de variable.
Source : Curriculum de l’Ontario, Programme-cadre de mathématiques de la 1re à la 8e année, 2020, Ministère de l’Éducation de l’Ontario.
L’utilisation efficiente de différents modes de représentation s’inscrit comme un cheminement progressif intégré au domaine Nombres. Son but dépasse de loin le simple recours mécanique aux symboles et aux « trucs » de mémorisation en algèbre. Ce cheminement consiste plutôt à développer la capacité à percevoir des régularités, à généraliser des relations et à résoudre des problèmes.
Voici un exemple de situation-problème authentique illustrant un cheminement progressif vers le développement du sens du symbole.
| Cheminement pour développer le sens du symbole | Exemples |
|---|---|
| Exposer la situation et les données. | L’élève pourrait exposer la situation suivante : Dans l’autobus, il y a 10 personnes après le premier arrêt et 15 personnes après le deuxième arrêt. Combien de personnes sont montées dans l’autobus au deuxième arrêt et combien en sont descendues? |
| Proposer une conjecture | Je crois que le nombre de personnes qui descendent de l’autobus est toujours plus petit que le nombre de personnes qui montent dans l’autobus. |
| Représenter la situation-problème à l’aide de matériel concret ou de dessins. | Les élèves utilisent des cubes pour représenter les personnes.

Les élèves représentent les personnes à l’aide de dessins. 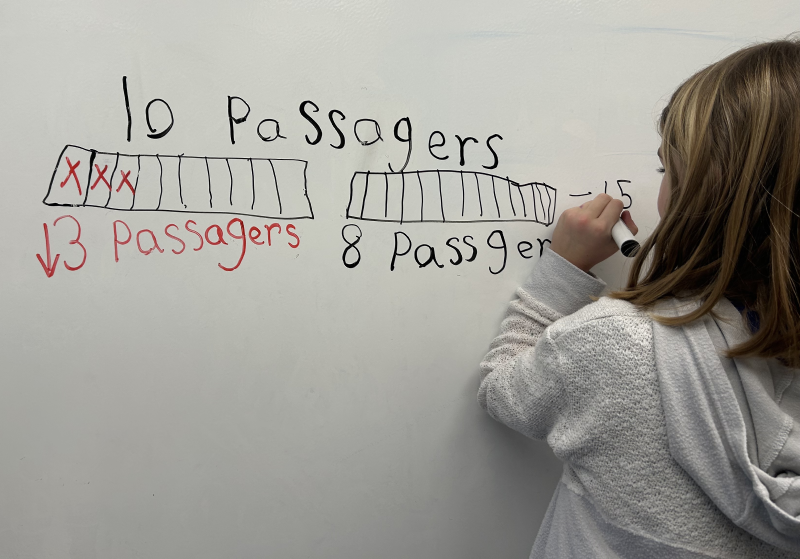
|
| Délaisser graduellement les représentations semi-concrètes et utiliser des symboles personnels pour communiquer sa compréhension de la situation. | Dans la photo ci-dessous, l’élève a choisi les symboles suivants comme étiquettes :
p pour personnes; d pour les personnes qui descendent de l’autobus; m pour les personnes qui montent dans l’autobus. 
|
Pour développer le sens de l’inconnue, les élèves doivent explorer une variété de situations authentiques qui font appel à des données signifiantes et qui favorisent la transition du concret vers l’abstrait.
Source : Guide d’enseignement efficace des mathématiques de la maternelle à la 3e année, p. 54-55.
Les symboles peuvent être employés pour représenter et décrire, de façon abstraite, la suite créée dans un mode concret ou semi-concret.
Par exemple, les élèves utilisent une représentation semi-concrète pour illustrer une suite de briques placées à la verticale et à l’horizontale.
Exemple
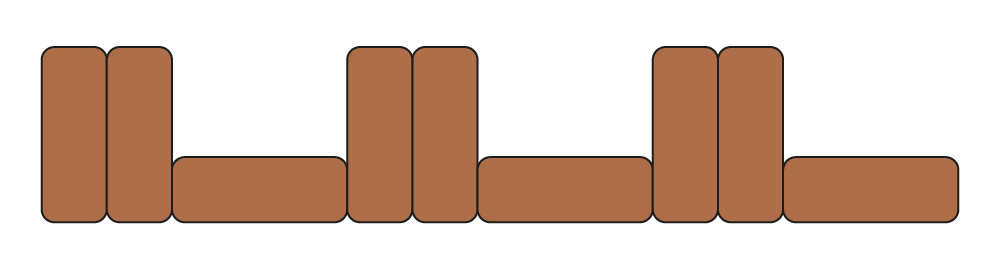
Les élèves comprennent rapidement que c’est très long de dessiner les briques et décident alors, à la suite de cette constatation, d’utiliser des symboles tels que D (debout) et C (couchée) pour représenter les éléments brique debout et brique couchée dans la suite et décrire sa structure.
En utilisant des symboles significatifs pour eux, les élèves approfondissent leur compréhension d’une représentation symbolique. Les symboles deviennent alors un moyen efficient de représenter la situation et la régularité observée.
Exemple

Un modèle utilisant des blocs. Le modèle est composé de deux blocs en position verticale et d'un bloc en position horizontale. Ce motif est répété trois fois.
En dessous des blocs se trouvent des lettres. Le motif est « D », « D », « C » répété 3 fois.
Source : Guide d’enseignement efficace des mathématiques de la maternelle à la 3e année, p. 17.
Connaissance : symbole
Signe graphique qui représente un nombre, une opération, une relation.
Note : Dans une équation, si le même symbole apparaît plus d’une fois, sa valeur est identique, Par exemple, 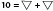 . Deux symboles différents
dans une équation peuvent avoir des valeurs variées. Par exemple,
. Deux symboles différents
dans une équation peuvent avoir des valeurs variées. Par exemple, 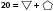 , les deux symboles peuvent
avoir des valeurs de 10 et 10, 19 et 1, etc.
, les deux symboles peuvent
avoir des valeurs de 10 et 10, 19 et 1, etc.
Connaissance : variable
Un terme (symbole ou lettre), dans une équation, qui peut être remplacé par une ou plusieurs valeurs.
Dans l’équation 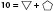 Ou 10 = x
+ y, les formes ou les lettres sont des variables, car les quantités sont inconnues.
Ou 10 = x
+ y, les formes ou les lettres sont des variables, car les quantités sont inconnues.
Source : En avant, les maths!, 2e année, CM, Algèbre, p. 2.
Connaissance : constante
Les quantités qui restent les mêmes sont appelées constantes.
Exemple
En observant la suite ci-dessous, on remarque qu’à chaque rang/figure, ce qui reste pareil, soit la constante, est le groupe de 8 carrés violets. Ce qui change, ce sont les groupes de carrés rouges.
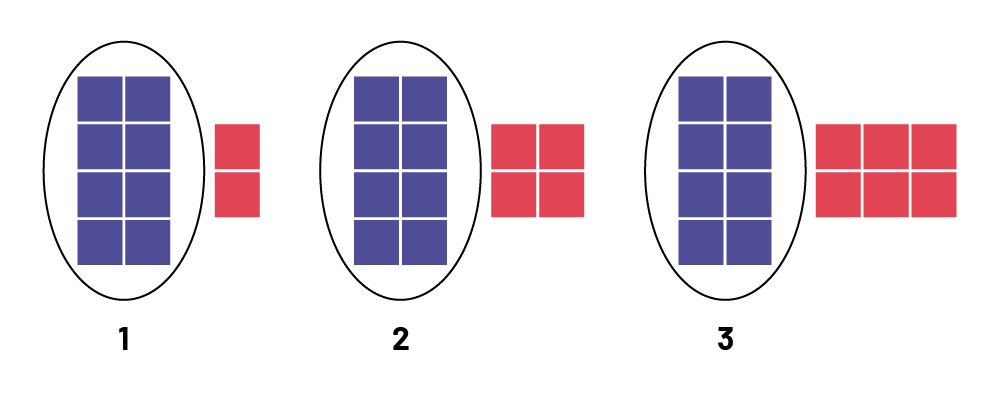 Image Un motif
avec des blocs bleus et rouges. Huit blocs violets, puis 2 blocs rouges. Huit autres blocs bleus et les quatre blocs
rouges. Puis encore huit blocs bleus et 6 blocs rouges. Les blocs constants de huit sont encerclés.
Image Un motif
avec des blocs bleus et rouges. Huit blocs violets, puis 2 blocs rouges. Huit autres blocs bleus et les quatre blocs
rouges. Puis encore huit blocs bleus et 6 blocs rouges. Les blocs constants de huit sont encerclés.
Source : En avant, les maths!, 2e année, CM, Algèbre, p. 2.
