C2.2 Déterminer si des ensembles d’expressions qui comportent des additions, des soustractions, des multiplications et des divisions sont équivalents ou non.
Activité 1 : comparer des expressions avec des dispositions rectangulaires
Une disposition rectangulaire est un ensemble d’objets disposés en rangées et en colonnes de façon à former un rectangle. Les dispositions rectangulaires sont des modèles mathématiques très utiles pour représenter des nombres, des opérations ainsi que leurs propriétés. Elles permettent également d’explorer et de visualiser facilement les relations entre des faits de multiplication.
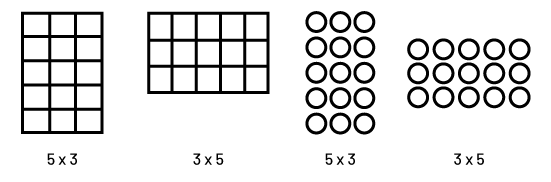 image Motifs géométriques et équations correspondantes. Le premier est une grille verticale de 15 carrés. L'équation ci-dessous est 5 fois 3. Le motif suivant est une grille horizontale de 15 carrés. L'équation ci-dessous est 3 fois 5. Elle est alignée comme la première grille, mais au lieu d'une grille, il s'agit d'une série de cercles. L'équation est la suivante : 5 fois 3. Enfin, 15 cercles en 3 rangées placées horizontalement. L'équation correspondante est 3 fois 5.
image Motifs géométriques et équations correspondantes. Le premier est une grille verticale de 15 carrés. L'équation ci-dessous est 5 fois 3. Le motif suivant est une grille horizontale de 15 carrés. L'équation ci-dessous est 3 fois 5. Elle est alignée comme la première grille, mais au lieu d'une grille, il s'agit d'une série de cercles. L'équation est la suivante : 5 fois 3. Enfin, 15 cercles en 3 rangées placées horizontalement. L'équation correspondante est 3 fois 5.
En algèbre, les dispositions rectangulaires permettent de montrer la propriété de commutativité d’une situation d’égalité.
Introduction aux dispositions rectangulaires
Avant de commencer, préparer du matériel concret et semi-concret qui représente une disposition rectangulaire (par exemple, caisse de boîtes de jus, boîte à œufs, tablette de chocolat, chaises disposées en rangées et en colonnes, illustrations). Présenter le matériel aux élèves et dénombrer avec elles et eux les rangées et les colonnes.
Observer ensuite des illustrations de dispositions rectangulaires (par exemple, illustrations de caisses remplies de boîtes de jus, de tablettes de chocolat regroupées en rangées, d’étalages de fruits ou de légumes). Puis dénombrer les rangées et les colonnes dans ces dispositions. Établir le lien avec un cadre à 10 cases.
Demander aux élèves de concevoir un cadre à 12 cases sur du papier quadrillé. Comparer les différentes dispositions possibles (4 rangées et 3 colonnes; 3 rangées et 4 colonnes; 2 rangées et 6 colonnes; 6 rangées et 2 colonnes; 1 rangée et 12 colonnes; 12 rangées et 1 colonne).
Faire remarquer que la forme est toujours rectangulaire et que le nombre de cases est le même dans chaque rangée (par exemple, 2 cases dans chacune des 6 rangées) et dans chaque colonne (par exemple, 6 cases dans chacune des 2 colonnes). Inviter les élèves à déterminer d’autres nombres avec lesquels des dispositions rectangulaires semblables peuvent être réalisées.
Activité
Former des équipes de deux et leur demander de déterminer sans avoir recours au calcul si ces deux expressions sont équivalentes à l’aide de disposition rectangulaire.
Remettre à chaque équipe des feuilles de papier quadrillé grand format et des ciseaux.

Par exemple, les élèves pourraient découper une disposition rectangulaire comme suit :
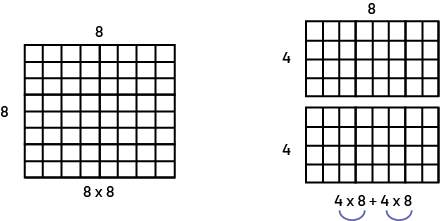 image Une grille de 64 cases. « 8 » verticalement et « 8 » horizontalement. Sous la grille est l'équation 8 fois 8. 2 grilles. 4 verticalement et « 8 » horizontalement. Une équation ci-dessous montre 4 fois « 8 » plus 4 fois 8.
image Une grille de 64 cases. « 8 » verticalement et « 8 » horizontalement. Sous la grille est l'équation 8 fois 8. 2 grilles. 4 verticalement et « 8 » horizontalement. Une équation ci-dessous montre 4 fois « 8 » plus 4 fois 8.
Faire une mise en commun avec les élèves en affichant quelques exemples de disposition rectangulaire afin de montrer que les deux expressions sont équivalentes puisque la quantité des carrés reste la même si on la coupe en deux.
Leur demander de trouver d’autres expressions et de les illustrer pour montrer que la stratégie fonctionne de façon systématique.
Exemple

Sans avoir recours au calcul, les élèves peuvent déjà remarquer que l’expression numérique de gauche est également représentée à droite du symbole de l’égalité, mais en deux parties distinctes. Demander ensuite aux élèves de représenter des phrases mathématiques au moyen de dispositions rectangulaires ouvertes.
Exemple

Leur demander de trouver d’autres expressions qui représentent une équivalence que leurs pairs pourront valider. L’important est de découvrir les relations qui existent de part et d’autre du signe d’égalité. Les élèves sont alors en mesure de formuler une conjecture qu’elles et ils vérifient avec d’autres exemples.
Exemple

Source : Guide d’enseignement efficace des mathématiques de la maternelle à la 3e année, p. 73-76.
Activité 2 : comparer des expressions avec une balance mathématique
Deux modèles de balances sont utilisés pour explorer les concepts algébriques : la balance à plateaux et la balance mathématique. Grâce à ce matériel de manipulation, les élèves du cycle primaire peuvent vérifier en un coup d’œil et confirmer, le cas échéant, des situations d’équivalence entre des quantités. Par le fait même, elles et ils peuvent explorer diverses stratégies pour représenter, maintenir ou rétablir l’égalité entre les quantités.

Introduction à la balance à plateaux
La balance à plateaux peut, dans la mesure où les objets qui y sont placés ont la même masse, favoriser la compréhension du concept d’égalité en algèbre puisque la relation entre les quantités d’objets dans chacun des plateaux est concrète et apparente.
Note : Il faut s’assurer que, lorsque les élèves se servent d’une balance, elles et ils se basent non seulement sur la masse pour établir l’équilibre, mais aussi sur les quantités. Le fait de simplement comparer les quantités contenues sur les plateaux n’est pas suffisant en algèbre. Les élèves doivent explorer les relations qui existent entre ces quantités. Certains auteurs et auteures déconseillent l’usage de la balance à plateaux en algèbre au cycle primaire, car les élèves confondent facilement les concepts de quantité et de masse.
Si vous utilisez la balance à plateaux, assurez-vous d’utiliser des objets ayant tous la même masse (par exemple, des cubes emboîtables).
Introduction à la balance mathématique
Présenter les différentes parties de la balance mathématique en utilisant les termes appropriés (par exemple, le levier, le point d’appui, la languette).
Placer deux languettes à un nombre à gauche du levier (par exemple, au nombre 3). Demander aux élèves de décrire la position du levier.
Poser la question suivante :
- Que faut-il faire pour placer la balance en équilibre?
Échanger avec les élèves pour leur faire réaliser que :
- la partie abaissée du levier représente la quantité la plus élevée;
- dans cette situation, une quantité doit être ajoutée au côté droit du levier pour rétablir l’équilibre;
- la balance est en équilibre si les quantités sont égales sur les deux côtés du levier;
- de chaque côté de la balance, les quantités ajoutées peuvent être représentées par différentes expressions numériques telles que 2 × 3, 5 + 1, 3 × 2, 1 + 1 + 4.
Présenter cette situation aux élèves :
Lucie a placé une languette sur le 8, du côté gauche d’une balance mathématique et une autre languette sur le 4, du côté droit de la balance.

Que doit-elle faire pour créer une situation d’égalité si elle doit effectuer au moins une opération de chaque côté de la balance? Modeler une solution possible. Par exemple, déplacer la languette sur le côté gauche de la balance du 8 vers le 6 (– 2) et ajouter 2.

S’assurer que les élèves constatent que la balance est maintenant en équilibre et qu’elle décrit alors une situation d’égalité.
Pour chaque étape, écrire une phrase mathématique :
8 ≠ 4
8 – 2 = 4 + 2
6 = 6
Demander aux élèves de reprendre la démarche afin de trouver une autre solution.
Source : Guide d’enseignement efficace des mathématiques de la maternelle à la 3e année, p. 78-79.
