C3. Codage
Mettre en application ses habiletés en codage pour résoudre des problèmes et créer des représentations de situations mathématiques de façons computationnelles, à l’aide de concepts et d’habiletés en codage.
Situation d’apprentissage : Les biscuits sans fin
Durée totale : de 140 à 150 minutes
Sommaire
Les élèves pourront mettre en pratique les faits de multiplication ainsi que la disposition rectangulaire en créant un code pour la machine du boulanger.
| Attentes | Contenus d'apprentissage |
|---|---|
| B2. Sens des opérations Utiliser ses connaissances des nombres et des opérations pour résoudre des problèmes mathématiques de la vie quotidienne. |
B2.4 Démontrer sa compréhension des algorithmes de l’addition et de la soustraction de
nombres naturels en établissant des liens avec les outils et les stratégies utilisés pour additionner et
soustraire, et décrire ces liens.
B2.6 Représenter la multiplication de nombres jusqu’à 10 × 10 et la division de nombres jusqu’à 100 ÷ 10 à l’aide d’une variété d’outils et de schémas, y compris des dispositions rectangulaires. |
| C3. Codage Résoudre des problèmes et créer des représentations de situations mathématiques de façon computationnelle à l’aide de concepts et d’habiletés en codage. |
C3.1 Résoudre des problèmes et créer des représentations de situations mathématiques de
façon computationnelle en écrivant et en exécutant des codes, y compris des codes comprenant des événements
séquentiels, simultanés et répétitifs.
C3.2 Lire et modifier des codes donnés, y compris des codes comprenant des événements séquentiels, simultanés et répétitifs, et décrire l’incidence de ces changements sur les résultats. |
| Pratiques pédagogiques à fort impact en mathématiques à privilégier | Description |
|---|---|
| Résultats d’apprentissage, critères d’évaluation et rétroaction descriptive | Afficher, dans la salle de classe, les critères d’évaluation pour que les élèves s’y réfèrent pendant leur travail. Tout le long de l’activité, prendre le temps de circuler dans la salle de classe et d’observer ce que font les élèves. Les interroger au sujet de leur travail et leur donner une rétroaction descriptive liée aux critères d’évaluation affichés. |
| Conversations mathématiques | Dans la mise en situation, les élèves auront l’occasion de discuter des solutions possibles à apporter au code. Au cours de cette discussion, elles et ils pourront écouter les opinions des autres élèves, expliquer leur raisonnement et ajouter des idées à celles des autres. |
| Outils et représentations | Les élèves mettent en pratique leur connaissance des multiplications et solidifient leur apprentissage en les représentant à l’aide de dispositions rectangulaires. Elles et ils pourront modéliser diverses situations de façon visuelle et les comparer avec d’autres représentations. L’utilisation efficace d’outils et de représentations signifie que les différentes représentations sont valorisées et que des liens seront établis entre elles. |
| Connaissances et habiletés préalables |
|---|
|
Résultats d’apprentissage
À la fin de cette situation d’apprentissage, l’élève pourra :
- écrire et exécuter le code d’une représentation de disposition rectangulaire;
- ajouter une ou plusieurs boucles dans son code afin de le rendre plus efficace;
- utiliser les faits numériques de multiplication pour s’aider à disposer des pâtisseries de façon efficace sur une plaque à pâtisserie.
| Compétences | Critère(s) d’évaluation |
|---|---|
| Connaissance et compréhension |
|
| Habiletés de la pensée |
|
| Communication |
|
| Mise en application |
|
Matériel requis
- ordinateur et application ou logiciel de codage au choix
- annexe (Mise en situation)
Note : Les exemples dans cette situation d’apprentissage ont été créés à partir de Scratch.
Vocabulaire mathématique
disposition rectangulaire, code, événements séquentiels, événements simultanés, événements répétitifs, boucle, variable
Mise en situation
Durée : 30 minutes
L’évaluation peut se faire par les…
Présenter aux élèves la photo ci-dessous. Leur demander les questions qu’elles et ils pourraient se poser concernant la photo ou les observations qu’elles et ils pourraient faire au sujet de la photo (je remarque, je me demande).

Exemples de questions ou d’observations :
- Combien de biscuits y a-t-il en tout?
- Comment peux-tu déterminer le nombre de biscuits sans les compter un par un?
- Je vois une plaque à pâtisserie sur laquelle il y a 4 rangées de 5 biscuits et une plaque à pâtisserie sur laquelle il y a 2 rangées de 3 biscuits.
- Je crois qu’il y a 20 biscuits sur la plaque à pâtisserie du bas, même si je ne vois pas la rangée du haut, car 4 × 5 = 20.
| Observations possibles | Pistes d’intervention |
|---|---|
| L’élève ne sait pas par où commencer. | Que dois-tu faire actuellement? Que vois-tu? |
| L’élève n’arrive pas à faire des liens avec ses connaissances antérieures en mathématiques. | Que remarques-tu dans la photo qui te fait penser aux mathématiques? Est-ce que tu sais combien il y a de biscuits? Comment le sais-tu? |
| L’élève a de la difficulté à exprimer, à l’aide du vocabulaire mathématique, ce qu’elle ou il remarque. | Est-ce que le nombre de biscuits pourrait être représenté à l’aide d’une addition répétée? Est-ce que cette addition répétée pourrait être représentée par une multiplication? Sur la plaque à pâtisserie du bas, combien de rangées de biscuits y a-t-il? Combien de biscuits y a-t-il dans chaque rangée? |
Déroulement
Durée : 100 minutes
L’évaluation peut se faire par les…
Présenter aux élèves la situation ci-dessous ainsi que le code :
À la boulangerie, Maxime doit planifier où mettre les pâtisseries sur les plaques à pâtisserie avant de les faire cuire. La machine qui place les pâtisseries sur une plaque à pâtisserie utilise un logiciel de codage en blocs. Maxime crée le code ci-dessous afin de mettre 24 pâtisseries sur une plaque.
Exemple du code de Maxime :
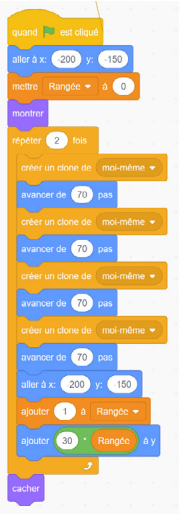 image Un
bloc de codage commençant par un bloc de contrôle qui montre « quand » un drapeau vert « est cliqué ». Ce bloc est
empilé sur un bloc de mouvement qui montre « aller à x » et une bulle montrant « moins 200 », « i grec » et une bulle
montrant « moins 150 ». Empilé sur le bloc de variables suivant qui montre le mot « mettre » puis « Rangé » avec une
flèche vers le bas, à côté de cela « à » « Zéro » dans une bulle. Ce bloc est empilé sur un bloc d'apparence avec le
mot « montrer ». Ce bloc est empilé sur un nouveau bloc de contrôle qui commence par un bloc indiquant « répéter », «
6 » dans un cercle suivi du mot « fois ». En dessous est empilé un autre bloc de contrôle qui montre « créer un clone
de » dans une autre bulle « moi-même » avec une flèche vers le bas. Le bloc suivant dans la pile est un bloc de
mouvement qui montre « avancer de » une bulle montre « 70 », « pas ». La séquence de contrôle se répète trois fois,
puis elle est empilée sur un bloc de mouvement qui montre « aller à x » et une bulle montrant « moins 200 », « i grec
» et une bulle montrant « moins 150 ». En dessous, un bloc de variables indique « ajouter » et une bulle indiquant «
un » « à », puis « Rangé » avec une flèche vers le bas, à côté de « à » « i grec ». En dessous, un bloc de variables
indique « ajouter » et une bulle indiquant « 30 », puis « Rangé » avec une flèche vers le bas, à côté de « à » « i
grec ». La séquence se termine par un bloc d'apparence avec le mot « cacher ».
image Un
bloc de codage commençant par un bloc de contrôle qui montre « quand » un drapeau vert « est cliqué ». Ce bloc est
empilé sur un bloc de mouvement qui montre « aller à x » et une bulle montrant « moins 200 », « i grec » et une bulle
montrant « moins 150 ». Empilé sur le bloc de variables suivant qui montre le mot « mettre » puis « Rangé » avec une
flèche vers le bas, à côté de cela « à » « Zéro » dans une bulle. Ce bloc est empilé sur un bloc d'apparence avec le
mot « montrer ». Ce bloc est empilé sur un nouveau bloc de contrôle qui commence par un bloc indiquant « répéter », «
6 » dans un cercle suivi du mot « fois ». En dessous est empilé un autre bloc de contrôle qui montre « créer un clone
de » dans une autre bulle « moi-même » avec une flèche vers le bas. Le bloc suivant dans la pile est un bloc de
mouvement qui montre « avancer de » une bulle montre « 70 », « pas ». La séquence de contrôle se répète trois fois,
puis elle est empilée sur un bloc de mouvement qui montre « aller à x » et une bulle montrant « moins 200 », « i grec
» et une bulle montrant « moins 150 ». En dessous, un bloc de variables indique « ajouter » et une bulle indiquant «
un » « à », puis « Rangé » avec une flèche vers le bas, à côté de « à » « i grec ». En dessous, un bloc de variables
indique « ajouter » et une bulle indiquant « 30 », puis « Rangé » avec une flèche vers le bas, à côté de « à » « i
grec ». La séquence se termine par un bloc d'apparence avec le mot « cacher ».
Questions à poser aux élèves :
- Que remarques-tu?
- Que cherche-t-on à faire avec ce code? (Mettre 24 pâtisseries sur une plaque à pâtisserie.)
- Combien de pâtisseries penses-tu qu’il y aura sur la plaque à pâtisserie? (Il y aura 8 pâtisseries sur la plaque à pâtisserie.)
- Quel bloc de code « met » une pâtisserie sur la plaque à pâtisserie? Combien de fois est-il présent dans le code?
Le bloc « créer un clône de moi-même » met la pâtisserie sur la plaque à pâtisserie. Ce bloc est présent 4 fois, mais dans une boucle de 2 répétitions, donc \(2 \times 4 = 8 \).
- Quelles questions te poses-tu?
- Pourrais-tu me dire, dans tes propres mots, ce que dit ce code?
Inviter les élèves à créer un pseudocode qui représente le code de Maxime afin de pouvoir prédire ce qui arrivera lorsque le code sera exécuté. Puis, leur demander si le code de Maxime produira le résultat souhaité.
Exemples de réflexions :
- Je remarque une boucle, ce qui veut dire qu’une série de blocs est répétée.
- Je remarque que des blocs de variable sont utilisés. Je ne me suis jamais servi de variables.
- Je pense que 8 objets seront créés parce que la boucle se répète 2 fois. Dans la boucle, il y a l’événement « faire un clône » qui se répète 4 fois, \(2 \times 4 = 8 \).
- Je me demande comment je vais créer une variable.
Exemple de pseudocode possible :
|
Aller à la position de départ. |
|
Mettre la variable « rangée » à zéro. |
|
Montrer l’objet. |
|
Répéter 2 fois. |
|
Avancer de 70 pas Faire une copie du sprite. |
|
Avancer de 70 pas Faire une copie du sprite. |
|
Avancer de 70 pas Faire une copie du sprite. |
|
Avancer de 70 pas Faire une copie du sprite. |
|
Retourner à la position de départ. |
|
Ajouter 1 à la variable de la rangée, donc monter de 1. |
|
Ajouter 30 × (valeur de « rangée »), donc 30 × 1*. |
|
Cacher l’objet. |
* Cette partie du code déplace le sprite au début de la bonne rangée. Dans ce cas-ci, chaque rangée est espacée de 30 pixels. Donc, la première rangée (rangée = 0) commence à la position de départ, la deuxième rangée (rangée = 1) commence à la position de départ + 30, la troisième rangée (rangée = 2) commence à la position de départ + 60, etc.
Note : Certaines et certains élèves remarqueront peut-être que la partie « Avancer de 70 pas, faire une copie du sprite » se répète 4 fois, et demanderont si ce serait possible d’utiliser une boucle pour simplifier le code. C’est en fait possible. Ce genre de structure est élaboré davantage en 4e année (événements imbriqués). Cela étant dit, voici à quoi pourrait ressembler le code comportant cette structure, au cas où ce serait une des pistes de questionnement des élèves.
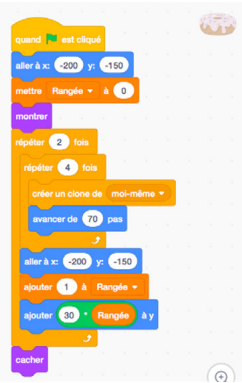 image Un
bloc de codage commençant par un bloc de contrôle qui montre « quand » un drapeau vert « est cliqué ». Ce bloc est
empilé sur un bloc de mouvement qui montre « aller à « x » » et une bulle montrant « moins 200 », « i grec » et une
bulle montrant « moins 150 ». Empilé sur le bloc variable suivant qui montre le mot « mettre » puis « Rangé » avec une
flèche vers le bas, à côté de cela « à » « Zéro » dans une bulle. Ce bloc est empilé sur un bloc d'apparence avec le
mot « montrer ». Ce bloc est empilé sur un nouveau bloc de contrôle qui commence par un bloc indiquant « répéter », «
2 » dans un cercle suivi du mot « fois ». Ce bloc est empilé sur un nouveau bloc de contrôle qui commence par un bloc
qui montre « répéter », « 4 » dans un cercle suivi du mot « fois ». En dessous est empilé un autre bloc de contrôle
qui montre « créer un clone de » dans une autre bulle « moi-même » avec une flèche vers le bas. Le bloc suivant dans
la pile est un bloc de mouvement qui affiche « avancer de » dans une bulle affichant « 70 », « pas ». Ce bloc est
empilé sur un bloc de mouvement qui montre « aller à x » : et une bulle montrant « moins 200 », « i grec » : et une
bulle montrant « moins 150 ». En dessous se trouve un bloc de variables indiquant « ajouter » et une bulle indiquant «
un » « à » puis « Rangé » avec une flèche vers le bas, à côté de « à » « i grec ». La séquence se termine par un bloc
d'apparence avec le mot « cacher ».
image Un
bloc de codage commençant par un bloc de contrôle qui montre « quand » un drapeau vert « est cliqué ». Ce bloc est
empilé sur un bloc de mouvement qui montre « aller à « x » » et une bulle montrant « moins 200 », « i grec » et une
bulle montrant « moins 150 ». Empilé sur le bloc variable suivant qui montre le mot « mettre » puis « Rangé » avec une
flèche vers le bas, à côté de cela « à » « Zéro » dans une bulle. Ce bloc est empilé sur un bloc d'apparence avec le
mot « montrer ». Ce bloc est empilé sur un nouveau bloc de contrôle qui commence par un bloc indiquant « répéter », «
2 » dans un cercle suivi du mot « fois ». Ce bloc est empilé sur un nouveau bloc de contrôle qui commence par un bloc
qui montre « répéter », « 4 » dans un cercle suivi du mot « fois ». En dessous est empilé un autre bloc de contrôle
qui montre « créer un clone de » dans une autre bulle « moi-même » avec une flèche vers le bas. Le bloc suivant dans
la pile est un bloc de mouvement qui affiche « avancer de » dans une bulle affichant « 70 », « pas ». Ce bloc est
empilé sur un bloc de mouvement qui montre « aller à x » : et une bulle montrant « moins 200 », « i grec » : et une
bulle montrant « moins 150 ». En dessous se trouve un bloc de variables indiquant « ajouter » et une bulle indiquant «
un » « à » puis « Rangé » avec une flèche vers le bas, à côté de « à » « i grec ». La séquence se termine par un bloc
d'apparence avec le mot « cacher ».
- Demander aux élèves de recréer le code en utilisant le logiciel choisi.
- Inviter les élèves à modifier le code de Maxime pour qu’il comprenne 24 pâtisseries, comme souhaité au départ.
Note : Cela sera une bonne occasion d’essayer différentes fonctions et de modeler l’approche essai et erreur en appliquant le processus d’élimination ou le processus d’essais systématiques. Encourager les élèves à sauvegarder le code aussitôt qu’il est fonctionnel et à en faire une copie à partir de laquelle elles et ils essayeront différentes fonctions ou verront l’effet de la modification d’un bloc. De cette façon, l’élève pourra toujours retourner à son code fonctionnel (le risque associé aux erreurs est donc très faible, ce qui encouragera l’expérimentation).
Réponse possible
Ce code met 8 biscuits sur la plaque à pâtisserie (2 répétitions de 4 biscuits). Je sais que chaque répétition de plus ajoutera 4 pâtisseries sur la plaque à pâtisserie. Je peux donc faire une addition répétée de 4 jusqu’à ce que j’atteigne 24 pâtisseries.
Alors, 4 + 4 + 4 + 4 + 4 + 4 = 24, j’ai donc besoin de modifier la boucle de manière à avoir 6 répétitions (6 × 4 = 24).
Exemple de code :
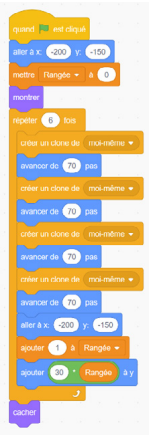 image Un
bloc de codage commençant par un bloc de contrôle qui montre « quand » un drapeau vert « est cliqué ». Ce bloc est
empilé sur un bloc de mouvement qui montre « aller à « x » » et une bulle montrant « moins 200 », « i grec » et une
bulle montrant « moins 150 ». Empilé sur le bloc variable suivant qui montre le mot « mettre » puis « Rangé » avec une
flèche vers le bas, à côté de cela « à » « Zéro » dans une bulle. Ce bloc est empilé sur un bloc d'apparence avec le
mot « montrer ». Ce bloc est empilé sur un nouveau bloc de contrôle qui commence par un bloc indiquant « répéter »,
«12 » dans un cercle suivi du mot « fois ». En dessous est empilé un autre bloc de contrôle qui montre « créer un
clone de » dans une autre bulle « moi-même » avec une flèche vers le bas. Le bloc suivant dans la pile est un bloc de
mouvement qui affiche « avancer de » dans une bulle affichant « 70 », « pas ». Ce bloc est empilé sur un bloc de
mouvement qui montre « aller à x » : et une bulle montrant « moins 200 », « i grec » : et une bulle montrant « moins
150 ». En dessous se trouve un bloc de variables indiquant « ajouter » et une bulle indiquant « un » « à » puis «
Rangé » avec une flèche vers le bas, à côté de « à » « i grec ». La séquence se termine par un bloc d'apparence avec
le mot « cacher ».
image Un
bloc de codage commençant par un bloc de contrôle qui montre « quand » un drapeau vert « est cliqué ». Ce bloc est
empilé sur un bloc de mouvement qui montre « aller à « x » » et une bulle montrant « moins 200 », « i grec » et une
bulle montrant « moins 150 ». Empilé sur le bloc variable suivant qui montre le mot « mettre » puis « Rangé » avec une
flèche vers le bas, à côté de cela « à » « Zéro » dans une bulle. Ce bloc est empilé sur un bloc d'apparence avec le
mot « montrer ». Ce bloc est empilé sur un nouveau bloc de contrôle qui commence par un bloc indiquant « répéter »,
«12 » dans un cercle suivi du mot « fois ». En dessous est empilé un autre bloc de contrôle qui montre « créer un
clone de » dans une autre bulle « moi-même » avec une flèche vers le bas. Le bloc suivant dans la pile est un bloc de
mouvement qui affiche « avancer de » dans une bulle affichant « 70 », « pas ». Ce bloc est empilé sur un bloc de
mouvement qui montre « aller à x » : et une bulle montrant « moins 200 », « i grec » : et une bulle montrant « moins
150 ». En dessous se trouve un bloc de variables indiquant « ajouter » et une bulle indiquant « un » « à » puis «
Rangé » avec une flèche vers le bas, à côté de « à » « i grec ». La séquence se termine par un bloc d'apparence avec
le mot « cacher ».
Demander aux élèves de circuler dans la salle de classe afin de voir les codes des autres élèves. Est-ce que toutes et tous les élèves ont choisi de faire la même modification? Est-ce que le résultat demeure le même?
Exemples de codes possibles (toujours pour 24 biscuits) :
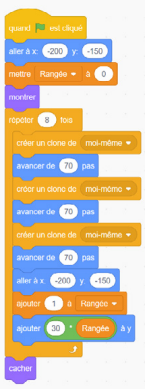 image Un bloc de codage commençant par un bloc de contrôle qui montre «
quand » un drapeau vert « est cliqué ». Ce bloc est empilé sur un bloc de mouvement qui montre « aller à x » et
une bulle montrant « moins 200 », « i grec » et une bulle montrant « moins 150 ». Empilé sur le bloc de variables
suivant qui montre le mot « mettre » puis « Rangé » avec une flèche vers le bas, à côté de cela « à » « Zéro »
dans une bulle. Ce bloc est empilé sur un bloc d'apparence avec le mot « montrer ». Ce bloc est empilé sur un
nouveau bloc de contrôle qui commence par un bloc indiquant « répéter », « 6 » dans un cercle suivi du mot « fois
». En dessous est empilé un autre bloc de contrôle qui montre « créer un clone de » dans une autre bulle «
moi-même » avec une flèche vers le bas. Le bloc suivant dans la pile est un bloc de mouvement qui montre « avancer
de » une bulle montre « 70 », « pas ». La séquence de contrôle se répète trois fois, puis elle est empilée sur un
bloc de mouvement qui montre « aller à x » et une bulle montrant « moins 200 », « i grec » et une bulle montrant «
moins 150 ». En dessous, un bloc de variables indique « ajouter » et une bulle indiquant « un » « à », puis «
Rangé » avec une flèche vers le bas, à côté de « à » « i grec ». En dessous, un bloc de variables indique «
ajouter » et une bulle indiquant « 30 », puis « Rangé » avec une flèche vers le bas, à côté de « à » « i grec ».
La séquence se termine par un bloc d'apparence avec le mot « cacher ».
image Un bloc de codage commençant par un bloc de contrôle qui montre «
quand » un drapeau vert « est cliqué ». Ce bloc est empilé sur un bloc de mouvement qui montre « aller à x » et
une bulle montrant « moins 200 », « i grec » et une bulle montrant « moins 150 ». Empilé sur le bloc de variables
suivant qui montre le mot « mettre » puis « Rangé » avec une flèche vers le bas, à côté de cela « à » « Zéro »
dans une bulle. Ce bloc est empilé sur un bloc d'apparence avec le mot « montrer ». Ce bloc est empilé sur un
nouveau bloc de contrôle qui commence par un bloc indiquant « répéter », « 6 » dans un cercle suivi du mot « fois
». En dessous est empilé un autre bloc de contrôle qui montre « créer un clone de » dans une autre bulle «
moi-même » avec une flèche vers le bas. Le bloc suivant dans la pile est un bloc de mouvement qui montre « avancer
de » une bulle montre « 70 », « pas ». La séquence de contrôle se répète trois fois, puis elle est empilée sur un
bloc de mouvement qui montre « aller à x » et une bulle montrant « moins 200 », « i grec » et une bulle montrant «
moins 150 ». En dessous, un bloc de variables indique « ajouter » et une bulle indiquant « un » « à », puis «
Rangé » avec une flèche vers le bas, à côté de « à » « i grec ». En dessous, un bloc de variables indique «
ajouter » et une bulle indiquant « 30 », puis « Rangé » avec une flèche vers le bas, à côté de « à » « i grec ».
La séquence se termine par un bloc d'apparence avec le mot « cacher ».
Représente 12 × 2 = 24
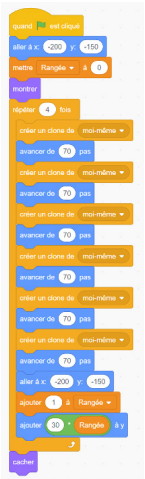 image Un bloc de codage commençant par un bloc de contrôle qui montre «
quand » un drapeau vert « est cliqué ». Ce bloc est empilé sur un bloc de mouvement qui montre « aller à x » et
une bulle montrant « moins 200 », « i grec » et une bulle montrant « moins 150 ». Empilé sur le bloc de variables
suivant qui montre le mot « mettre » puis « Rangé » avec une flèche vers le bas, à côté de cela « à » « Zéro »
dans une bulle. Ce bloc est empilé sur un bloc d'apparence avec le mot « montrer ». Ce bloc est empilé sur un
nouveau bloc de contrôle qui commence par un bloc indiquant « répéter », « 6 » dans un cercle suivi du mot « fois
». En dessous est empilé un autre bloc de contrôle qui montre « créer un clone de » dans une autre bulle «
moi-même » avec une flèche vers le bas. Le bloc suivant dans la pile est un bloc de mouvement qui montre « avancer
de » une bulle montre « 70 », « pas ». La séquence de contrôle se répète cinq fois, puis elle est empilée sur un
bloc de mouvement qui montre « aller à x » et une bulle montrant « moins 200 », « i grec » et une bulle montrant «
moins 150 ». En dessous, un bloc de variables indique « ajouter » et une bulle indiquant « un » « à », puis «
Rangé » avec une flèche vers le bas, à côté de « à » « i grec ». En dessous, un bloc de variables indique «
ajouter » et une bulle indiquant « 30 », puis « Rangé » avec une flèche vers le bas, à côté de « à » « i grec ».
La séquence se termine par un bloc d'apparence avec le mot « cacher ».
image Un bloc de codage commençant par un bloc de contrôle qui montre «
quand » un drapeau vert « est cliqué ». Ce bloc est empilé sur un bloc de mouvement qui montre « aller à x » et
une bulle montrant « moins 200 », « i grec » et une bulle montrant « moins 150 ». Empilé sur le bloc de variables
suivant qui montre le mot « mettre » puis « Rangé » avec une flèche vers le bas, à côté de cela « à » « Zéro »
dans une bulle. Ce bloc est empilé sur un bloc d'apparence avec le mot « montrer ». Ce bloc est empilé sur un
nouveau bloc de contrôle qui commence par un bloc indiquant « répéter », « 6 » dans un cercle suivi du mot « fois
». En dessous est empilé un autre bloc de contrôle qui montre « créer un clone de » dans une autre bulle «
moi-même » avec une flèche vers le bas. Le bloc suivant dans la pile est un bloc de mouvement qui montre « avancer
de » une bulle montre « 70 », « pas ». La séquence de contrôle se répète cinq fois, puis elle est empilée sur un
bloc de mouvement qui montre « aller à x » et une bulle montrant « moins 200 », « i grec » et une bulle montrant «
moins 150 ». En dessous, un bloc de variables indique « ajouter » et une bulle indiquant « un » « à », puis «
Rangé » avec une flèche vers le bas, à côté de « à » « i grec ». En dessous, un bloc de variables indique «
ajouter » et une bulle indiquant « 30 », puis « Rangé » avec une flèche vers le bas, à côté de « à » « i grec ».
La séquence se termine par un bloc d'apparence avec le mot « cacher ».
Représente 4 × 6 = 24
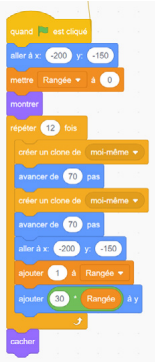
Représente 8 × 3 = 24
Exemples de réflexions :
- Non, les codes des autres élèves sont différents. J’ai choisi de faire 6 rangées de 4 pâtisseries, mais j’ai vu aussi 8 rangées de 3 pâtisseries et 4 rangées de 6 pâtisseries.
- Il y a plusieurs multiplications qui font 24, mais je pense que 4 rangées de 6 pâtisseries est la meilleure multiplication pour bien utiliser l’espace.
- Les résultats sont pareils, il y a toujours 24 pâtisseries sur la plaque à pâtisserie.
- Les résultats sont différents, même s’il y a toujours 24 pâtisseries sur la plaque à pâtisserie, car la disposition des pâtisseries est différente.
Demander aux élèves de créer un code pour les commandes d’aujourd’hui.
- 20 scones aux canneberges
- 81 biscuits aux raisins
- 47 chaussons aux framboises
Poser des questions aux élèves pour savoir si elles et ils ont les mêmes représentations que les autres élèves.
Réponses possibles
20 scones aux canneberges :
- J’ai utilisé la multiplication 2 × 10 et Valérie a utilisé la multiplication 4 × 5.
- Je crois que la disposition rectangulaire de 2 × 10 n’est pas aussi efficace que celle de 4 × 5, puisqu’on gaspille beaucoup d’espace sur la plaque à pâtisserie.
- Je remarque qu’il y a plusieurs façons de représenter 20 biscuits en utilisant la disposition rectangulaire: 4 × 5, 5 × 4, 2 × 10 et 10 × 2.
81 biscuits aux raisins :
- Il y a juste une façon de représenter ce nombre, puisqu’il y a juste une multiplication qui a un produit de 81, soit 9 × 9.
Note : Les faits de multiplication jusqu’à 10 × 10 sont priorisés dans cette situation d’apprentissage. Toutefois, il est possible d’accepter les réponses 3 × 27 ou 27 × 3 si celles-ci sont proposées.
- Je remarque que les pâtisseries forment un carré.
47 chaussons aux framboises :
Il n’y a pas deux nombres qui, multipliés, donnent 47, mais je sais que 9 × 5 = 45. Je peux d’abord créer un code pour mettre 45 chaussons sur la plaque à pâtisserie (9 rangées de 5 chaussons) et ensuite en ajouter deux autres sur le côté.
Exemple de code :
image Blocs de codage attachés les uns avec les autres.Bloc de départ : drapeau vert.Bloc de mouvement : aller à « x » moins 200, « y » moins 150.Bloc de variable : mettre rangée à zéro.Bloc apparence : montrer.Bloc de contrôle : répéter 9 fois.Bloc de mouvement : avancer de 70 pas.Bloc de contrôle : créer un clone de moi-même.Bloc de mouvement : avancer de 70 pas.Bloc de mouvement : aller à « x » moins 200, « y » moins 150.Bloc de variable : ajouter un à rangée.Bloc de mouvement : ajouter 30 rangées à « y ».Bloc de mouvement : avancer de 70 pas.Bloc de contrôle : créer un clone de moi-même.Bloc de mouvement : avancer de 70 pas.Bloc de contrôle : créer un clone de moi-même.Bloc apparence : cacher.2 papillons adhésifs ajoutent des commentaires :Le premier : La boucle et son contenu créent une disposition rectangulaire de 9 rangées de 5 chaussons ou 9 multiplié par 5 égal 45.Le deuxième : les blocs à l’extérieur de la boucle créent les deux objets supplémentaires afin d’obtenir 47.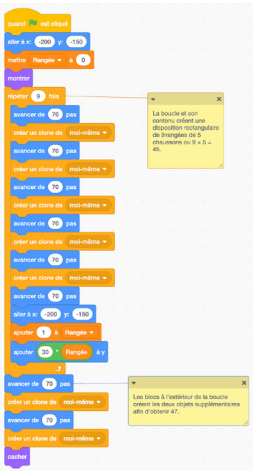
Note : Ce même raisonnement pourrait être utilisé avec d’autres faits numériques, comme 6 × 7 = 42, et 5 autres font 47.
| Observations possibles | Pistes d’intervention |
|---|---|
| L’élève ne réussit pas à utiliser correctement la boucle. |
|
| L’élève ne modifie pas les déplacements, alors les pâtisseries ne vont pas toutes sur la plaque à pâtisserie ou ne la remplissent pas. |
|
| L’élève oublie de cacher l’objet à la fin du code. Exemple :  |
Note : Il existe plusieurs solutions à ce problème; par exemple, l’élève pourrait ajouter un bloc à la fin du code, qui renvoie le sprite à son endroit d’origine, ce qui crée le même résultat visuel que « cacher » le sprite. |
| L’élève oublie le bloc «créer un clône de moi-même». |
Note : Il existe aussi un bloc nommé «estampiller» qui peut produire un effet semblable. |
Objectivation
Durée : 15 minutes
L’évaluation peut se faire par les observations ou les observations.

Choisir quelques élèves du groupe-classe et leur demander de présenter ou d’expliquer leur code (en utilisant un pseudocode). Pendant cette discussion, demander aux autres élèves du groupe-classe de faire ressortir des ressemblances et des différences entre les codes.
Faire un retour sur l’utilisation efficace de boucles dans un code.
Consolidation
Proposer aux élèves de créer des codes afin de représenter des formes géométriques régulières. Si le logiciel de codage utilisé a une option pour tracer des lignes (par exemple, le « stylo » dans Scratch), les élèves peuvent tracer des formes en utilisant des déplacements et des rotations de sprite. Les boucles permettront de réduire la quantité de code pour atteindre un but.
Pour coder une trajectoire carrée, par exemple, il faut connaître les propriétés du carré (4 angles droits et 4 côtés congrus). Le code pour la trajectoire pourrait donc ressembler à ceci :
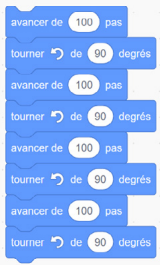
L’ajout de boucles peut réduire le code à ceci :
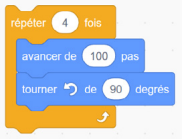
Les élèves peuvent appliquer ce même processus afin de créer un code pour des rectangles.
Liens avec les autres domaines mathématiques (événements répétitifs)
Nombres
B2.6 Représenter la multiplication de nombres jusqu’à 10 × 10 et la division de nombres jusqu’à 100 ÷ 10 à l’aide d’une variété d’outils et de schémas, y compris des dispositions rectangulaires.
En utilisant une boucle, l’élève peut faire le lien entre l’addition répétée et la multiplication. En codant des déplacements et des reproductions de sprites, l’élève peut cheminer d’une représentation de groupes d’objets vers la disposition rectangulaire.
Algèbre
C1.1 Reconnaître et décrire les éléments et les opérations qui se répètent dans diverses suites (numériques et non numériques), y compris des suites trouvées dans la vie quotidienne.
Les séquences de code qui se trouvent à l’intérieur d’une boucle représentent le motif d’une suite à motif répétée. Les élèves peuvent donc utiliser du pseudocode pour décrire l’action à l’intérieur de la boucle.
Sens de l’espace
E2.8 Utiliser des unités de mesure non conventionnelles appropriées pour mesurer l’aire et expliquer l’incidence du chevauchement et des espaces entre les unités sur l’exactitude de la mesure.
En utilisant des événements répétitifs pour faire en sorte qu’une multiplication est représentée en disposition rectangulaire, l’élève peut faire le lien entre le nombre d’objets disposés en rectangle et l’aire.
Différenciation pédagogique et conception universelle de l’apprentissage
- Donner les blocs débranchés aux élèves pour qu’elles et ils les replacent de manière à reproduire le code.
- Donner un pseudocode aux élèves pour qu’elles et ils puissent s’en servir comme plan.
- Proposer aux élèves un code de base pour qu’elles et ils puissent tout simplement aller le modifier selon le nombre de pâtisseries souhaitées.
- Ce code se prête aussi bien aux événements imbriqués, une structure un peu plus complexe, mais qui peut rendre le code plus facile à interpréter. Certaines et certains élèves qui sont plus à l’aise avec le code pourront utiliser cette structure en mettant des boucles à l’intérieur de boucles.
- Pour l’élève qui a besoin d’un défi, il serait possible d’ajouter certains paramètres, par exemple, un maximum de pâtisseries pouvant aller sur une plaque à pâtisserie, ce qui crée une situation mathématique plus complexe à représenter à l’aide du code.
Source : Guide d’enseignement efficace des mathématiques, Codage, p. 73-86.
