C2.3 Résoudre des inégalités qui comprennent des additions et des soustractions de nombres naturels jusqu’à 20, et vérifier et présenter les solutions à l’aide de modèles et de représentations graphiques.
Activité 1 : Résolution d’inégalités
Présenter aux élèves la situation suivante :
Il y a huit chevaux, deux moutons et des vaches dans le pâturage. Le nombre de vaches et de moutons ensemble est plus petit que le nombre de chevaux. Combien de vaches peut-il y avoir dans le pâturage?
Stratégie 1
Résoudre une inégalité à l’aide d’une représentation visuelle
Je représente la situation à l’aide de l’inégalité 2 + v < 8.
J’utilise une représentation visuelle pour la résoudre.
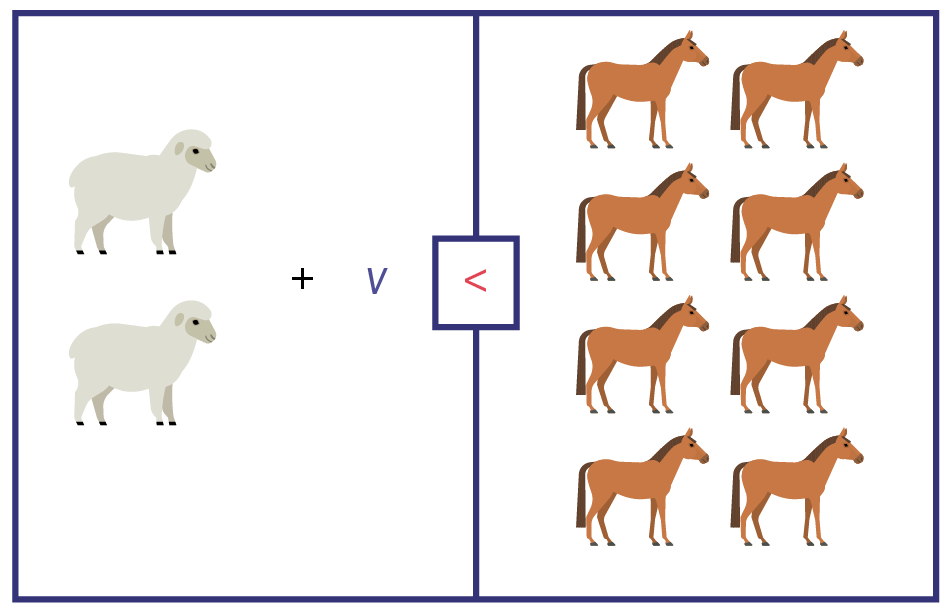
Je sais que le nombre de moutons et de vaches ensemble doit être plus petit que huit. Pour trouver le nombre de vaches, j’utilise le modèle de la balance. Pour maintenir l’équilibre des deux côtés de l’inégalité, je dois appliquer à l’autre côté ce que je fais à un côté. J’enlève alors les deux moutons du côté gauche. Puisque j’enlève deux moutons du côté gauche, j’enlève aussi deux chevaux du côté droit.
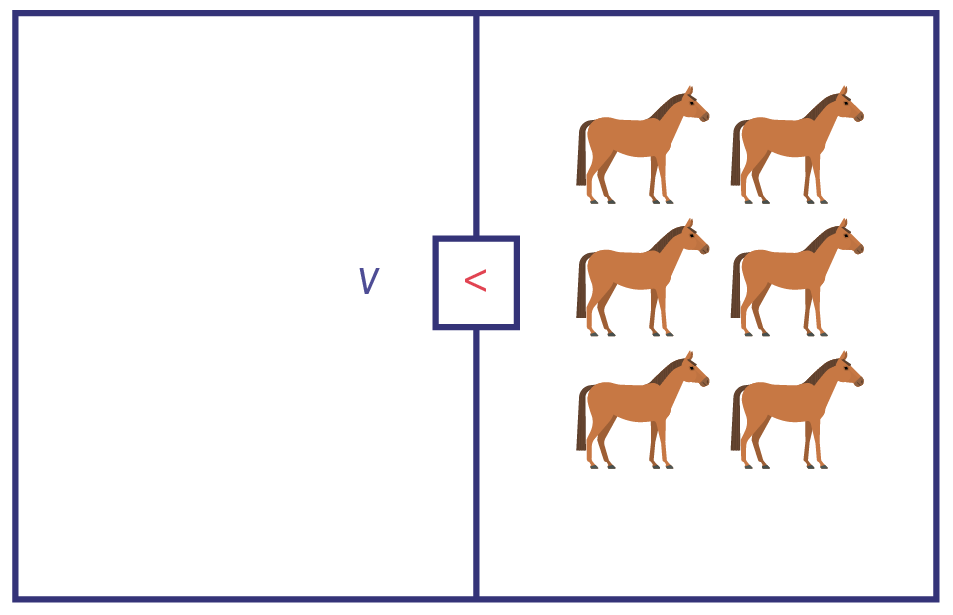
Il reste six chevaux, alors v < 6.
Je vérifie ma réponse :
|
2 + 5 < 8 → 7 < 8 2 + 4 < 8 → 6 < 8 2 + 3 < 8 → 5 < 8 2 + 2 < 8 → 4 < 8 2 + 1 < 8 → 3 < 8 |
Dans le pâturage, il faut qu’il y ait moins de six vaches. Il peut donc y avoir de une à cinq vaches dans le pâturage, puisque, dans le problème, il est mentionné qu’il y a des vaches. Je n’écris donc pas zéro vache.
Stratégie 2
Résoudre une inégalité à l’aide du modèle de la balance
Je résous l’inégalité 2 + v < 8 à l’aide du modèle de la balance.
Je dois isoler la variable v, c’est-à-dire que je dois annuler des valeurs des deux côtés de l’inégalité jusqu’à ce que v soit seul. Pour neutraliser le 2 qui est additionné au v, je dois soustraire 2 de cette même valeur. Pour maintenir la balance des deux côtés, je dois faire la même chose au 8.
La valeur de v est plus petite que 6.
|
2 – 2 + v < 8 – 2 v < 6 |
Pour représenter la solution sur la droite numérique, j’ai placé un point vide sur 6. Cela indique une relation d’inégalité stricte, ce qui veut dire que le nombre de vaches est inférieur à 6. J’ai placé des points sur la droite numérique, puisque les vaches sont entières. Il n’y a pas une fraction de vache dans le pâturage. J’ai mis des points sur les nombres 1 à 5, puisque, dans le problème, il est mentionné qu’il y a des vaches. Je n’écris pas zéro vache.
v < 6

Je vérifie ma réponse :
|
2 + 5 < 8 → 7 < 8 2 + 4 < 8 → 6 < 8 2 + 3 < 8 → 5 < 8 2 + 2 < 8 → 4 < 8 2 + 1 < 8 → 3 < 8 |
Dans le pâturage, il faut qu’il y ait moins de six vaches. Il peut donc y avoir de une à cinq vaches dans le pâturage, puisque, dans le problème, il est mentionné qu’il y a des vaches. Je n’écris donc pas zéro vache.
Source : En avant, les maths!, 4e année, CM, Algèbre, p. 3-5.
Activité 2 : Résoudre une relation d’inégalité stricte
Présenter aux élèves le problème suivant :
Des élèves lisent dans le coin de lecture de la salle de classe. Quatre autres élèves se joignent au groupe. Il y a maintenant moins de 10 personnes dans le coin de lecture. Combien d’élèves lisaient alors dans le coin de lecture au début?
Permettre aux élèves de travailler en équipes pour résoudre le problème.
Exemple
Nous représentons le problème sous la forme d’une inéquation.
Le nombre d’élèves qui lisent dans le coin de lecture est représenté par la variable p.
Quatre personnes de plus se joignent au groupe initial, alors p + 4.
Moins de 10 personnes lisent dans le coin de lecture de la salle de classe, alors p + 4 < 10.
Pour trouver le nombre d’élèves qui lisaient dans le coin de lecture au début, l’inéquation est :
p + 4 < 10
| p | p + 4 | < 10 |
|---|---|---|
| 0 | 4 | oui |
| 1 | 5 | oui |
| 2 | 6 | oui |
| 3 | 7 | oui |
| 4 | 8 | oui |
| 5 | 9 | oui |
| 6 | 10 | non |
| 7 | 11 | non |
Il y avait des élèves qui lisaient dans le coin de lecture de la salle de classe avant que les quatre autres élèves s’ajoutent. Alors, il est impossible qu’il y ait zéro personne ou une personne, donc p = {2, 3, 4, 5}.

Au début, il y avait deux, trois, quatre ou cinq élèves qui lisaient dans le coin de lecture.
Demander à quelques équipes de présenter leur solution. Permettre aux élèves de réviser leur réponse.
Activité 3 : Résoudre une relation d’inégalité large
Présenter aux élèves la mise en situation suivante :
Le petit café du coin peut accueillir jusqu’à 20 personnes dans son établissement. Il y a 11 personnes qui sont assises aux tables. Combien de personnes le petit café peut-il encore accueillir?
Demander aux élèves de résoudre l’inégalité.
Exemple
Nous savons que le nombre de personnes que le petit café du coin peut accueillir est de 20 ou moins, et qu’il y a déjà 11 personnes assises aux tables.
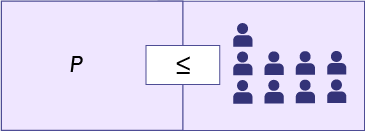
- Nous résolvons l’inéquation 11 + p ≤ 20 à l’aide du modèle de la balance. Pour maintenir l’équilibre des deux côtés de l’inégalité, il faut appliquer à l’autre côté ce que nous avons fait à un côté. Si nous enlevons neuf personnes dans l’encadré de gauche, nous devons également enlever le même nombre de personnes dans l’encadré de droite.
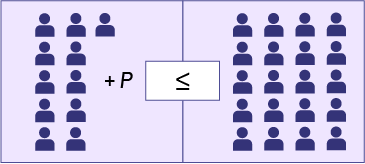
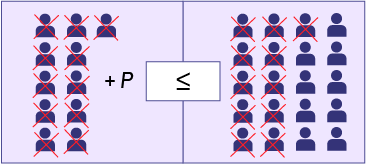
- Nous représentons la solution, sur la droite numérique, en mettant un point plein sur 9, puisqu’il s’agit d’une relation d’inégalité large. Ainsi, le nombre de personnes que le petit café peut encore accueillir est inférieur ou égal à 9.

Nous vérifions la réponse :
|
11 + 9 ≤ 20 → 20 ≤ 20 11 + 8 ≤ 20 → 19 ≤ 20 11 + 7 ≤ 20 → 18 ≤ 20 11 + 6 ≤ 20 → 17 ≤ 20 11 + 5 ≤ 20 → 16 ≤ 20 11 + 4 ≤ 20 → 15 ≤ 20 11 + 3 ≤ 20 → 14 ≤ 20 11 + 2 ≤ 20 → 13 ≤ 20 11 + 1 ≤ 20 → 12 ≤ 20 |
Le petit café peut encore accueillir neuf personnes ou moins.
