C2. Équations et inégalités
Démontrer sa compréhension des variables, des expressions, des
égalités et des inégalités et mettre en application cette compréhension dans divers contextes.
Situation d’apprentissage : Quel problème?
Durée totale : environ 115 minutes
Sommaire
Dans cette situation d’apprentissage, les élèves représentent une équation concrètement et semi-concrètement, et rédigent une situation qui lui correspond.
| Attente | Contenus d'apprentissage |
|---|---|
| C2. Équations et inégalités Démontrer sa compréhension des variables, des expressions, des égalités et des inégalités et mettre en application cette compréhension dans divers contextes. |
C2.2 Résoudre des équations qui comprennent des nombres naturels jusqu’à 50, dans divers contextes, et vérifier les solutions. C2.3 Résoudre des inégalités qui comprennent des additions et des soustractions de nombres naturels jusqu’à 20, et vérifier et présenter les solutions à l’aide de modèles et de représentations graphiques. |
Intention pédagogique
Cette situation d’apprentissage a pour but d’amener les élèves :
- à associer une équation à une situation et à une représentation correspondante;
- à rédiger une situation qui correspond à une équation;
- à représenter une équation concrètement ou semi-concrètement.
| Contexte pédagogique | Préalables |
|---|---|
| Au cycle primaire, il importe d’initier les élèves au concept d’égalité. Les élèves déterminent la valeur inconnue, dans une équation simple, en se référant aux faits numériques d’addition et de soustraction, et représentent une équation simple à l’aide de matériel concret, de matériel semi-concret et de symboles. En 4e année, les élèves continuent à représenter des situations d’égalité de plusieurs façons et utilisent ces représentations pour résoudre des équations simples. |
Les élèves ont appris à résoudre des problèmes en effectuant des calculs pour obtenir une réponse. Dans la présente situation d’apprentissage, les élèves doivent plutôt élaborer une situation qui représente une équation donnée, sans toutefois la résoudre. Pour être en mesure de réaliser cette situation d’apprentissage, les élèves doivent :
|
Matériel
- Annexe 4.1 – Ensemble de 15 fiches (un ensemble de fiches par équipe de trois)
- boîte à chaussures
- Annexe 4.2 – Équations (photocopiée sur du papier ou du carton de couleur) (une équation par équipe de deux)
- matériel de manipulation (par exemple, cubes, matériel de base dix, balances mathématiques)
- carton ou feuille de papier de couleur
Vocabulaire mathématique
valeur inconnue, relation d’égalité, équation, symbole
Avant l’apprentissage (mise en train)
Durée : environ 45 minutes
Préparer une trousse d’algèbre pour la mise en situation. Pour ce faire, photocopier et découper les fiches de chacune des pages de l’annexe 4.1 de façon à obtenir un ensemble complet (15 fiches) par équipe de trois.
Mettre chaque ensemble de fiches pêle-mêle dans une enveloppe. Déposer toutes les enveloppes dans une boîte à chaussures.
Présenter aux élèves la situation suivante :
En faisant du rangement dans l’armoire, j’ai trouvé une trousse d’algèbre. Cette trousse contient des enveloppes qui renferment chacune 15 fiches. Sur les fiches, il y a soit l’équation, la situation ou la représentation d’une situation. J’ai besoin de votre aide pour réorganiser le contenu de chaque enveloppe. En équipes, vous devez regrouper chaque fiche Situation avec la fiche Équation et la fiche Représentation qui lui correspondent. Puisqu’il y a 15 fiches dans l’enveloppe, vous obtiendrez alors cinq regroupements de trois fiches.
S’assurer que la tâche est bien comprise en demandant à quelques élèves de l’expliquer en leurs propres mots.
Grouper les élèves en équipes de trois. Remettre un ensemble de 15 fiches à chaque équipe. Inviter les élèves à former cinq regroupements de trois fiches (situation, représentation de la situation et équation). Leur allouer suffisamment de temps pour effectuer la tâche demandée.
Note : Le but de la situation d’apprentissage est d’analyser la situation et non de résoudre un problème. En omettant la question qui est habituellement posée à la fin d’une situation (par exemple, Combien y en a-t-il en tout?), les élèves vont moins tenter d’effectuer un calcul, et leur raisonnement algébrique sera davantage sollicité. Il est donc essentiel de ne pas mettre l’accent sur la valeur inconnue.
Faire une mise en commun des regroupements qu’ont effectués les élèves en présentant les situations, une à la fois.
Faire ressortir les différents regroupements en posant aux élèves des questions telles que :
- Pourquoi avez-vous mis ces trois fiches ensemble?
- Comment savez-vous que ce regroupement est acceptable?
- Pourquoi cette représentation correspond-t-elle à cette situation et à cette équation et non pas à d’autres?
- Est-ce qu’il y a d’autres regroupements possibles?
- Quels types de représentations retrouve-t-on?
- Quelle équation représente le plus fidèlement cette situation?
- Pourquoi cette équation ne représente-t-elle pas cette situation?
Au besoin, si les élèves éprouvent de la difficulté à interpréter les représentations des situations, revoir avec elles et eux les éléments de différents modèles (par exemple, le sens de la flèche sur la droite numérique pour indiquer s’il s’agit d’un ajout ou d’un retrait, la position de la valeur inconnue sur la balance).
Note : Il est possible que certaines équipes forment des regroupements différents des autres équipes. Si une équipe
peut justifier un regroupement, il est alors accepté. Dans le regroupement A, par exemple, l’équation qui représente
le plus fidèlement la situation est 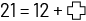 . Une équipe peut aussi présenter des arguments justifiant que l’équation
. Une équipe peut aussi présenter des arguments justifiant que l’équation 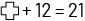 est également valable.
Toutefois, il serait impossible de justifier que l’équation
est également valable.
Toutefois, il serait impossible de justifier que l’équation  est valable, puisque la
situation donnée suppose un ajout et non un retrait. L’équation doit représenter la situation et non la stratégie
qui pourrait être utilisée pour déterminer la donnée manquante. Il importe de souligner qu’une équation respecte
plus fidèlement la situation qu’une autre, car elle suit le sens du temps et de l’action posée.
est valable, puisque la
situation donnée suppose un ajout et non un retrait. L’équation doit représenter la situation et non la stratégie
qui pourrait être utilisée pour déterminer la donnée manquante. Il importe de souligner qu’une équation respecte
plus fidèlement la situation qu’une autre, car elle suit le sens du temps et de l’action posée.
Continuer la présentation de la trousse d’algèbre en annonçant aux élèves qu’en plus des enveloppes il y a plusieurs fiches d’équations. Montrer aux élèves ces équations. Leur mentionner qu’elles et ils auront à compléter la trousse en créant une fiche Situation et une fiche Représentation de la situation correspondant à l’équation qui leur sera remise. S’assurer que la tâche à effectuer est bien comprise en demandant à quelques élèves de l’expliquer en leurs propres mots.
Pendant l’apprentissage (exploration)
Durée : environ 45 minutes
Grouper les élèves en équipes de deux. Remettre à chaque équipe une des équations de l’annexe 4.2 – Équations. Mettre à leur disposition du matériel de manipulation et des feuilles de papier brouillon.
Allouer aux élèves suffisamment de temps pour leur permettre d’accomplir la tâche. Circuler, dans la salle de classe, et observer les équipes. Inciter les élèves à réfléchir à la fidélité et à la précision de leur situation et de leur représentation. Leur poser des questions telles que :
- Pourquoi avez-vous choisi cette représentation?
- Pouvez-vous représenter cette situation autrement?
- Votre modèle respecte-t-il l’équation?
- Est-il possible d’interpréter votre modèle d’une autre façon?
- Quel élément de votre modèle permet de reconnaître qu’il représente l’équation?
| Observations possibles | Interventions possibles |
|---|---|
| Une équipe ne sait pas comment représenter l’équation. | Poser aux élèves des questions telles que : Dans les représentations de situations présentées plus tôt, y en
a-t-il une qui présente une équation semblable?
Pouvez-vous me lire l’équation et me l’expliquer en utilisant des mots? |
|
Une équipe produit une représentation pour l’équation 
|
Poser aux élèves des questions telles que : Est-ce une situation d’ajout ou de retrait? Quel élément pouvez-vous ajouter à votre dessin pour indiquer clairement l’opération effectuée? Quelle opération représentez-vous? Comment est-elle représentée? |
En partant de l’équation  , une équipe ajoute la valeur inconnue dans leur situation : Dans
l’autobus, il y a 16 bancs occupés et 9 bancs de libres. L’autobus contient au total 25 bancs. , une équipe ajoute la valeur inconnue dans leur situation : Dans
l’autobus, il y a 16 bancs occupés et 9 bancs de libres. L’autobus contient au total 25 bancs. |
Poser aux élèves des questions telles que : Dans l’équation de départ, pouvez-vous me montrer où se trouve le 9? Pourquoi y a-t-il un octogone dans l’équation? Pouvez-vous modifier la situation de façon à ne pas divulguer la valeur inconnue? |
|
Une équipe crée une représentation pour l’équation 
|
Poser aux élèves des questions telles que : Que représentent les lignes dans votre représentation? Que pourriez-vous ajouter pour montrer plus clairement la relation entre les animaux et le nombre 25? |
Distribuer aux équipes de grandes feuilles et des crayons-feutres. Inviter les élèves à y transcrire leur situation et leur représentation. Leur préciser que l’équation ne doit pas être écrite. Les inviter ensuite à afficher leur travail.
Une fois tous les travaux affichés, assigner à chaque équipe la tâche de proposer une équation qui correspond à la situation et à la représentation qu’a créées une autre équipe, de l’écrire sur un carton (préalablement distribué) et de l’apposer au bas de la feuille.
Exemple

Après l’apprentissage (objectivation et échange mathématique)
Durée : environ 25 minutes
Convier quelques équipes à justifier l’équation qu’elles ont proposée. Demander à d’autres d’expliquer la situation et la représentation qu’elles ont créées et les inviter à coller l’équation de départ sur leur feuille de travail afin de pouvoir la comparer avec celle proposée par une autre équipe.
Exemple
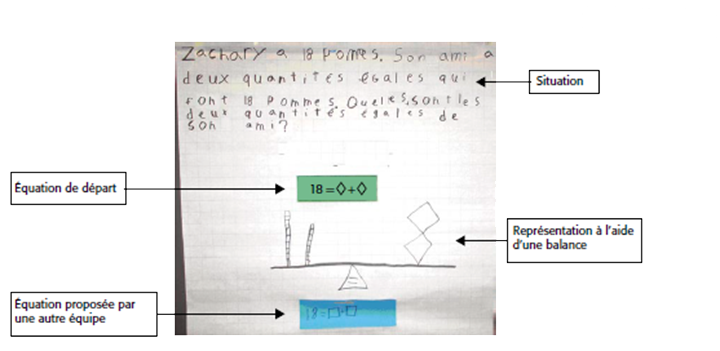
Inviter les autres élèves à contribuer à la communication et à enrichir l’échange mathématique en posant des questions ainsi qu’en faisant des observations et des interventions pertinentes. Les inciter à utiliser un vocabulaire précis.
Aider les élèves, au besoin, en leur posant des questions en fonction du contenu des travaux affichés.
Par exemple :
- Retrouve-t-on la même équation que celle du départ? Pourquoi?
- Qu’auriez-vous pu faire pour que l’équation soit respectée?
- Est-ce que la représentation est fidèle à l’équation?
- Quels éléments de la représentation vous ont permis de déterminer l’opération trouvée dans l’équation?
- Comment pourrait-on améliorer cette représentation afin qu’elle soit plus fidèle à la situation proposée?
- Comment pourrait-on améliorer cette situation afin qu’elle soit conforme à l’équation?
Tout le long de l’échange mathématique, inviter les élèves à établir des liens entre les équations en leur posant des questions qui font ressortir les ressemblances et les différences entre elles; par exemple :
- Remarquez-vous des ressemblances entre certaines équations de départ? Lesquelles?
- En quoi les équations sont-elles différentes?
Voici des possibilités de regroupements et des justifications d’élèves.
Regroupement 1

- Les nombres sont les mêmes.
- La position du symbole est différente, mais sa valeur est la même.
- Trois équations représentent une somme et deux équations représentent une différence.
- Les symboles sont différents, mais la valeur inconnue est la même.
- Il est possible de montrer la propriété de commutativité en comparant la première et la troisième équation.
Regroupement 2

- Les quantités sont les mêmes.
- La position du symbole est différente, mais sa valeur est la même.
- La dernière équation ressemble aux autres, car 12 plus 4, c’est la même chose que 16.
Regroupement 3

- Les deux équations représentent une somme.
- Dans la première équation, les symboles sont les mêmes, donc la valeur inconnue doit être la même. Cependant, dans la deuxième équation, les symboles sont différents, donc leur valeur devrait être différente, mais il est possible que leur valeur soit la même.
Différenciation pédagogique
L’activité peut être modifiée pour répondre aux différents besoins des élèves.
| Pour faciliter la tâche | Pour enrichir la tâche |
|---|---|
|
|
Suivi à la maison
À la maison, les élèves peuvent créer une équation comportant une addition ou une soustraction et utiliser des objets familiers pour la représenter concrètement.
Exemple
Équation créée : 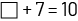
Représentation possible : une tasse pour représenter le symbole et des pâtes alimentaires pour représenter les quantités connues.

Les élèves peuvent ensuite représenter l’équation à l’aide d’une illustration et expliquer à un membre de la famille la relation entre la représentation concrète, la représentation semi-concrète et l’équation. Le lendemain, le personnel enseignant invite quelques élèves à présenter leur équation et sa représentation concrète ou semi-concrète, et anime un échange avec le groupe-classe.
Source : Guide d’enseignement efficace des mathématiques de la 4e à la 6e année, p. 123-131.

 qui ne montre
pas
clairement le retrait dans l’équation.
qui ne montre
pas
clairement le retrait dans l’équation.
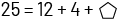 qui ne
montre pas de façon claire la relation entre les quantités qui se trouvent de chaque côté du signe
d’égalité.
qui ne
montre pas de façon claire la relation entre les quantités qui se trouvent de chaque côté du signe
d’égalité.
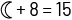 );
);
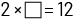 )
)