C1.3 Déterminer et utiliser des règles pour prolonger des suites, faire et justifier des prédictions, et trouver des termes manquants dans des suites à motif répété et des suites croissantes et décroissantes.
Activité 1 : la suite décroissante
Voici une table de valeurs qui résume le nombre de rectangles et de cercles que comporte chaque figure selon leur rang.
| Rang | Nombre de rectangles | Nombre de cercles |
|---|---|---|
| 1 | 32 | 40 |
| 2 | 29 | |
| 3 | 26 | 32 |
| 4 | 28 | |
| 5 | ||
| 6 | 17 |
Demander aux élèves de trouver la règle et ainsi déterminer les nombres manquants dans la table de valeurs.
Poser des questions aux élèves telles que:
- Quels sont les changements observés dans les figures lors du passage d’un rang à l’autre? Explique ton raisonnement.
- À quoi te servent les règles? Justifie ta réponse.
- À quoi ressemble la figure au rang 0? À quoi ressemble la figure au 5e rang? Comment le sais-tu?
- Selon toi, à quoi ressemblera la figure au 10e rang? Vérifie ta prédiction.
- Selon toi, est-il possible de construire un terme de cette suite qui comporte exactement 2 rectangles et aucun cercle? Comment le sais-tu?
Activité 2 : un carré, des carrés
Présenter aux élèves la suite ci-dessous et leur demander de tracer le quatrième dallage.
Inviter les élèves à déterminer la règle et à l’utiliser afin de tracer le cinquième dallage. Leur demander ensuite de créer une table de valeurs qui représente la relation entre le rang du dallage et le nombre de carrés qui le composent.
| Rang de dallage | 1 | 2 | 3 | 4 | 5 | 6 |
|---|---|---|---|---|---|---|
| Nombre de carrés | 1 | 4 | 9 | 16 | 25 | ? |
Afin d’amener les élèves à analyser la relation entre le rang du dallage et le nombre de carrés qui le composent, poser des questions telles que :
- Quel est le prochain nombre de carrés à inscrire dans le tableau? Comment l’avez-vous déterminé?
- Peut-on créer un tel dallage avec 15 carrés? 49 carrés? 81 carrés? 50 carrés? Expliquez votre réponse.
- Dans cette suite, comment peut-on déterminer le nombre de carrés requis pour créer un dallage quelconque?
- Combien de carrés composeront le 10e dallage? le 12e dallage? le 20e dallage?
- Qu’est-ce que tous les nombres de carrés ont de particulier?
- Quelle est la relation entre le rang du dallage et le nombre de carrés?
Afin d’amener les élèves à reconnaître que le nombre de carrés qui composent un dallage correspond toujours au carré du rang du dallage (ou à l’aire du dallage), lire les valeurs de la table à voix haute (6, 36; 5, 25; 4, 16…).
Inciter les élèves à examiner les dallages en fonction du nombre de rangées et de colonnes (par exemple, le 3e dallage est composé de 3 rangées de 3 carrés ou de 3 colonnes de 3 carrés) ou à penser aux faits de multiplication.
Prolongement
Inviter les élèves à examiner les ajouts de carrés dans la suite de dallages. On peut reconnaître que, d’un dallage à l’autre, on ajoute toujours un nombre impair de carrés.
Créer un tableau similaire au tableau suivant.
| Rang de dallage | 1 | 2 | 3 | 4 | 5 |
|---|---|---|---|---|---|
| Nombre de carrés par couleur | 1 carré jaune | 1 carré jaune 3 carrés bleus |
1 carré jaune 3 carrés bleus 5 carrés verts |
1 carré jaune 3 carrés bleus 5 carrés verts 7 carrés … |
… |
À l’aide de questions, amener les élèves à formuler une généralisation telle que la somme des premiers nombres impairs consécutifs est toujours un nombre carré. Leur demander ensuite de vérifier si cette généralisation s’applique aussi aux nombres pairs.
Source : Guide d’enseignement efficace des mathématiques de la 4e à la 6e année, p. 158-159.
Activité 3 : stratège
Présenter le jeu Stratège. Il se joue à deux au moyen d’une bande comme celle-ci :
Voici les règles du jeu :
- En partant de « 0 », on déplace le jeton à tour de rôle vers la droite.
- On peut avancer le jeton d’une case ou de deux cases.
- La première personne qui arrive sur la case « 8 » perd la joute.
Former des équipes de deux élèves. Remettre à chaque équipe une copie de l’annexe 5.5 (Stratège). Inviter les élèves à jouer en notant le déroulement du jeu sur l’annexe 5.5 afin de pouvoir l’analyser et déterminer des régularités dans les résultats.
Exemple
Pendant le jeu, poser la question : « Y a-t-il une stratégie qui assure la victoire? » Un peu plus tard, poser la question : « Y a-t-il une stratégie qui permet à la personne qui joue en premier de s’assurer de la victoire? » Dire aux élèves d’expliquer clairement par écrit toute stratégie gagnante.
Voici un exemple d’explication d’élève :
« Afin de gagner, le premier joueur (A) doit placer le jeton sur la case 1. Après, il contrôle le jeu. Peu importe ce que l’autre joueur (B) décide de faire, le joueur A doit se rendre à la case 4 puis à la case 7. De cette façon, le joueur B devra toujours jouer un tour en partant du 7 et se rendre au 8 et… perdre. En résumé, le joueur A peut toujours gagner s’il dépose successivement son jeton sur les cases 1, 4 et 7. »
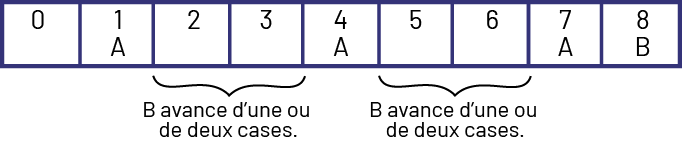
Inviter ensuite les élèves à jouer en utilisant une bande contenant un nombre différent de cases, et à vérifier si la stratégie gagnante reste la même ou si elle doit être modifiée.
Source : Guide d’enseignement efficace des mathématiques de la 4e à la 6e année, p. 160-161.
Activité 4 : une régularité, plusieurs relations
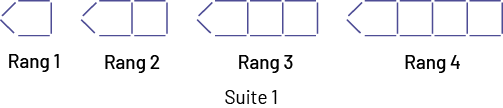
Indiquer aux élèves qu’on s’intéresse à la relation entre le rang de la figure et le nombre de cure-dents qui le composent. Inviter les élèves à analyser la suite de figures, à prolonger la suite, à créer une table de valeurs qui représente la relation, à déterminer le nombre de cure-dents dans une figure lointaine (par exemple, la 10e) et à formuler une règle.
(D’après la table de valeurs, le nombre de cure-dents augmente de 3 chaque fois. On peut le voir dans la suite non
numérique, car pour passer d’un rang au suivant, il faut ajouter 3 cure-dents, soit 
).
Exemple de règle pour la suite 1
Chaque figure est composée de 2 cure-dents et de l’ajout de groupes de 3 cure-dents. Le nombre de ces groupes correspond au rang de la figure.
La figure au 10e rang sera donc composée de 2 cure-dents et de 10 fois l’ajout de 3 cure-dents (30), soit de 32 cure-dents.
Répéter la même démarche avec les deux suites suivantes :
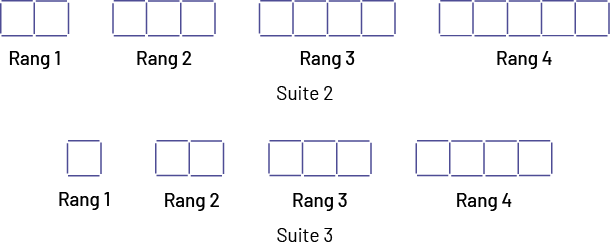image Suite
non numérique à motifs croissants.Rang un : 7 cure-dents.Rang 2 : dix cure-dents.Rang 3 : 13 cure-dents.Rang 4 : 16
cure-dents.Suite non numérique à motifs croissants.Rang un : 4 cure-dents.Rang 2 : 7 cure-dents.Rang 3 : 10
cure-dents.Rang 4 : 13 cure-dents.
Ensuite, inviter les élèves à comparer les trois situations et les règles qui représentent la relation entre le rang de la figure et le nombre de cure-dents qui le composent. Les amener à reconnaître que les trois situations présentent la même règle (une figure est toujours formée en ajoutant, de la même façon, 3 cure-dents à la figure du rang précédent), mais que les relations diffèrent parce que les motifs de base (Rang 1) sont différents.
Exemple de règle pour la suite 2
Chaque figure est composée de 4 cure-dents et de l’ajout de groupes de 3 cure-dents. Le nombre de ces groupes correspond au rang de la figure.
La figure au 10e rang sera donc composée de 4 cure-dents et de 10 fois l’ajout de 3 cure-dents (30), soit de 34 cure-dents.
Exemple de règle pour la suite 3
Chaque figure est composée de 1 cure-dent et de l’ajout de groupes de 3 cure-dents. Le nombre de ces groupes correspond au rang de la figure.
La figure au 10e rang sera donc composée de 1 cure-dent et de 10 fois l’ajout de 3 cure-dents (30), soit de 31 cure-dents.
Ensuite, inviter les élèves à décrire les suites numériques qui se rattachent aux situations.
Exemple de réponses
Suite 1 : Pour reproduire la suite, on commence par 5, puis on ajoute toujours 3 (5, 8, 11, 14, 17…).
Suite 2 : Pour reproduire la suite, on commence par 7, puis on ajoute toujours 3 (7, 10, 13, 16, 19…).
Suite 3 : Pour reproduire la suite, on commence par 4, puis on ajoute toujours 3 (4, 7, 10, 13, 16…).
Source : Guide d’enseignement efficace des mathématiques de la 4e à la 6e année, p. 161-163.