C1. Suites et relations :
Reconnaître, décrire, prolonger et créer une variété de suites, y compris des suites trouvées dans la vie quotidienne, et faire des prédictions à leur sujet.
Situation d’apprentissage : location de films
Durée approximative : 150 minutes
Sommaire
Dans cette situation d’apprentissage, les élèves résolvent une situation-problème de la vie courante qui fait appel au concept de relation. Les élèves utilisent diverses stratégies pour déterminer une règle définissant une relation donnée et l’expliquent verbalement.
| Attentes | Contenus d’apprentissage |
| C1. Algèbre Reconnaître, décrire, prolonger et créer une variété de suites, y compris des suites trouvées dans la vie quotidienne, et faire des prédictions à leur sujet. |
C1.1 reconnaître et décrire des suites à motif répété ainsi que des suites croissantes et
des suites décroissantes, y compris des suites trouvées dans la vie quotidienne.
C1.2 créer des suites croissantes et des suites décroissantes, à l’aide d’une variété de représentations, y compris des tables de valeurs et des représentations graphiques, et établir des liens entre les différentes représentations. C1.3 déterminer et utiliser des règles pour prolonger des suites, faire et justifier des prédictions, et trouver des termes manquants dans des suites à motif répété et des suites croissantes et décroissantes. C1.4 créer et décrire des suites numériques comprenant des nombres naturels, des nombres décimaux jusqu’aux dixièmes et des nombres décimaux jusqu’aux centièmes, et représenter des relations entre les nombres. |
Intention pédagogique
Cette situation d’apprentissage a pour but d’amener les élèves :- à représenter de différentes façons la relation correspondant à une situation donnée;
- à communiquer en mots la règle qui définit cette relation.
| Contexte pédagogique | Préalables |
| Au cycle primaire, les élèves ont appris à repérer et à décrire une règle de régularité dans une suite non numérique et dans une suite numérique. En 3e année, elles et ils représentent, à l’aide de tables de valeurs, des relations simples correspondant à diverses situations. En 5e année, les élèves poursuivent l’étude des relations et apprennent à les définir à l’aide de règles exprimées en mots. | La présente situation d’apprentissage permet aux élèves de faire appel à différentes représentations d’une
relation. Le passage d’une représentation à une autre facilite l’analyse de la relation et aide les élèves à
l’expliquer.
Pour être en mesure de réaliser cette situation d’apprentissage, les élèves doivent pouvoir :
L’annexe 5.4 (Activité préparatoire facultative : Suite non numérique croissante) permet aux élèves de consolider certains concepts liés aux suites non numériques croissantes. S’en servir, au besoin, pour vérifier si les élèves ont acquis les préalables nécessaires à la réalisation de la présente situation d’apprentissage. |
Matériel
- cubes emboîtables (environ 1 000)
- annexe 5.1A et annexe 5.1B (une copie par équipe)
- marqueurs de bingo (un par équipe)
- annexe 5.2 (une copie par équipe)
- annexe 5.3
- annexe 5.4
Note : L’annexe ne représente pas tout à fait la situation d’apprentissage. Le personnel enseignant peut l’adapter en mentionnant qu’il s’agit d’un service de location de film en ligne.
Vocabulaire mathématique
règle de régularité, règle de correspondance, relation, suite numérique, suite non numérique, table de valeurs
Avant l’apprentissage (mise en train)
Durée approximative : 60 minutes
Revoir avec les élèves le concept de relation et certaines de ses représentations à l’aide de la situation suivante.
Poser aux élèves les questions suivantes :
- Si Dimitri et Anouka louent cinq films, combien cela leur coûte-t-il? Pourquoi?
- Après avoir loué 17 films, combien auront-ils dépensé? Qu’avez-vous fait pour déterminer ce montant?
Ensuite, créer avec les élèves une table de valeurs qui représente la relation entre le nombre de films loués et le montant déboursé en dollars.
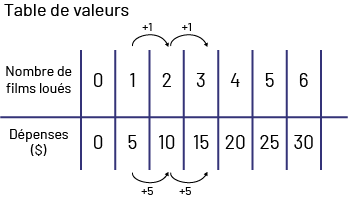
Inciter les élèves à analyser les relations entre les nombres en posant des questions telles que :
- Si vous examinez la rangée intitulée « Nombre de films loués » dans la table de valeurs, que constatez-vous? (D’une colonne à l’autre, il y a toujours un film de plus que dans la colonne précédente. Donc, il y a une règle de régularité de + 1.)
- Si vous examinez la rangée intitulée « Dépenses ($)» dans la table de valeurs, que constatez-vous? (D’une colonne à l’autre, il y a toujours 5 $ de plus que dans la colonne précédente. Donc, il y a une règle de régularité de + 5.)
- Quelle relation remarquez-vous entre le nombre de films loués et le montant déboursé? (Le montant déboursé est toujours cinq fois plus grand que le nombre de films loués.)
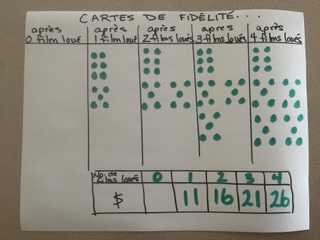
Mentionner aux élèves que le site de location de films offre une carte de fidélité virtuelle à sa clientèle. Préciser qu’un point est attribué à la carte pour chaque dollar dépensé.
Montrer, au groupe-classe, la carte de fidélité d’une personne qui n’a pas encore loué de film et celle de personnes qui ont loué respectivement un, deux, trois et quatre films. La photo ci-dessous illustre deux exemples de séries de cartes de fidélité représentant le montant déboursé en fonction du nombre de films loués. Ainsi, après la location d’un film au coût de 5 $, il y a cinq points sur la carte, après la location d’un deuxième film, il y en a 10 et ainsi de suite.

Note : La suite non numérique croissante ainsi créée par les représentations des cartes de fidélité permet de repérer plus facilement la règle de correspondance. Il est important de commencer la suite par la représentation d’une carte de fidélité sans aucune location de film, car dans les situations subséquentes, certains sites de location de films exigeront un coût d’abonnement avant de pouvoir louer un film.
Amener les élèves à verbaliser une règle qui définit cette relation en posant des questions telles que :
- Pouvez-vous décrire la carte de fidélité d’une cliente qui a loué 12 films?
- Combien la cliente a-t-elle dépensé sur ce site de location de films?
- Après avoir loué 20 films, combien une personne a-t-elle dépensé?
- Qu’avez-vous fait pour trouver la réponse?
- Pouvez-vous trouver une façon rapide de déterminer le montant déboursé, peu importe le nombre de films loués?
Voici un exemple d’une règle de correspondance exprimée en langage courant par une élève : « Après la location de 20 films, il y aura 20 colonnes de 5, donc 100 points, sur la carte de fidélité. Chaque point représente 1 $ déboursé. Alors, on multiplie toujours par 5. »
Afin d’aider cette élève à préciser sa pensée et à exprimer clairement sa règle de correspondance, poser des questions telles que :
- Qu’est-ce qu’on multiplie par 5? (Le nombre de films loués)
- En multipliant le nombre de films loués par 5, qu’est-ce qu’on obtient? (Le montant déboursé)
L’élève peut alors exprimer une règle plus précise : « Lorsque je multiplie le nombre de films loués par 5, j’obtiens le montant déboursé. »
Expliquer aux élèves que, lorsqu’on décrit une façon rapide de déterminer la valeur d’un terme quelconque (par exemple, le montant déboursé) dans une suite, on exprime une règle définissant une relation entre le rang et les termes de la suite.
Former des équipes de deux élèves. Remettre une copie des annexes 5.1A et 5.1B à chaque équipe et lire à voix haute la situation suivante:
Lire aussi les questions présentées à l’annexe 5.1A et s’assurer que les élèves saisissent bien la tâche à accomplir.
Note : L’avantage pour les élèves de commencer, à la question 1, avec une représentation concrète de la situation plutôt qu’avec une représentation semi-concrète telle qu’un dessin, c’est de pouvoir réorganiser rapidement le matériel en cas d’erreur au lieu d’avoir à effacer ou de tout recommencer. La plupart des élèves ne rencontreront aucune difficulté à représenter la suite de cartes de fidélité pour les films loués, mais certaines et certains auront tendance à oublier de représenter la carte de fidélité sans film loué. Les amener à reconnaître qu’un abonnement de 4 $ est exigé et qu’elles et ils doivent représenter une carte de fidélité comprenant seulement ce montant.
Inviter les équipes à effectuer la tâche. Observer leur travail et intervenir au besoin. Veiller particulièrement à ce que les élèves créent une suite non numérique croissante qui montre clairement la régularité dans cette situation.
Au besoin, poser des questions telles que :
- Est-ce que l’ajout des cubes (jetons, tampons…) s’effectue toujours de la même façon et dans le même ordre?
- Qu’y a-t-il de semblable d’une carte à l’autre dans la suite que vous avez créée?
- Qu’y a-t-il de différent d’une carte à l’autre?
- Quelle est la règle de régularité de cette suite?
- Combien y a-t-il de points accordés sur la carte de fidélité quand aucun film n’est loué? Pourquoi?
Voici quelques exemples de travaux d’élèves.
- Cette équipe a représenté le montant déboursé après la location d’un film, soit 9 $, par un groupe de quatre cubes et un groupe de cinq cubes. Puis, elle a ajouté successivement cinq cubes dans chacune des représentations subséquentes. Toutefois, elle n’a rien placé sous l’étiquette « Carte de fidélité après 0 film loué ».

- Cette équipe a simplement établi une correspondance entre chaque montant déboursé et le nombre de cubes utilisés pour la représenter, sans se préoccuper de leur disposition. Puisque la suite créée n’est pas croissante, on ne peut repérer facilement l’ajout de cinq cubes d’une représentation à l’autre. Il est donc plus difficile de décrire la règle de régularité et d’élaborer une règle de correspondance qui définit la relation entre le nombre de films loués et le montant déboursé.

- Cette équipe a organisé le matériel de manipulation en respectant la régularité, créant ainsi une suite non numérique concrète. Elle a ensuite produit une suite non numérique semi-concrète de cartes de fidélité à l’aide d’un marqueur de bingo. En créant ces deux suites, cette équipe a représenté la situation de façon claire et précise. Il sera alors plus facile d’élaborer une règle correspondant à cette situation.

Lorsque les équipes ont terminé la tâche (annexe 5.1A), demander à quelques équipes d’afficher leur suite de cartes de fidélité. En groupe-classe, revoir les questions en vérifiant la pertinence des suites affichées.
Inciter les élèves à comparer les deux sites de location de films et à formuler une règle de correspondance pour chacune des situations en posant des questions telles que :
- Quel est le coût de location de cinq films dans chacun des sites? (Sur le premier site, le coût est de 25 $ (5 films × 5 $) et sur le deuxième site, il est de 29 $, car on doit ajouter le coût de l’abonnement de 4 $.)
- Qu’est-ce qui est semblable entre les deux sites? différent? (Ce qui est semblable, c’est le coût de location de 5 $ par film. Ce qui est différent, c’est la présence ou l’absence d’un coût d’abonnement de 4 $.)
- Comment pourrions-nous déterminer rapidement le montant déboursé selon le nombre de films loués sur chaque site? (Pour déterminer rapidement le montant déboursé sur le premier site, on multiplie le nombre de films loués par 5 tandis que pour le deuxième site, on multiplie aussi le nombre de films loués par 5, puis on ajoute le coût de l’abonnement de 4 $.)
Note : Il est important de reconnaître qu’une règle de correspondance peut être exprimée différemment par les élèves selon leur perception de la relation.
Pendant l’apprentissage (exploration)
Durée approximative : 70 minutes
Préparer les cinq scénarios ci-dessous en inscrivant les caractéristiques de chacun dans les cases appropriées des copies de l’annexe 5.2 (Nouveau club vidéo).
| Scénario | Coût de l'abonnement | Coût de la location par film |
|---|---|---|
| 1 | 5 $ | 4 $ |
| 2 | 0 $ | 6 $ |
| 3 | 5 $ | 6 $ |
| 4 | 6 $ | 5 $ |
| 5 | 50 $ | 2 $ |
Présenter la situation suivante :
Former des équipes de deux élèves. Remettre un scénario à chaque équipe. S’assurer de répartir les cinq scénarios entre les équipes. Expliquer les composantes du rapport à soumettre à l’entreprise, soit :
- un exemple d’une suite de cartes de fidélité correspondant à la location d’aucun film, d’un film, de deux films, de trois films et de quatre films en n’oubliant pas d’inclure le coût de l’abonnement s’il y a lieu;
- une table de valeurs qui représente la relation entre le nombre de films loués et la somme dépensée;
- l’énoncé en mots d’une règle de correspondance qui permet de déterminer rapidement le montant déboursé par une cliente ou un client en fonction du nombre de films loués;
- un nom pour le nouveau site de location de films.
Inviter les équipes à accomplir la tâche. Circuler parmi les élèves et intervenir au besoin. Porter une attention particulière à la façon dont les élèves organisent les éléments (points) sur les cartes de fidélité.
| Observations possibles | Interventions possibles |
| Une équipe n’arrive pas à organiser les points sur les cartes de fidélité. | Suggérer de représenter d’abord la situation avec du matériel concret.
Poser ensuite des questions telles que :
|
| Une équipe qui a le scénario 1 a oublié de tenir compte du coût de l’abonnement (5 $) et a représenté uniquement le coût de la location des films (4 $ par film loué). | Poser des questions telles que :
|
|
Une équipe qui a le scénario 4 organise les points sans créer de suite non numérique croissante. La quantité est respectée, mais l’organisation ne permet pas de voir facilement l’ajout de cinq points d’une carte à l’autre. |
Amener les élèves à reconnaître que les points doivent être ajoutés dans un ordre précis en posant des questions telles que :
|
| Une équipe qui a représenté correctement le scénario n’arrive pas à communiquer une règle de correspondance en mots. | Inciter les élèves à analyser leur représentation du scénario (table de valeurs ou la suite de cartes de
fidélité) en posant des questions telles que :
|
Demander aux équipes d’afficher les composantes de leur rapport sur une grande feuille (voir l’annexe 5.3 pour des exemples de rapport). Assigner à chaque équipe un type de présentation à suivre (voir Types de présentations ci-après). Allouer le temps nécessaire pour leur permettre d’élaborer une présentation claire et précise. Une fois la tâche accomplie, demander aux équipes d’afficher leur rapport aux murs de la classe.
Après l’apprentissage (objectivation/échange mathématique)
Durée approximative : 20 minutes
Inviter quelques équipes à venir, à tour de rôle, présenter leur rapport.
Types de présentations
Certaines équipes peuvent présenter leur rapport en donnant des explications sur leur démarche. Voici quelques exemples d’explications d’élèves :
- Lorsque nous avons reçu notre scénario, nous savions que, pour aucun film loué, il y aurait quand même une somme dépensée parce qu’il y a un abonnement à payer.
- Puisque le prix de location est de 6 $ par film, alors on sait que pour chaque film loué, on devra débourser 6 $ et ajouter six points sur la carte de fidélité.
- Au début, on a mis les points n’importe comment sur les cartes, puis on s’est rendu compte qu’il était difficile de voir la règle. On a donc refait les cartes en réorganisant les points pour mieux la voir.
- En examinant notre suite de cartes de fidélité, on peut remarquer la présence d’un coût d’abonnement et l’ajout de six points d’une carte à l’autre puisque, selon notre scénario, chaque film coûte 6 $.
Note : L’élève appuie ses explications en utilisant la suite de cartes de fidélité.
Certaines équipes peuvent présenter leur rapport en posant des questions d’interprétation telles que :
- Est-ce que quelqu’un peut nous dire combien coûte la location d’un film sur ce site?
- Parmi les sites affichés au tableau, est-ce qu’il y en a un qui présente la même situation que la nôtre? Lequel et pourquoi?
- Pouvez-vous nous dire si ce site exige un abonnement? Si oui, combien coûte-t-il?
- À l’aide de la suite de cartes de fidélité ou de la table de valeurs, qui peut nous dire de quoi aurait l’air la carte après 15 films loués sur ce site?
- Quelqu’un peut-il expliquer, dans ses mots, une règle de correspondance qui définit la relation entre le nombre de films loués et la somme dépensée sur ce site?
D’autres équipes peuvent présenter leur rapport en cachant certains éléments, par exemple, la carte de fidélité affichant 0 film loué et le terme sous le 0 dans la table de valeurs (voir la photo ci-dessous). En posant des questions, les membres de l’équipe amènent les autres élèves à déterminer les éléments cachés et à établir la règle qui définit la relation dans ce scénario.
Inciter les élèves à réagir à chacune des présentations et à faire part de leurs observations ou de leurs questions. Faciliter le déroulement de l’échange mathématique en posant au besoin des questions telles que :
- Lorsque vous avez reçu votre scénario, par quel modèle de représentation avez-vous commencé (matériel de manipulation, tampons, table de valeurs)?
- Qui peut expliquer dans ses mots la disposition des points sur les cartes de fidélité qu’on vient de présenter?
- Est-ce que vous avez utilisé du matériel de manipulation avant de représenter votre scénario sur des cartes de fidélité? Si oui, est-ce que cela vous a facilité la tâche?
- Ces deux équipes avaient le même scénario, mais leurs cartes de fidélité sont différentes. Comment peut-on justifier qu’elles représentent bel et bien ce scénario?
- Selon le scénario qu’on vient d’examiner, de quoi aurait l’air la carte de fidélité après six films loués? dix films loués?
- Comment s’y prend-on pour déterminer le nombre de points sur d’autres cartes de fidélité? Quelle règle définit la relation dans ce scénario?
Différenciation pédagogique
L’activité peut être modifiée pour répondre aux différents besoins des élèves.
| Pour faciliter la tâche | Pour enrichir la tâche |
|
|
Suivi à la maison
À la maison, les élèves font part de la situation d’apprentissage vécue en classe à une ou à un membre de leur famille, puis présentent les tables de valeurs ci-dessous. Ensemble, elles et ils comparent les coûts et déterminent une règle qui définit la relation entre le nombre de films loués et la somme dépensée sur chaque site afin de répondre aux questions suivantes :
- Quel site est le plus avantageux pour quelqu’un qui loue sept films? (Le site 1)
- Quel site est le plus avantageux pour quelqu’un qui loue 20 films? (Le site 2)
Site 1
| Nombre de films loués | 0 | 1 | 2 | 3 | 4 | 5 |
|---|---|---|---|---|---|---|
| Montant déboursé ($) | 0 | 6 | 12 | 18 | 24 | 30 |
Site 2
| Nombre de films loués | 0 | 1 | 2 | 3 | 4 | 5 |
|---|---|---|---|---|---|---|
| Montant déboursé ($) | 30 | 32 | 34 | 36 | 38 | 40 |
Source : Guide d’enseignement efficace des mathématiques de la 4e à la 6e année, p. 145-157.
