C3. Mettre en application ses habiletés en codage pour résoudre des problèmes et créer des représentations de situations mathématiques de façons computationnelles, à l’aide de concepts et d’habiletés en codage.
Situation d’apprentissage : la machine à probabilité
Durée approximative : 125 minutes
Sommaire
Dans cette situation d’apprentissage, l’élève crée une machine à utiliser le lancer aléatoire d’un dé afin de montrer que plus le nombre d’essais est élevé, plus la probabilité expérimentale se rapproche de la probabilité théorique.
| Attentes | Contenus d'apprentissage |
| C3. Algèbre Résoudre des problèmes et créer des représentations de situations mathématiques de façon computationnelle à l’aide de concepts et d’habiletés en codage. |
C3.1 Résoudre des problèmes et créer des représentations de situations mathématiques de
façon computationnelle en écrivant et en exécutant des codes, y compris des codes comprenant des instructions
conditionnelles et d’autres structures de contrôle.
C3.2 Lire et modifier des codes donnés, y compris des codes comprenant des instructions conditionnelles et d’autres structures de contrôle, et décrire l’incidence de ces changements sur les résultats. |
| D2. Données Décrire la probabilité que des événements se produisent et utiliser cette information pour faire des prédictions. |
D2.2 Déterminer et comparer les probabilités théoriques et expérimentales qu’un événement se produise. |
| Pratiques pédagogiques à fort impact en mathématiques à privilégier | Description |
| Résultats d’apprentissage, critères d’évaluation et rétroaction descriptive | Affichez, dans la salle de classe, les critères d’évaluation pour que les élèves s’y réfèrent pendant leur travail. Tout le long de la leçon, prendre le temps de circuler parmi les élèves et d’observer ce qu’elles et ils font. En profiter pour les interroger sur leur travail et leur donner une rétroaction descriptive relative aux critères d’évaluation affichés. |
| Conversations mathématiques | Dans la mise en situation, les élèves discutent des probabilités possibles en lançant le dé. Pendant leur exploration des résultats possibles, elles et ils écoutent les différentes opinions et expliquent leur raisonnement à leurs pairs. Prendre le temps de circuler parmi les élèves et les questionner au sujet de ce qu’elles et ils remarquent, de ce qu’elles et ils connaissent ou de ce qu’elles et ils aimeraient connaître. |
| Regroupements flexibles | Les élèves travaillent en groupe afin de favoriser la collaboration. Les expériences en petits groupes sécurisent les élèves et les motivent souvent à prendre des risques. Elles et ils peuvent travailler en petits groupes pour créer leur machine à probabilité qui facilitera, en temps et en précision, les 1 000 lancers demandés. |
|
Connaissances et habiletés préalables |
|---|
|
Pour être en mesure de réaliser cette situation d’apprentissage, l’élève doit :
|
Résultats d’apprentissage
À la fin de cette situation d’apprentissage, l’élève pourra :
- écrire et exécuter le code d’un lancer de dé aléatoire dans un logiciel de programmation par blocs;
- intégrer une ou des instructions conditionnelles dans son code;
- comparer les probabilités théoriques et expérimentales d’un événement.
Critères d’évaluation selon les grilles d’évaluation du rendement
| Compétences | Critère(s) d’évaluation |
|---|---|
| Connaissance et compréhension |
|
| Habiletés de la pensée |
|
| Communication |
|
| Mise en application |
|
Matériel requis
- logiciel de programmation par blocs
- dés numérotés de 1 à 6
- annexe A (tableau dans lequel compiler les résultats expérimentaux)
- crayon
- annexe -Dés
Vocabulaire mathématique
probabilité expérimentale, probabilité théorique, événements répétitifs, événements imbriqués, instruction conditionnelle, structure de contrôle
Mise en situation
Durée approximative : 10 minutes
L’évaluation peut se faire par les…
En groupe-classe, montrer l’image des dés. Demander aux élèves de trouver des questions à se poser relativement à cette image.

Exemples de questions :
- Combien de points y a-t-il en tout?
- Combien de fois voit-on le nombre 6?
- Quelle est la probabilité d’obtenir un 3?
Grouper les élèves en petits groupes et remettre un dé numéroté de 1 à 6 à chacun. Leur demander de trouver la probabilité théorique d’obtenir un nombre pair. Au besoin, revoir la ligne de probabilité et la terminologie associée.

Exemple de réflexion recherchée :
- Il y a trois nombres pairs, soit 2, 4 et 6. Il y a six résultats possibles lorsqu’on lance un dé. La probabilité d’avoir un nombre pair est donc de \(\frac{3}{6}\).
- La fraction \(\frac{3}{6}\) peut être simplifiée à \(\frac{1}{2}\) , qui représente aussi la moitié. Sur la ligne de probabilité, cela nous indique qu’il est équiprobable que l’on obtienne un nombre pair ou un nombre impair.
| Observation possible | Pistes d’intervention |
| L’élève ne sait pas par où commencer. | Que dois-tu faire en premier?
Quels sont tous les résultats possibles à la suite d’un lancer de dé? Quels sont les nombres pairs sur le dé? Qu’est-ce qu’une probabilité? |
| L’élève a de la difficulté à exprimer une probabilité sous forme de fraction. | Que représente le numérateur en probabilité?
Que représente le dénominateur en probabilité? Combien de côtés le dé a-t-il au total? Ce total représente-t-il le numérateur ou le dénominateur? |
| L’élève a de la difficulté à exprimer la probabilité d’obtenir un nombre pair sous forme de fraction. | Que représente la fraction \(\frac{3}{3}\) ? (un entier, \(\frac{1}{1}\) ou 100 %)
Est-ce vrai que chaque lancer du dé aboutira à un nombre pair? |
Demander aux élèves de trouver la probabilité théorique d’obtenir un multiple de 3, puis la probabilité d’obtenir le nombre 4. Les élèves devront ensuite placer les probabilités sur la ligne de probabilité, comme dans le premier exemple.
Exemples de réflexion recherchée :
- Il y a deux multiples de 3 sur un dé à six faces (3 et 6), et six résultats possibles, donc la probabilité d’obtenir un multiple de 3 est de \(\frac{2}{6}\).
- La fraction \(\frac{2}{6}\) est équivalente à \(\frac{1}{3}\).
Ou
- Je sais que \(\frac{1}{3}\) se situe entre \(\frac{1}{4}\) et \(\frac{1}{2}\).
- Il y a un seul nombre 4 sur un dé à six faces, et six résultats possibles, donc la probabilité d’obtenir un 4 est de \(\frac{1}{6}\).
Demander aux élèves de lancer le dé 20 fois et de compiler les résultats dans un tableau de fréquences relatives comme celui-ci.
| Événement | Dénombrement | Fréquence | Fréquence relative exprimée en fraction |
| J’obtiens un nombre pair. | |||
| J’obtiens un multiple de 3. | |||
| J’obtiens un 4. |
Demander aux élèves ce que l’on remarque dans les résultats obtenus.
Les résultats représentent-ils la probabilité théorique? Pourquoi? (Écrire les réponses des élèves à cette question pour s’y référer plus tard.)
Discuter des résultats obtenus et les comparer avec les probabilités trouvées plus tôt. Encourager les élèves à se questionner sur l’effet du nombre de lancers sur le résultat.
Déroulement
Durée approximative : 100 minutes
L’évaluation peut se faire par les…
Demander aux élèves de déterminer la probabilité expérimentale d’obtenir un nombre pair en lançant le dé 1 000 fois.
Exemple de réflexion recherchée :
- 1000 lancers de dé, c’est beaucoup, et ça prendra beaucoup de temps.
- Un lancer de dé dure environ 5 secondes, donc 1000 lancers équivalent approximativement à 5000 secondes (5000 secondes, c’est environ 83 minutes!).
- Avec autant de lancers, on pourrait faire plus d’erreurs, par exemple oublier de mettre un résultat dans le tableau de fréquences ou perdre le compte du nombre de lancers.
Questionner les élèves à savoir s’il y a une façon plus efficace de déterminer les résultats de 1000 lancers (on cherche à nommer le code comme outil de représentation).
Demander d’abord aux élèves ce que devrait faire l’ordinateur pour compter le nombre de fois où l’on obtient un nombre pair après 1 000 lancers d’un dé à six faces. Cela deviendra le pseudocode qui dirigera le codage par blocs.
Exemple de pseudocode :
|
Répéter 1 000 fois. |
|
Générer un nombre aléatoire de 1 à 6. |
|
Ajouter le nombre à la liste « La liste des lancers ». |
|
Si le nombre = 2 ou le nombre = 4 ou le nombre = 6. |
|
ajouter 1 au compteur « Nombres pairs ». |
Le code est constitué de trois parties :
- Une séquence de code pour lancer un dé à six faces et compiler les résultats.
- Une séquence de code avec un événement conditionnel visant de déterminer si le résultat du lancer est pair ou non.
- Une séquence de code qui compilera le total des lancers aboutissant à un nombre pair.
Voici un exemple de code qui détermine le nombre de fois où l’on obtient un nombre pair à la suite des 1000 lancers du dé, basé sur le pseudocode ci-dessus.
image Un bloc de codage commençant par un bloc de contrôle qui montre « quand » un drapeau vert « est cliqué ». Empilé sur le bloc variable suivant qui montre le mot « mettre » puis « Nombres pairs » avec une flèche vers le bas, à côté de cela « à » « Zéro » dans une bulle. Empilé sur le bloc de variables suivant qui affiche le mot « mettre » puis « le numéro du lanceur » avec une flèche vers le bas, à côté de ce « à » « Zéro » dans une bulle. Le bloc suivant est un bloc de correction marqué « supprimer tous les éléments de la liste » avec une bulle marquée « La liste des lanceurs » et une flèche vers le bas. La séquence de répétition commence ensuite par un bloc de contrôle qui affiche « répéter », « mille » dans un cercle suivi du mot « fois ». Des blocs variables sont intégrés dans ce bloc. Le bloc marqué « mettre » puis « Face du dé » avec une flèche vers le bas, à côté de cela « à » et une plage qui se lit « nombre aléatoire entre » avec « un » dans une bulle et « et » « 6 » dans l'autre bulle. Le tout est empilé sur un bloc marqué « ajouter » et « face du dé » dans une bulle « à » « La liste des lanceurs » avec une flèche vers le bas. Ce bloc présente une flèche qui part du bas dans le sens inverse des aiguilles d'une montre. Le bloc de répétition suivant commence par le bloc marqué « répéter » et « longueur de » « La liste des lancers » ainsi qu'une flèche descendante et le mot « fois ». Il est empilé sur une séquence conditionnelle marquée par le bloc « si ». Elle contient deux variables marquées « élément » puis « le numéro du lanceur » dans une bulle « de » « La liste des lanceurs » avec une flèche descendante égale « 2 » dans une bulle ou « élément » puis « le numéro du lanceur » dans une bulle « de » « La liste des lancers » avec une flèche descendante égale « 4 » dans une bulle ou « élément » alors « le numéro du lancer » dans une bulle « de » « La liste des lancers » avec une flèche descendante égale « 6 » dans une bulle, « alors ». Ce bloc est empilé sur un bloc variable marqué « ajouter » « un » dans une bulle « à » « Nombres pairs » avec une flèche vers le bas. La séquence se termine par un bloc variable marqué « ajouter » « un » dans une bulle « à » « le numéro du lanceur » avec une flèche vers le bas, et une flèche dans le sens inverse des aiguilles d'une montre à partir du bas.
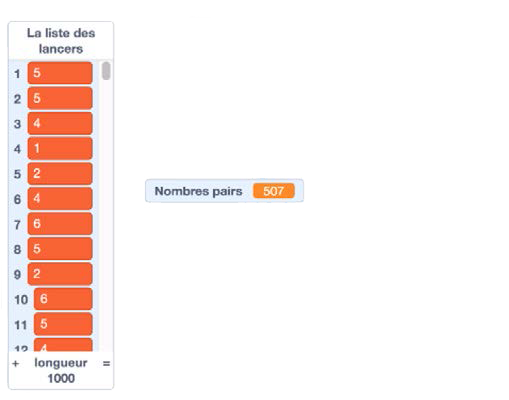
Voici le résultat généré par ce code. Le code des élèves pourrait être différent tout en demeurant fonctionnel.
| Observation possible | Pistes d’intervention |
| L’élève ne réussit pas à compiler les résultats du lancer du dé. |
Demander à l’élève de trouver le nombre de faces du dé qui lui a été remis.
|
| L’élève oublie de remettre ses variables et ses listes à zéro. |
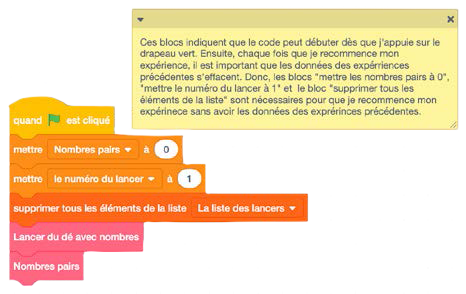 image Un bloc de texte avec une note autocollante correspondante. La note correspond à un
bloc de contrôle qui montre « quand » un drapeau vert « est cliqué ». La note autocollante correspondante se
lit comme suit : ces blocs indiquent que le code peut débuter dès que j’appuie sur le drapeau vert. Ensuite,
chaque fois que je recommence mon expérience, il est important que les données des expériences précédentes
s’effacent. Donc, les blocs « mettre les nombres pairs à zéro”, “mettre le numéro du lancer à un” et le bloc
“supprimer tous les éléments de la liste » sont nécessaires pour que je recommence mon expérience sans avoir
les données des expériences précédentes. image Un bloc de texte avec une note autocollante correspondante. La note correspond à un
bloc de contrôle qui montre « quand » un drapeau vert « est cliqué ». La note autocollante correspondante se
lit comme suit : ces blocs indiquent que le code peut débuter dès que j’appuie sur le drapeau vert. Ensuite,
chaque fois que je recommence mon expérience, il est important que les données des expériences précédentes
s’effacent. Donc, les blocs « mettre les nombres pairs à zéro”, “mettre le numéro du lancer à un” et le bloc
“supprimer tous les éléments de la liste » sont nécessaires pour que je recommence mon expérience sans avoir
les données des expériences précédentes.
Demander à l’élève de relire son code à voix haute pour voir s’il manque des consignes. Demander à l’élève d’expliquer les trois blocs identifiés. Demander à l’élève ce qui se produit lorsque les variables ne sont pas remises à zéro. Quel est l’impact sur les résultats des essais? |
| L’élève n’utilise pas correctement les blocs opérateurs. |
 image Une séquence conditionnelle, elle contient deux variables
marquées « élément » puis « le numéro du lanceur » dans une bulle « de » « La liste des lanceurs » avec une
flèche descendante égale « 2 » dans une bulle « ou », ensuite, « élément » puis « le numéro du lanceur »
dans une bulle « de » « La liste des lancers » avec une flèche descendante égale « 4 » dans une bulle « ou
», finalement, « élément » alors « le numéro du lancer » dans une bulle « de » « La liste des lancers » avec
une flèche descendante égale « 6 » dans une bulle. image Une séquence conditionnelle, elle contient deux variables
marquées « élément » puis « le numéro du lanceur » dans une bulle « de » « La liste des lanceurs » avec une
flèche descendante égale « 2 » dans une bulle « ou », ensuite, « élément » puis « le numéro du lanceur »
dans une bulle « de » « La liste des lancers » avec une flèche descendante égale « 4 » dans une bulle « ou
», finalement, « élément » alors « le numéro du lancer » dans une bulle « de » « La liste des lancers » avec
une flèche descendante égale « 6 » dans une bulle.
Demander à l’élève s’il y a une façon de faire faire davantage ce qui est voulu à l’ordinateur (utiliser le bloc « ou »). Lui faire comprendre que l’ordinateur lit une donnée à la fois, donc la virgule n’est pas utile en programmation. L’utilisation du bloc opérateur « ou » est utile pour suggérer plusieurs réponses possibles, comme 2 ou 4 ou 6 en ce qui concerne les nombres pairs. |
| L’élève répète 1 000 fois dans son code de nombre pair plutôt que de répéter la longueur de la liste. | Demander à l’élève où sont compilés les résultats des lancers de dé (les résultats des lancers de dé
devraient être compilés dans «La liste des lancers»).
Dans quelle liste dois-tu trouver les nombres pairs? Quelle variable dois-tu ajouter pour rechercher les nombres pairs? (Je dois ajouter la «longueur de la liste des lancers», de sorte que toute la liste des lancers va être répétée.)  
|
| L’élève n’utilise pas les variables adéquatement. | Demander à l’élève ce que signifient les variables. Elle ou il doit connaître la signification des variables
utilisées afin de bien comprendre son code.
image Quatre variables avec les notes autocollantes correspondantes. La première
variable est « face du dé ». La note autocollante correspondante se lit comme suit « Cette variable
représente les 6 faces d’un dé soit les nombres, « un », 2, 3, 4, 5, 6 que l’on trouve sur un dé. La
variable suivante est « La liste des lancers ». La note autocollante correspondante se lit comme suit « Une
liste est créée et on la nomme « La liste des lancers ». Cette liste compile tous les résultats dans lancers
aléatoires du dé. La variable suivante est: « « longueur de » « La liste des lancers » ainsi qu'une flèche
descendante. La note autocollante correspondante se lit comme suit: « ce bloc signifie que le programme va
passer à travers tous les résultats des lancers. Alors, le programme va revoir les mille lancers entrés dans
le tableau de « la liste des lancers ». La dernière variable est: « le numéro du lancer ». La note
autocollante correspondante se lit comme suit: « La variable “le numéro du lancer” est créée et elle
représente les cases de « un » à mille dans la liste des lancers. »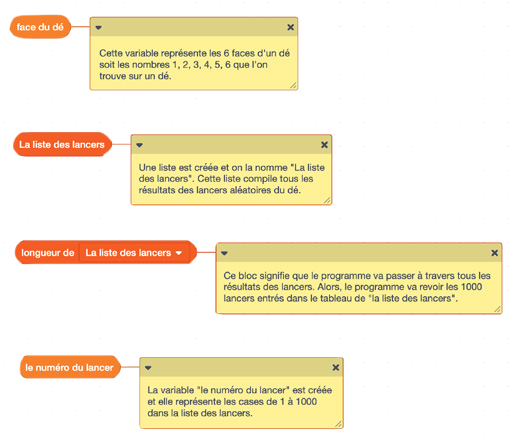
|
Note : Dans les exemples fournis, les notes en jaune sont des explications du fonctionnement du code et devraient être omises lorsque le code est présenté aux élèves.
Objectivation
Durée approximative : 15 minutes
L’évaluation peut se faire par les…

Faire un retour sur l’activité
- Quels sont les constats?
- Les résultats de la probabilité expérimentale à 20 lancers diffèrent-ils des résultats de la probabilité expérimentale à 1 000 lancers?
- Que remarquez-vous entre la probabilité théorique et la probabilité expérimentale?
- Dans votre code, quels blocs représentent des instructions conditionnelles?
- Pourriez-vous utiliser votre machine à lancers aléatoires ou une machine semblable dans d’autres situations de probabilité? Lesquelles? Pourquoi?
Consolidation
- Proposer aux élèves de modifier leur code pour vérifier la probabilité expérimentale d’obtenir un multiple de 3 ou le nombre 4.
- Proposer aux élèves de faire un code pour comparer la probabilité théorique et la probabilité expérimentale de tirer une bille rouge dans un sac de 10 billes en sachant que 3 billes sont rouges (on aborde les instructions conditionnelles si/alors/ sinon dans cet exemple).
Liens avec les autres domaines mathématiques
Nombres
B1.4 Comparer et ordonner des fractions à partir des demis jusqu’aux douzièmes, y compris des fractions impropres et des nombres fractionnaires, dans divers contextes.
B1.5 Lire, représenter, comparer et ordonner des nombres décimaux jusqu’aux centièmes, dans divers contextes. Les instructions conditionnelles (si/alors/sinon) permettent de faire des comparaisons entre des nombres en les utilisant en combinaison avec les blocs « opérateurs » (>, <, =).
Données
D2.1 Utiliser des fractions pour exprimer la probabilité que des événements se produisent, la représenter sur une ligne de probabilité et s’appuyer sur cette probabilité pour faire des prédictions et prendre des décisions éclairées.
D2.2 Déterminer et comparer les probabilités théoriques et expérimentales qu’un événement se produise. Les instructions conditionnelles permettent de coder dans des situations expérimentales avec les probabilités. La terminologie si/alors/sinon est utile pour déterminer certains événements d’une expérience aléatoire.
Littératie financière
F1.2 Estimer et calculer le coût de transactions comprenant plusieurs articles dont le prix est exprimé en dollars et en cents, en incluant les taxes de vente, à l’aide de diverses stratégies.
Avec l’élimination de la pièce de 1 cent, le coût total est arrondi au 5 cents près. En utilisant les instructions conditionnelles (si/alors/sinon), il est possible de créer des règles à suivre pour arrondir (par exemple, SI le nombre à la position des centièmes est 1 ou 2, ALORS changer la valeur à 0. SI le nombre à la position des centièmes est 3 ou 4, ALORS changer la valeur à 5, etc.).
Différenciation pédagogique et conception universelle de l’apprentissage
- Donner aux élèves les blocs débranchés pour qu’elles et ils puissent les replacer et en faire un code.
- Donner aux élèves les variables avant de commencer le code.
- Proposer un début de code pour que l’élève le termine.
- Créer certains blocs pour l’élève, comme le bloc « multiple de 3 » et le bloc « nombre pair ».
 image Un
bloc de code et une note autocollante indiquant la section correspondante. Le code commence par un bloc portant la
mention « définir » et, à côté, la mention « Nombres pairs » dans une forme ombrée légèrement plus foncée. La note
autocollante correspondante indique « On crée le bloc “Nombres pairs” pour que le code place les lancers du dé qui
donne un résultat d’un nombre pair, dans un tableau de fréquence. On ajoute donc une variable qui se nomme « Nombres
pairs » pour qu’on puisse voir la compilation des nombres pairs dans la liste des lancers aléatoires.
image Un
bloc de code et une note autocollante indiquant la section correspondante. Le code commence par un bloc portant la
mention « définir » et, à côté, la mention « Nombres pairs » dans une forme ombrée légèrement plus foncée. La note
autocollante correspondante indique « On crée le bloc “Nombres pairs” pour que le code place les lancers du dé qui
donne un résultat d’un nombre pair, dans un tableau de fréquence. On ajoute donc une variable qui se nomme « Nombres
pairs » pour qu’on puisse voir la compilation des nombres pairs dans la liste des lancers aléatoires.
Source : Guide d’enseignement efficace des mathématiques, Codage, p. 105-114.

