C2. Équations et inégalités
Démontrer sa compréhension des variables, des expressions, des égalités et des inégalités, et mettre en application cette compréhension dans divers contextes.
Situation d’apprentissage : énigmes de nombres
Durée approximative : 100 minutes
Sommaire
Dans cette situation d’apprentissage, les élèves ont recours à un raisonnement algébrique pour créer une énigme de nombres fondée sur une séquence d’opérations arithmétiques.
Intention pédagogique
Le but de cette situation d’apprentissage est d’amener les élèves :- à élaborer une séquence d’opérations arithmétiques;
- à représenter concrètement et semi concrètement une séquence d’opérations arithmétiques en mettant l’accent sur une variable;
- à utiliser la variable pour représenter un nombre dont la valeur est indéterminée;
- à raisonner algébriquement.
| Contexte pédgagogique | Préalables |
| Au cours des années d’études précédentes, les élèves ont appris à représenter des situations d’égalité et
des équations simples. À l’aide de diverses représentations, elles et ils ont aussi appris à déterminer la
valeur inconnue dans une équation simple. En 6e année, elles et ils sont aptes à représenter des
situations d’égalité dans le cadre de contextes plus complexes en utilisant des variables.
Elles et ils peuvent aussi déterminer la valeur de la variable dans une équation par inspection ou par essais systématiques. |
La présente situation d’apprentissage aide les élèves à consolider leur compréhension de la variable et à
parfaire l’utilisation des concepts algébriques à l’étude.
Pour être en mesure de réaliser cette situation d’apprentissage, les élèves doivent pouvoir représenter des équations simples de différentes façons (concrète, semi-concrète et symbolique). |
Matériel
- annexe 6.1 et annexe 6.2
- annexe 6.3 (une copie par équipe)
- feuilles grand format (une par équipe)
- jetons ou cubes
- contenants opaques (verres ou sacs)
Vocabulaire mathématique
variable, représentation, équation
Avant l’apprentissage (mise en train)
Durée approximative : 40 minutes
Animer une discussion au sujet des énigmes afin que toutes et tous les élèves en saisissent bien le sens. Enchaîner en leur expliquant que, dans la présente situation d’apprentissage, elles et ils devront chercher à comprendre, à expliquer et à créer des énigmes de nombres.
Note : Dans les énigmes de nombres ci-dessous, le nombre de départ est limité aux nombres de 1 à 10 afin de restreindre la quantité de matériel de manipulation et de dessins nécessaires aux représentations. Cette restriction facilite aussi le calcul des opérations à effectuer à chaque étape de l’énigme. Toutefois, l’énigme s’applique à tous les nombres, petits ou grands.
Proposer aux élèves l’énigme ci-dessous et leur demander d’effectuer, à l’aide d’une feuille et d’un crayon, les opérations demandées à chacune des étapes :
- Choisir un nombre naturel de 1 à 10.
- Ajouter 6 à ce nombre.
- Soustraire 3.
- Ajouter 5.
- Ajouter 2.
- Soustraire 10.
Animer un échange pour faire ressortir le fait que le résultat correspond au nombre choisi au départ en posant des questions telles que :
- Que remarquez-vous?
- Y a-t-il d’autres élèves qui ont noté cela avec d’autres nombres de départ?
- Comment peut-on expliquer cette situation?
- Y a-t-il des élèves qui n’ont pas obtenu leur nombre de départ comme résultat?
Note : Il est possible qu’au cours de la discussion certaines et certains élèves soulèvent le fait que les quantités soustraites annulent les quantités additionnées; par exemple, une ou un élève pourrait dire que, tout le long de l’énigme, on a ajouté 13 et l’on a soustrait 13.
Cette observation est très intéressante, mais il faut amener les élèves à recourir à une représentation généralisée pour montrer, à l’aide d’une variable, que l’énigme fonctionne avec tous les nombres. Un modelage aide à faire ressortir le raisonnement algébrique utilisé pour résoudre l’énigme.
Afficher l’annexe 6.1 au tableau interactif ou reproduire l’annexe 6.1 sur une feuille grand format ou sur un tableau effaçable.
Montrer aux élèves un contenant opaque dans lequel vous aurez mis un certain nombre de cubes ou de jetons (3, par exemple) sans le dévoiler aux élèves. Leur préciser que le contenant représente la variable, puisqu’il contient un nombre d’objets inconnu. Représenter ensuite les opérations demandées à chacune des étapes en utilisant des cubes ou des jetons. Effectuer les ajouts ou les retraits à côté du contenant. Au fur et à mesure, illustrer chaque étape dans la colonne Représentation à partir d’une variable.
Exemples de représentations de la première énigme de nombres :
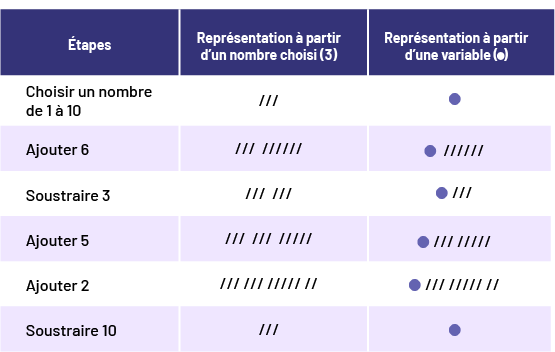 Image Tableau représentant les étapes, la représentation à partir d’un nombre choisi « 3 » et la représentation à
partir d’une variable « rond ». Choisir un nombre de, un à dix, 3 bâtons, un rond. Ajouter 6, 9 bâtons, un rond et 6 bâtons. Soustraire 3, 6 bâtons, un rond et 3 bâtons. Ajouter 5, 11 bâtons, un rond et 8 bâtons. Ajouter 2, 13 bâtons, un rond et dix bâtons. Soustraire dix, 3 bâtons, un rond.
Image Tableau représentant les étapes, la représentation à partir d’un nombre choisi « 3 » et la représentation à
partir d’une variable « rond ». Choisir un nombre de, un à dix, 3 bâtons, un rond. Ajouter 6, 9 bâtons, un rond et 6 bâtons. Soustraire 3, 6 bâtons, un rond et 3 bâtons. Ajouter 5, 11 bâtons, un rond et 8 bâtons. Ajouter 2, 13 bâtons, un rond et dix bâtons. Soustraire dix, 3 bâtons, un rond.
Modeler une deuxième fois la représentation de la première énigme de nombres, mais, cette fois-ci, en montrant le nombre d’objets dans le contenant (3 objets, par exemple). Représenter ce nombre dans la première case de la colonne Représentation à partir d’un nombre choisi (voir l’exemple précédent). Effectuer les ajouts et les retraits de manière à faire ressortir la quantité de cubes de départ. Au fur et à mesure, indiquer dans la colonne l’opération effectuée. Un tel modelage aide à établir un lien entre les deux représentations.
Présenter ensuite aux élèves la seconde énigme de nombres et leur demander d’effectuer, à l’aide d’une feuille et d’un crayon, les opérations demandées à chacune des étapes :
- Choisir un nombre naturel de 1 à 5.
- Doubler le nombre.
- Ajouter 6.
- Doubler la somme.
- Soustraire 4.
- Diviser par 4.
- Soustraire 2.
Demander ensuite aux élèves de comparer leur nombre choisi au départ avec celui obtenu à la fin. Discuter des résultats.
Grouper les élèves en équipes de deux. Remettre aux équipes des cubes ou des jetons. Projeter au TBI l’annexe 6.2. Inviter les équipes à choisir un nombre de 1 à 5 et à représenter chaque étape de la seconde énigme de nombres à l’aide des cubes ou des jetons.
Inviter ensuite une équipe à venir montrer concrètement les étapes de l’énigme. Au fur et à mesure, reproduire sur le transparent ces étapes dans la colonne Représentation à partir d’un nombre choisi (voir exemple ci-dessous).
Remplir ensuite la colonne Représentation à partir d’une variable avec les élèves (voir l’exemple ci-dessous). Discuter de l’importance de cette étape pour vérifier si l’énigme fonctionne avec n’importe quel nombre qui est représenté par la variable (concrètement par le récipient, symboliquement par le carré).
Exemples de représentations de la seconde énigme de nombres :
 Image Tableau représentant les étapes, la représentation à partir d’un nombre choisi « 2 » et la représentation à
partir d’une variable « un carré ». Choisir un nombre de, un à dix, 2 bâtons, un carré. Doubler le nombre, 4 bâtons, 2 carrés. Ajouter 6, dix bâtons, 2 carrés et 6 bâtons. Doubler la somme, 20 bâtons, 4 carrés et 12 bâtons. Soustraire 4, 16 bâtons, 4 carrés et 8 bâtons. Diviser par 4, 4 bâtons, un carré et 2 bâtons. Soustraire 2, 2 bâtons, un carré.
Image Tableau représentant les étapes, la représentation à partir d’un nombre choisi « 2 » et la représentation à
partir d’une variable « un carré ». Choisir un nombre de, un à dix, 2 bâtons, un carré. Doubler le nombre, 4 bâtons, 2 carrés. Ajouter 6, dix bâtons, 2 carrés et 6 bâtons. Doubler la somme, 20 bâtons, 4 carrés et 12 bâtons. Soustraire 4, 16 bâtons, 4 carrés et 8 bâtons. Diviser par 4, 4 bâtons, un carré et 2 bâtons. Soustraire 2, 2 bâtons, un carré.
Présenter au groupe-classe le problème de l’annexe 6.3 :
C’est à votre tour de créer une énigme de nombres dont le résultat correspond au nombre de départ. Votre énigme doit comprendre au moins six étapes, dont une impliquant la multiplication. Vous devrez la représenter à partir d’un nombre choisi et à partir de la variable.
S’assurer que la tâche à effectuer a été bien comprise en demandant à quelques élèves de l’expliquer en leurs propres mots.
Pendant l’apprentissage (exploration)
Durée approximative : 35 minutes
Grouper les élèves en équipes de deux et leur remettre une copie de l’annexe 6.3. Mettre à leur disposition des récipients opaques et du matériel de manipulation (jetons ou cubes), puis les inviter à accomplir la tâche.
Circuler parmi les équipes et soutenir les élèves dans leur travail sans toutefois leur dire comment relever le défi. Au moyen d’interventions stratégiques, les amener plutôt à réfléchir à l’utilisation d’une variable, aux stratégies à utiliser pour créer l’énigme et aux différentes formes de représentation.
Pour ce faire, leur poser des questions telles que :
- Comment pouvez-vous vous assurer que votre énigme de nombres fonctionne?
- Votre énigme fonctionnerait-elle avec tous les nombres?
Allouer suffisamment de temps aux élèves pour leur donner la chance d’explorer diverses stratégies pour créer l’énigme de nombres et en discuter.
Elles et ils peuvent :
- travailler par essais et erreurs (commencer par un nombre choisi et formuler une série d’opérations, par exemple);
- se servir de matériel de manipulation afin de représenter l’énigme et la variable;
- utiliser du matériel de manipulation avec un nombre choisi (utiliser des cubes emboîtables pour représenter le nombre choisi et effectuer une série d’opérations, par exemple);
- annuler les opérations (en multipliant par deux et en divisant par deux, par exemple).
Exemple
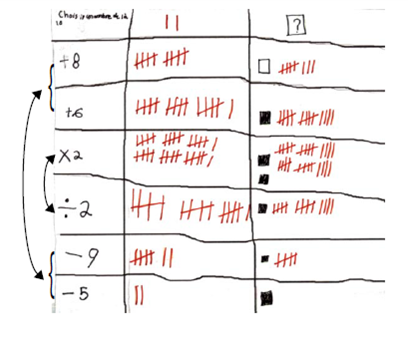 Exemple
d’tableau représentant les étapes, la représentation à partir d’un nombre choisi « 2 » et la représentation à partir
d’une variable « un carré » créé par un élève.
Exemple
d’tableau représentant les étapes, la représentation à partir d’un nombre choisi « 2 » et la représentation à partir
d’une variable « un carré » créé par un élève.
| Observation possible | Intervention possible |
|---|---|
| Certaines équipes ont du mal à créer une énigme de nombres qui fonctionne avec n’importe quel nombre. | Encourager les élèves à utiliser le matériel de manipulation pour créer l’énigme de nombres. |
| Une équipe commence par une soustraction et éprouve des difficultés à représenter cette étape avec du matériel concret lorsque le nombre de départ est inconnu. |
Leur poser des questions telles que :
|
| Une équipe commence par une division et représente cette étape en séparant la variable en parties. Toutefois, à la fin de l’énigme, l’équipe se retrouve avec une partie de la variable seulement. | Rappeler aux élèves que l’on doit arriver à la fin l’énigme avec le même symbole qu’au départ. La variable doit donc se trouver en entier. |
Demander aux élèves de noter leur énigme et leurs représentations sur une feuille grand format en vue de l’échange mathématique.

Sélectionner les équipes qui feront une présentation au moment de l’échange de façon à faire ressortir les diverses stratégies utilisées pour créer une énigme. Il est parfois utile de discuter d’une stratégie qui n’a pas donné les résultats espérés, puisque l’énigme de nombres ne fonctionne pas. Cela donne aux élèves l’occasion d’élaborer des solutions de rechange.
Après l’apprentissage (objectivation/échange mathématique)
Durée approximative : 25 minutes
Demander aux équipes sélectionnées de venir, une à la fois, expliquer leur énigme de nombres et ses représentations.
Après chaque exposé, les autres élèves enrichissent l’échange mathématique en posant des questions et en faisant des observations pertinentes dans un climat de respect.
Intervenir, au besoin, en posant aux élèves des questions telles que :
- Comment pouvez-vous vous assurer que votre énigme de nombres fonctionne?
- Peut-on essayer l’énigme avec d’autres nombres?
- Cette séquence d’opérations fonctionne-t-elle avec tous les nombres?
- Si vous deviez créer une autre énigme, que feriez-vous autrement? Que feriez-vous de semblable?
Note : Le but de cette dernière question est de faire ressortir que l’utilisation de la variable, représentée par un carré, une tasse, un sac, etc., facilite la création de l’énigme. Insister sur le fait que l’utilisation d’une variable nous assure que l’énigme fonctionne avec tous les nombres. Rappeler aux élèves qu’un symbole a le même référent tout le long d’une même situation, donc tout le long de la séquence d’opérations.
Au fur et à mesure, faire ressortir les ressemblances et les différences entre certaines énigmes de nombres. Voici quelques constatations possibles :
- Plusieurs énigmes commencent par une addition.
- Certaines équipes ont effectué une division afin d’annuler une multiplication précédente.
- Dans certaines énigmes, une étape annule une étape précédente; par exemple, + 3, et un peu plus tard, − 3.
- L’addition augmente les quantités, tandis que la soustraction les diminue.
- Dans cette énigme, on ajoute 6 en une étape (par exemple, + 6), tandis que, dans l’autre, on le fait en deux étapes (par exemple, + 2, suivi de + 4).
- Lorsqu’on effectue une multiplication, il faut l’appliquer à toute la quantité précédente.
Différenciation pédagogique
L’activité peut être modifiée pour répondre aux différents besoins
des élèves.
| Pour faciliter la tâche | Pour enrichir la tâche |
Diminuer le nombre d’étapes prescrit.
Exemple 
|
|
Suivi à la maison
À la maison, les élèves peuvent créer une énigme de nombres, la soumettre à quelques membres de leur famille pour vérifier si elle fonctionne et, par la suite, expliquer la raison pour laquelle elle fonctionne pour tous les nombres. Le lendemain, le personnel enseignant peut inviter quelques élèves à présenter leur énigme au groupe-classe et à expliquer la stratégie utilisée pour la créer.
Source : Guide d’enseignement efficace des mathématiques de la 4e à la 6e année, p. 173-183.
