C1.4 Créer et décrire des suites numériques comprenant des nombres entiers, et représenter des relations entre ces nombres.
Activité 1 : des prévisions exactes à l’aide de suites de nombres
Diviser le groupe-classe en équipes et leur donner une mise en situation. À partir de celle-ci, l’élève crée individuellement une suite de nombres représentant la situation (encourager l’élève à utiliser une table de valeurs afin d’organiser ses données). Entre elles et eux, les élèves décrivent ensuite leur règle. Chaque mise en situation devrait amener l’élève à prédire un résultat.
Marius joue avec sa calculatrice afin de trouver la réponse à des expressions.
image
Expressions suivit du résultat. Un plus (parenthèse ouvrante) moins un (parenthèse fermante) égal zéro. 2 plus
(parenthèse ouvrante) moins 2 (parenthèse fermante) égal zéro. 3 plus (parenthèse ouvrante) moins 3 (parenthèse
fermante) égal zéro. 4 plus (parenthèse ouvrante) moins 4 (parenthèse fermante) égal zéro. 5 plus (parenthèse
ouvrante) moins 5 (parenthèse fermante) égal inconnue. 6 plus (parenthèse ouvrante) moins 6 (parenthèse fermante) égal
inconnue. Etcétéra jusqu’à , 100 plus (parenthèse ouvrante) moins 100 (parenthèse fermante) égal inconnue.
- Peux-tu déduire le résultat des prochaines expressions?
- Quel serait le résultat de (500) + (-500)? Comment appelle-t-on deux nombres qui s’additionnent pour donner 0?
- Que se passe-t-il si j’inverse tous les signes, par exemple (-1) – (+ 1)?
- Fais une table de valeurs afin d’expliquer le résultat obtenu. Peux-tu prédire le résultat de (-100) – (+ 100)?
Leslie joue avec des jetons et les dispose sous la forme d’une pyramide, comme dans la figure suivante.
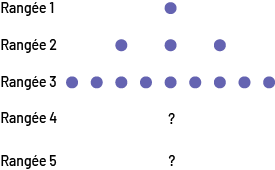Image Figure montrant des jetons placés dans la séquence de classement d'une pyramide. Rang 1 : un jeton. Rang 2 : 3 jetons. Rang 3 : 9 jetons. Rang 4 : point d'interrogation. Rang 5 : point d'interrogation.
Elle adore trouver des règles dans ses créations. De plus, elle aime les analyser afin d’élaborer des règles de correspondance et pour l’aider, elle crée une table de valeurs.
| Rangée | Nombre de jetons |
|---|---|
| 1 | 1 |
| 2 | 3 |
| 3 | 9 |
| 4 | ? |
| 5 | ? |
- Elle aimerait poursuivre sa création, mais elle n’a pas assez de jetons. Elle remarque cependant qu’il y a une régularité dans sa table de valeurs. La remarques-tu aussi? Explique ta réponse.
- Leslie veut poursuivre la réalisation de sa pyramide. Combien de jetons lui faut-il pour créer les 10 premières rangées? Est-ce réaliste?
- Combien de jetons aurait la 20e rangée? Peux-tu expliquer ta réponse à partir d’une règle de correspondance?
Activité 2 : les grains de riz (suite numérique et relation entre les nombres)
Matériel :
- échiquier;
- grain de riz;
- calculatrice.
Diviser les élèves en équipes. Leur présenter la mise en situation ci-dessous. Chaque équipe doit répondre aux questions. Faire un retour en groupe-classe afin de discuter des stratégies proposées.
Mise en situation
Antonio aime jouer avec les nombres et créer des suites. Dans sa chambre, il a un échiquier comme celui ci-dessous. Il l’utilise pour créer une nouvelle suite de nombres.
Il place des grains de riz sur les cases. Sur la case A1, il place 1 grain de riz, sur la case B1, 2 grains de riz, sur la case C1, 4 grains de riz, sur la case D1, 8 grains de riz et ainsi de suite.
Il aimerait recouvrir les 64 cases de l’échiquier.
- Combien de grains de riz y aura-t-il sur la case H1(dernière case de la première rangée)? Comment le sais-tu?
- Crois-tu qu’il pourra déposer du riz sur toutes les cases? Justifie ta réponse.
- Combien de grains de riz devra-t-il déposer sur la 64e case de l’échiquier? Décris la suite de nombres obtenue pour trouver cette réponse.
Activité 3 : la table de multiplication
Dans une table de multiplication, on trouve plusieurs régularités entre les nombres. À partir de la table ci-dessous, inviter l’élève à créer des suites de nombres. L’élève doit être en mesure de trouver des relations entre les nombres de la suite et de les décrire à ses pairs.
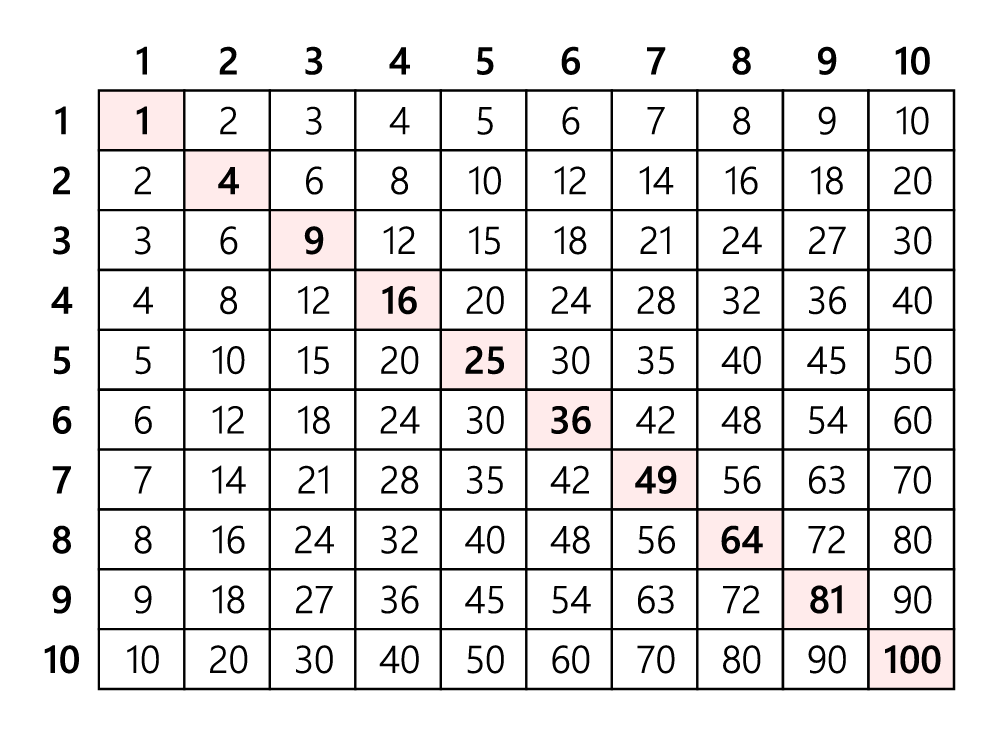
Exemples de suites possibles
Nombres pairs, nombres carrés, la suite des facteurs de 10. Amener l’élève à faire et à trouver des relations avec des suites décroissantes.
Exemples de piste de questions
- Quel type de nombres la diagonale principale représente-t-elle? Que remarques-tu à propos de la colonne et de la rangée où se situe le nombre carré en ce qui concerne sa valeur? (Par exemple, colonne 3 et rangée 3, la valeur du nombre carré est 9.)
- Que remarques-tu à propos des nombres situés dans la rangée 2 et ceux situés dans la rangée 4? Explique ta réponse.
- Comment appelle-t-on les nombres de la rangée 2?
- Les nombres de la rangée 4 ont-ils les mêmes propriétés que ceux à la rangée 2? Explique ta réponse.
- Que remarques-tu à propos des nombres situés dans la rangée 10?
Pour aller plus loin, inviter l’élève à faire des généralisations et des projections pour la table de multiplication de 20 × 20.