C2.3 Résoudre des équations qui comprennent des termes multiples, des nombres naturels et des nombres décimaux, dans divers contextes, et vérifier les solutions.
Activité 1 : stratégies pour la résolution d’équations
Quelles stratégies peut-on utiliser pour résoudre l’équation ci-dessous et trouver la valeur du m?
2m + 3 = 12
Stratégie 1
Logigramme inversé
J’utilise le logigramme inversé. Le premier logigramme illustre le déroulement des opérations appliquées à la variable pour obtenir le résultat. Le deuxième logigramme montre le déroulement des opérations inverses pour permettre de trouver la valeur de la variable.
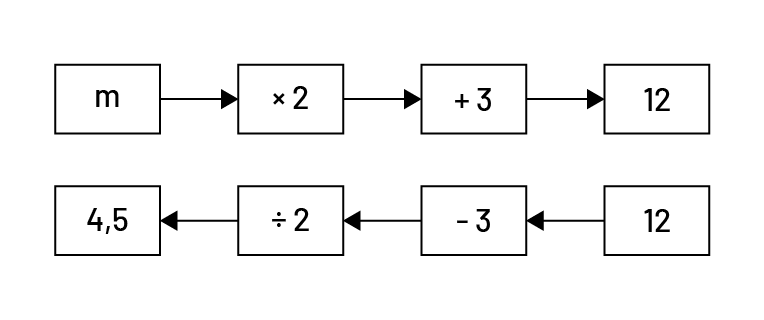
La valeur de m est 4,5.
Stratégie 2
Modèle de la balance
Lorsque j’utilise le modèle de la balance, je représente les expressions visuellement et je les manipule jusqu’à ce qu’elles soient équivalentes.
Je cherche à rassembler les valeurs inconnues et les isoler des valeurs connues. Pour isoler 2m, je dois neutraliser 3. Ce que je fais d’un côté de l’expression, je le fais aussi de l’autre. Donc, j’enlève 3 de chaque côté de l’expression.
\(\ 2m \ + \ 3 \ – \ 3 = 12 \ –\ 3\)
\(\ 2m = 9\)
Je divise ensuite chaque côté par 2 afin d’obtenir la valeur de m.
\(\frac{2}{2}m \ = \ \frac{9}{2}\)
\(m \ = 4,5 \)
La valeur de m est 4,5.
Source : En avant, les maths!, 7e année, CM, Algèbre, p. 3.
Activité 2 : résolution d’équations
Résous les problèmes ci-dessous puis vérifie tes solutions.
- \(3x + 5 = 7x - 3\)
- \(3,5k - 12 = 0,4k + 5\)
- \(-3,1f + 6.2 = 5,5f + 1.8\)
