C2.4 Résoudre des inégalités qui comprennent des termes multiples et des nombres naturels, et vérifier et présenter les solutions à l’aide de modèles et de représentations graphiques.
Habileté : résoudre des inégalités et vérifier et présenter les solutions à l’aide de modèles et de représentations graphiques
Pour faciliter l’apprentissage du concept d’inégalité, le personnel enseignant doit proposer aux élèves des activités qui les incitent à analyser des situations d’inégalité et à les traiter de manière algébrique. Il discute ensuite avec les élèves des stratégies utilisées pour analyser les inégalités en privilégiant celles qui font appel aux représentations concrètes et semi-concrètes, et qui mettent l’accent sur le sens de l’inégalité plutôt que sur l’application mécanique d’une procédure ou de calculs fastidieux.
Représenter les solutions à l’aide d’une droite numérique permet notamment aux élèves d’analyser une inégalité en misant sur leur sens du nombre, des opérations et du symbole, et de trouver l’intervalle des valeurs valides dans une situation d’inégalité.
Les élèves doivent consolider cette stratégie, puisqu’elle est à la base d’une bonne compréhension des manipulations algébriques auxquelles elles et ils seront exposés au cours des années d’études suivantes. Les élèves peuvent aussi avoir recours à ces stratégies pour résoudre des équations simples.
Source : Guide d’enseignement efficace des mathématiques, de la 4e à la 6e année, p. 200.
L’inégalité
 Description de la vidéo
Description de la vidéo
Description à venir
Représenter les solutions à l’aide d’une droite numérique
Cette stratégie consiste à lire attentivement la phrase mathématique donnée et à remplacer la variable afin de trouver l’intervalle des valeurs valides dans la situation d’inégalité. Une table de valeurs permet de trouver plusieurs valeurs pour la variable. Par la suite, la solution peut être représentée graphiquement sur une droite numérique.
Exemple
\(7y + 31 ≥ 78\)
La première colonne dans la table de valeurs représente le nombre par lequel la variable y sera remplacée dans l’expression algébrique \(7y + 31\).
La deuxième colonne dans la table de valeurs représente la solution de l’expression algébrique lorsque la variable y est remplacée par le nombre dans la première colonne.
\(7 (0) + 31\)
\(0 + 31\)
\(0 + 31 = 31\)
La troisième colonne dans la table de valeurs confirme ou réfute la validité de la valeur de la variable y.
Est-ce que \(31 ≥ 78\)? La réponse est non.
| y | 7y + 31 | ≥78 |
|---|---|---|
| 0 | 31 | non |
| 1 | 38 | non |
| 2 | 45 | non |
| 3 | 52 | non |
| 4 | 59 | non |
| 5 | 66 | non |
| 6 | 73 | non |
| 7 | 80 | oui |
| 8 | 87 | oui |
| 9 | 94 | oui |
| 10 | 101 | oui |
L’intervalle des valeurs valides peut être représenté à l’aide d’une droite numérique :
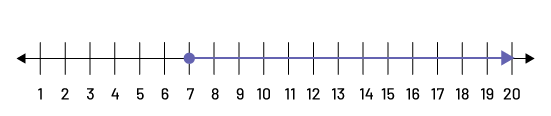
La solution est donc \(y ≥ 7\).
Note : Sur une droite numérique, un point vide indique une relation d’inégalité stricte (« est inférieur à » ou « est supérieur à »); un point plein indique une relation d’inégalité large (« est inférieur ou égal à » ou « est supérieur ou égal à »).
Une fois que l’élève a résolu une inéquation, vérifier sa solution en insérant cette valeur dans l’inéquation initiale est une excellente habitude à prendre.
La résolution d’inéquations : isoler la variable et représenter l’ensemble-solution sur une droite numérique.
 Description de la vidéo
Description de la vidéo
Description à venir
Exemple
Lorsque l’on résout l’inéquation \(5m - 4 < 2 m + 8\), il est préférable de regrouper les termes semblables ayant une variable sur le côté où le coefficient est le plus élevé (le plus positif), dans ce cas-ci à gauche.
On obtient \(m < 4\).

Pour vérifier si la solution est vraie, on peut remplacer la valeur de m par des valeurs autour de 4, par exemple 3, 4 et 5.
\(\displaylines{\begin{align} 5(3) - 4 &< 2 (3) + 8 \\ 15 - 4 &< 6 + 8 \\ 11 &< 14 \end{align}}\)
C’est vrai.
\(\displaylines{\begin{align} 5(4) - 4 &< 2(4) + 8 \\ 20 - 4 &< 8 + 8 \\ 16 &< 16 \end{align}}\)
Cette inégalité est fausse.
\(\displaylines{\begin{align} 5(5) - 4 &< 2(5) + 8 \\ 25 - 4 &< 10 + 8 \\ 21 &< 18 \end{align}}\)
Cette inégalité est fausse.
Connaissance : inégalité
Relation d’ordre entre deux expressions ou deux quantités. Il existe quatre symboles d’inégalité :
<, qui signifie « strictement inférieur à/plus petit que »;
>, qui signifie « strictement supérieur à/plus grand que »;
≤, qui signifie « inférieur ou égal à »;
≥, qui signifie « supérieur ou égal à ».
Non-égalité
Relation entre deux expressions ou deux quantités qui n’ont pas la même valeur.
La non-égalité est représentée par le signe « ≠ » (n’est pas égal à, n’égale pas).
Exemple
\(\displaylines{\begin{align} 5 &≠ 5 +1 \\ (3 \times 5) + 4 &≠ 3 \times (5 + 4) \\ 8a &≠ 25 \end{align}}\)
Source : Guide d’enseignement efficace des mathématiques, de la 4e à la 6e année, p. 70.
