C1.3 Déterminer et utiliser les règles pour prolonger des suites, faire et justifier des prédictions et trouver les termes manquants dans des suites croissantes et des suites décroissantes comprenant des nombres rationnels, et utiliser les représentations symboliques des règles pour trouver des valeurs inconnues dans des suites croissantes et décroissantes linéaires.
Activité 1 : trouvons des régularités (suites croissantes et décroissantes)
Diviser le groupe-classe en équipes. Leur donner une mise en situation. À partir de celle-ci, individuellement, elles et ils créent une suite de nombres représentant la situation (encourager les élèves à utiliser une table de valeurs afin d’organiser leurs données). Par la suite, entre eux, les élèves décrivent leur règle de régularité. Chaque mise en situation devrait amener l’élève à se questionner sur le type de suite retrouvé et par la suite, sur les différentes propriétés retrouvées.
Exemples de mise en situation
Exemple 1 : Sophia souscrit un abonnement à un centre de conditionnement physique. Elle doit payer des frais d’inscription de 35 $. Par ailleurs, les frais mensuels sont de 45,50 $.
- Créez une table de valeurs qui représente la relation entre les frais à payer et le nombre de mois pour une année.
- De quel type de suite s’agit-il? Justifiez votre réponse.
- Quelle est la valeur initiale et quel est le taux constant dans cette suite?
- Utilisez une équation pour répondre à la question suivante : avec 490 $, combien de mois d’abonnement peut-elle payer?
Source : En avant, les maths!, 8e année, CM, Algèbre, p. 4.
Exemple 2 : Pour la suite à motif répété suivante, créez une table de valeurs afin de représenter la relation entre le rang de la figure et la valeur du terme (nombre de carrés).
- Utilisez une équation pour déterminer le rang de la figure qui aura 99 carrés.
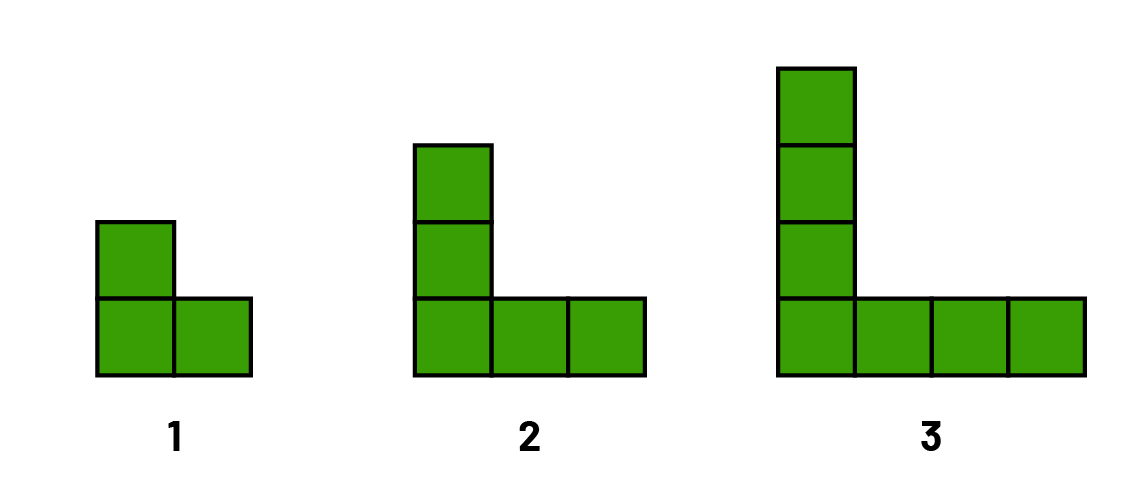
Source : En avant, les maths!, 8e année, CM, Algèbre, p. 6.
Exemple 3 : Une compagnie de plomberie offre ses services pour effectuer des travaux à domicile à un coût de 80 dollars de l’heure, plus des frais de 100 dollars pour l’appel de service.
- Créez une table de valeurs qui représente la relation entre le montant total de la facture et le nombre d’heures nécessaires pour effectuer les travaux.
- De quel type de suite s’agit-il? Justifiez votre réponse.
- Quelle est la valeur initiale et quel est le taux constant dans cette suite?
- À combien s’élèvera la facture si cinq heures sont nécessaires pour effectuer les travaux?
- Utilisez une équation pour déterminer le nombre d’heures nécessaires pour effectuer les travaux si le coût de la facture s’élève à 380 $.
Activité 2 : le carrousel des suites
Diviser le groupe-classe en équipes. Présenter des fiches différentes à chaque équipe sous la forme de stations (environ 10 minutes par station; faire une rotation). Chaque fiche contient une mise en situation, une table de valeurs ou une représentation graphique. Les membres doivent répondre à une série de questions à chaque station pendant le temps alloué. Circuler et noter les différentes stratégies des élèves. Faire participer les équipes dans le retour.
Exemples de stations dans le carrousel
Station 1
La table de valeurs suivante représente le nombre de colliers fabriqués par Jalal durant son quart de travail :
| Nombre d’heures (h) | 2 | 4 | 6 | 8 |
|---|---|---|---|---|
| Nombre de colliers fabriqués (n) | 1,5 | 3 | 4,5 |
- Déterminez le nombre de colliers qu’il réussit à fabriquer en trois heures.
- Déterminez le nombre de colliers qu’il réussit à fabriquer en huit heures.
- S’il travaillait 12 heures, combien de colliers serait-il capable de fabriquer?
- Quelle équation représente le nombre de colliers fabriqués par Jalal?
Station 2
La température maximale diminue de 0,75 degrés chaque jour depuis une semaine. S’il faisait 23 degrés il y a une semaine,
- Écrivez une équation représentant la variation de la température dans la dernière semaine. Expliquez ce que signifie le taux de variation dans cette situation.
- Si cette diminution constante se poursuit, quelle devrait être la température après cinq jours?
- Placez les données dans une table de valeurs et trouvez la température d’aujourd’hui.
- Expliquez comment obtenir le terme au rang 8 dans cette situation.
Station 3
Le tableau suivant représente le coût total pour avoir un cellulaire et l’utiliser. Les frais d’utilisation sont facturés mensuellement.
| Nombre de mois d’utilisation (n) | 0 | 2 | 5 | 10 |
|---|---|---|---|---|
| Coût total (c) | 500 | 575,40 | 688,50 | 877 |
- Selon vous, pourquoi y a-t-il un coût de 500 $ au départ?
- Déterminez le coût total après 1 mois d’utilisation.
- Déterminez la règle qui définit cette situation et représentez-la à l’aide d’une équation.
- Quel sera le coût total après 1 an d’utilisation?
