C1.2 Create and translate patterns using various representations, including shapes and numbers.
Skill: Representing Patterns in Different Ways
Non-Numeric Patterns with Repeating Elements
Using multiple representations of the same pattern can support students in deepening their understanding. Non-numeric patterns with repeating elements can be represented using concrete or visual (semi-concrete) materials, symbols, and verbal descriptions.
Examples of Representation Modes
| Representation Modes | Examples |
|---|---|
| Concrete Material | Patterns made with: the body, such as sounds, movements or positions, or objects, such as necklaces
Pattern A 
Pattern B 
|
| Visual Material (Semi-Concrete) |
Illustrated Pattern Pattern C 
|
| Oral Descriptions | Pattern A: "This is a pattern because the positions standing with arms outstretched and
squatting are always repeated in the same order Pattern B: "The necklace makes a pattern because the four colours always repeat the same over and over." Pattern C: "It's a pattern because the pattern core of a fire truck followed by a firefighter always repeats in that order." |
| Symbols | Pattern A: The structure of the pattern is AB. Pattern B: The structure of the pattern is ABCD. Pattern C: The structure of the pattern is AB. |
To translate the representation of a pattern from one form to another involves maintaining the order of the repeating elements or the repeating operation from one position to the next.

Change can also occur within the same mode of representation.
Example


By representing a pattern with symbols, it is possible to clearly identify its structure. To do this, letters are used in alphabetical order. Each new letter represents a different element in the pattern. In the patterns shown above, the structure is AABB.
Often, multiple representations of the same patterns are a good mathematical justification, as each contributes to the understanding of the ideas presented. The ability to create, interpret, and represent ideas in multiple ways is a powerful tool.
Source: translated from Guide d’enseignement efficace des mathématiques de la maternelle à la 3e année, Modélisation et algèbre, Fascicule 1, Régularités et relations, p. 34-36.
Pattern with Repeating Operation
Patterns with repeating operations can be represented using concrete or visual (semi-concrete) materials, symbols, or verbal descriptions.
| Representation Modes | Examples |
|---|---|
| Concrete Material |
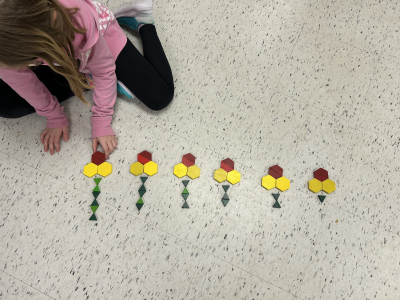
|
| Visual Material Semi-Concrete |
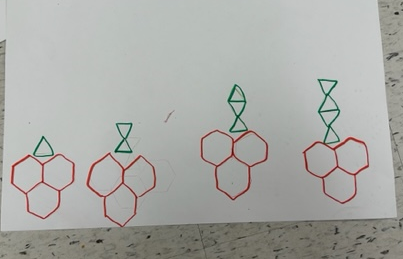
|
| Oral Description | "A trunk is always added to the trunk of the tree in the previous row." |
| Symbols | In the drawing above, the repeat operation can be represented symbolically using the operation sign (e.g., addition signs) with its corresponding value (for example, + 1). |
Symbols
Students use symbols to communicate the repeat operation. These symbols can be numbers with an understanding of the operation or an operation symbol such as addition symbols.
Source: translated from Guide d’enseignement efficace des mathématiques de la maternelle à la 3e année, Modélisation et algèbre, Fascicule 1, Régularités et relations, p. 41-42.
Students should have the opportunity to explore and create different representations of the same pattern. For example, students can be asked to exchange their representation and reproduce the pattern using concrete or visual (semi-concrete) materials, and vice versa. It is important to focus on the relationship between the two representations so that the focus remains on reasoning and not on numerical calculation.
Number Patterns
The acquisition of concepts related to number patterns is a prerequisite to the study of more abstract algebraic concepts. The exploration of various representations of number patterns facilitates the entry into the world of algebra.
In the primary grades, certain representations facilitate the development of problem-solving, reasoning, and communication skills. The representations of number patterns explored in the Primary Division are made using concrete or visual (semi-concrete) materials (hundred chart, number pocket, number line, number grid), symbols, and oral descriptions.
Examples of Representation Modes
| Representation Modes | Examples |
|---|---|
| Concrete Material |
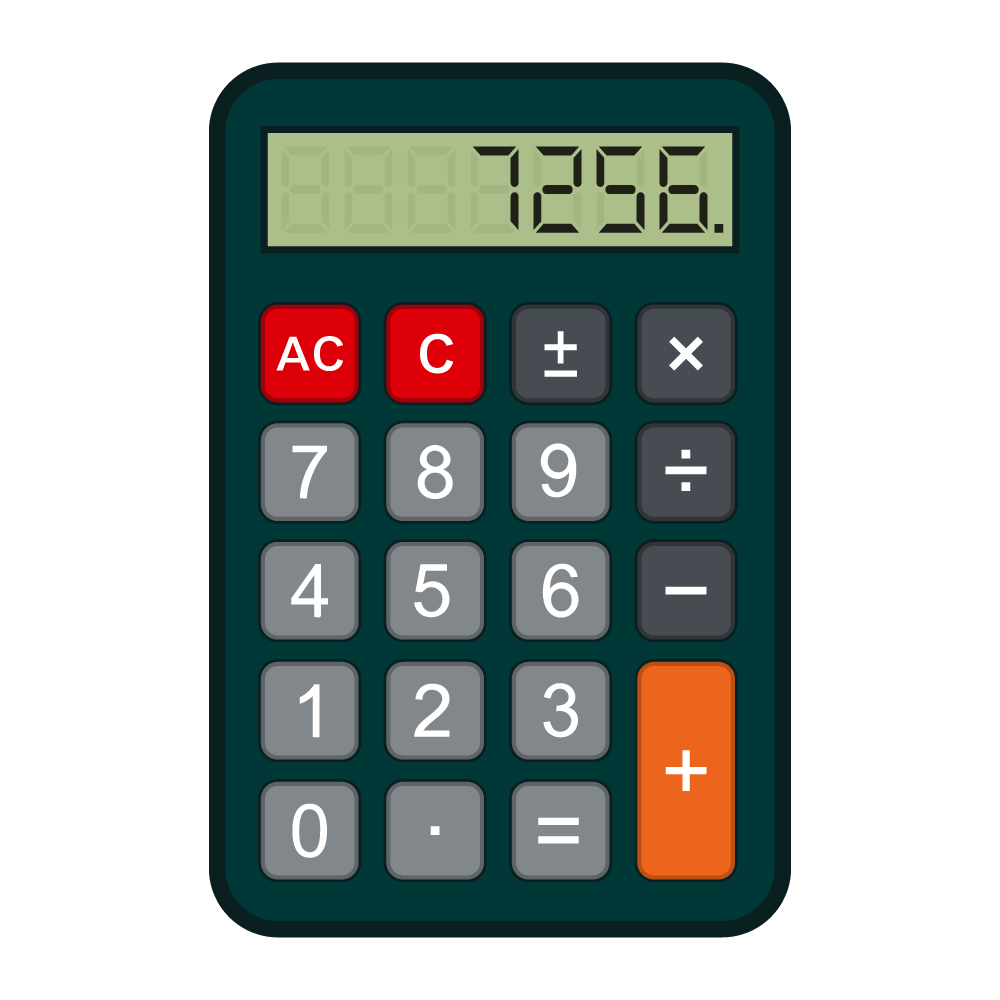 
|
| Visual Material Semi-Concrete |
|
| Verbal Description |
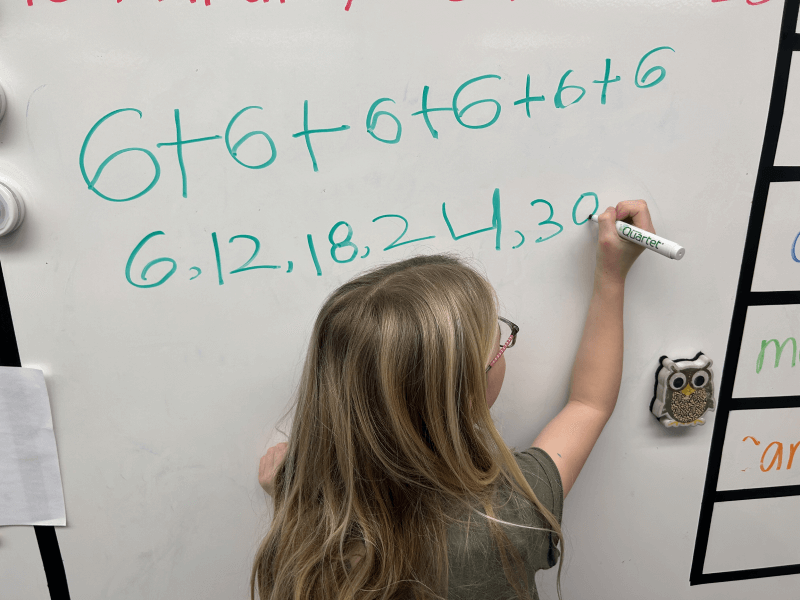
"The number pattern is: 6 vegetables the 1st week, 12 vegetables the 2nd week, 18 vegetables the 3rd week, 24 vegetables the 4th week and 30 vegetables the 5th week. The pattern rule is my vegetable garden always produces 6 more vegetables than the previous week." |
| Symbols | In the previous example, the pattern rule in the number pattern is represented by the sign + and the number 6, that is + 6. |
Representations of number patterns are made using a variety of concrete and visual (semi-concrete) materials. In the following, the types of manipulatives listed below will be used as models to further the understanding of number patterns:
- number pocket charts;
- number grid (e.g, hundred chart);
- number line;
- calculator.
Number Pocket Charts
There are many pattern rules related to a number pocket chart, and to how the patterns are displayed. In an array of 100, for example, such as the one shown below, a pattern with the pattern rule +2 will be arranged in a row (for example, 61, 63, 65…); if the pattern rule is +10, the pattern will be displayed in a column (for example, 7, 17, 27…); if the pattern rule is +11, it will be displayed in a slanting line (for example, 1, 12, 23…). In a number pocket chart, number cards can easily be moved, rotated, or removed to create patterns.

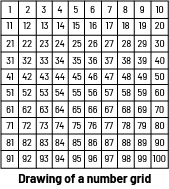
Number Grid
Here are some possible strategies for exploring number patterns with hundred grid:
- Use bingo chips to record a pattern on a grid of 100. Using tokens allows students to make changes without having to erase.
Example 1

- Use a masking card and move it around the grid to highlight a number pattern. Determine the pattern rule in this pattern and extend it.
Example 2
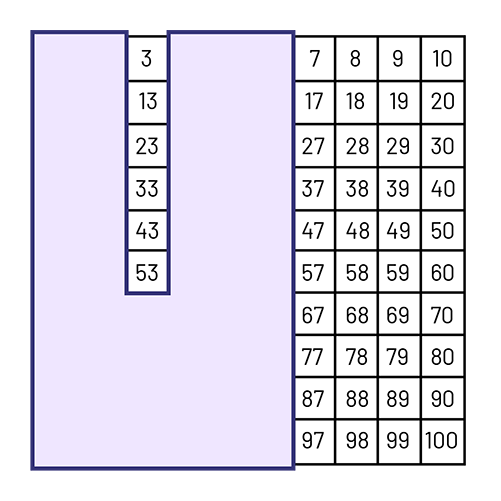
Pattern: 3, 13, 23, 33, 43, 53, 63, 73, 83, 93
Pattern Rule: +10
- Introduce sections of the grid and identify a number pattern. Determine the pattern rule in this pattern.
Example 3
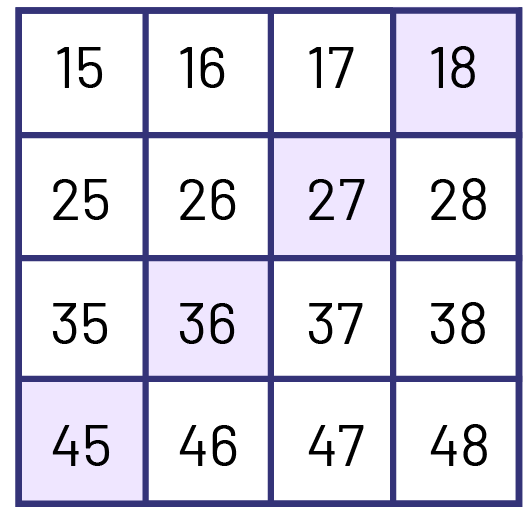
Pattern: 18, 27, 36, 45
Pattern Rule: +9
When exploring number patterns on a 100 grid, ask questions to develop the ability to represent them. For example:
- What do you notice about the numbers in the following?
- What change is there from one number to another in each row or column? (They increase or decrease by 1 or 10.)
- If the numbers were listed only in the first three rows, how would you determine which box contains the number 65?
- Where would the number 105 be if the grid was extended? How do you know?
- If the masking card is moved and the first number is 5, will the number 46 appear? Explain your answer.
Number Line

Used as a model for discovering pattern rules in patterns, the number line helps to represent a variety of patterns. The representation of the number line can be concrete or visual (semi-concrete).
Here are some possible strategies for exploring number patterns using a number line:
- Initially, use a laminated number line on which the pupils can make jumps across the numbers, at regular intervals, by jumping with their fingers or by using any object.
- Using a number line drawn on a large sheet of paper, students circle the terms in the pattern and indicate, with arrows, the pattern rule in the pattern.

As students explore number patterns using a number line, ask questions such as:
- Would the number 58 be part of the pattern if the number line were extended?
- What do you notice about the circled numbers on the number line?
- What is the pattern rule in the following? How is it indicated?
- If the pattern started with the number 1, what would be the same? different?
- If the pattern started with the number 2, what would be the same? different?
Calculator
The calculator is an electronic tool that allows students to explore numerical regularities and easily extend patterns using the function Constant Factor. Before doing so, it is important to model data entry using a virtual calculator.
Example 1
Choose a starting number between 0 and 9. Then add a number to that number continuously; for example:
- press the numeric key [7];
- add an interval of 4 by pressing the [+] key, then the numeric key [4];
- press the [=] key repeatedly;
- write, as you go along, the corresponding number pattern on a sheet of paper (in this case: 7, 11, 15, 19, 23…);
- Indicate the pattern rule in the following (+4).
Ask students thought-provoking questions such as:
- Which numbers always appear in the units position? What changes when the starting number or interval is changed?
- How many terms does the pattern contain before a unit digit repeats?
- Do you think that by counting by 4, the number 37 will be displayed? How do you know that?
Example 2
Create, as in example 1, a pattern whose starting number is 23 and whose pattern rule is +12 (23, 35, 47, 59, 71…).
Ask students questions such as:
- Is there a pattern rule in this pattern? What is it?
- If the pattern were extended indefinitely, would the number 155 be part of the pattern? What do you need to do to find out?
Example 3
Create, as in the previous examples, a pattern whose starting number is 11 and whose pattern rule is +11 (11, 22, 33, 44, 55…).
Ask students questions such as:
- If the pattern is extended, what will be the term in the 7th term? The term in the 18th term?
- Will the number 198 be part of this pattern?
Source: translated from Guide d’enseignement efficace des mathématiques de la maternelle à la 3e année, Modélisation et algèbre, Fascicule 1, Régularités et relations, p. 58-59.
Skill: Creating Various Patterns
Before creating patterns, students must first recognize, compare, describe, change the representation, and extend a wide variety of patterns.
Students demonstrate their understanding of the concept of a relationship or rule by creating a pattern and explaining it.
Initially, the use of manipulatives is essential for representing patterns, because when constructing patterns, students can more easily change one element of the pattern and check the rule. However, by drawing the pattern on paper, students focus more on the pattern to be reproduced rather than examining the entire pattern and thinking about the nature of the pattern.
Initially, teachers have students work in small groups to encourage the exchange of ideas. They can provide them with the attributes and structure of the pattern, as well as the materials required to create it.
During a mathematical discussion (consolidation/debrief), presentations of the patterns help to identify different representations of the same rule and to check how students communicate their understanding.
Next, students can be asked to create a pattern and exchange it with someone else. Students can then construct a different representation of the received pattern, describe its structure, extend it or produce a completely different one for comparison. The number of elements in the pattern should be limited, however, as some students use too many, making it difficult to identify the structure of the pattern.
Here are some examples of activities for creating number patterns:
Example 1
Provide a pattern rule for addition or subtraction (for example, +3 or -3). Have students create different patterns with this pattern rule and compare them.
Example 2
On a hundreds chart, ask students to create two patterns in which the numbers 6, 12, 24, 42, and 54 are found and whose addition pattern rule is other than +1.
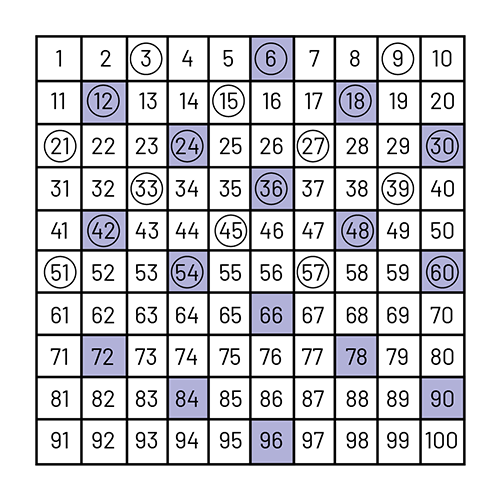
Note: The possible patterns which meet the two stated criteria are the patterns whose rule is +2, +3 or +6.
Example 3
Ask students to create two different number patterns in which the numbers 33 and 57 are found and whose addition pattern rule is other than +1.

Solution: The possible pattern rules for creating patterns that meet the stated criteria are +2, +3, +4, +6, +8, +12 and +24.
Note: It is important for students to leave a record of their process for reference during the consolidation. For example, they can:
- circle the terms of each pattern;
- draw an arrow above each jump to indicate the interval;
- symbolically represent the pattern rule with a + sign, as in the example below.
Possible Solution

Source: translated from Guide d’enseignement efficace des mathématiques de la maternelle à la 3e année, Modélisation et algèbre, Fascicule 1, Régularités et relations, p. 39-40 et 63-65.
Skill: Making Connections Between Different Representations
A mathematical relationship is a connection that exists in a particular context between objects, ideas, or numbers.
Source: translated from Guide d’enseignement efficace des mathématiques de la maternelle à la 3e année, Modélisation et algèbre, Fascicule 1, Régularités et relations, p. 18.
Mathematical models are used to study relationships. Over time, mathematicians have created, used, and generalized certain ideas, strategies, and representations to make concepts easier to grasp. Through use, certain representations have become accepted models, for example, the number line and the ten-frame. It is important that students use mathematical models in a variety of activities to understand relationships between quantities.
When faced with a problem situation, several representations are possible; some students use their bodies, manipulatives or drawings, while others represent the data more schematically. The way in which data is appropriated and organized using models reflects the level of development of algebraic thinking. The models explored in the primary and junior grades will differ depending on the students' level of abstraction. The ten frame, the array, the table of values, the open number line, and the double open number line are models to be encouraged in the primary grades.
It is important to use these models and to teach students to use them to help them reason. In representing a problem situation, students analyze relationships using models, draw conclusions, and explain them using oral descriptions. Models are tools that help them formalize their algebraic thinking.
Models applied to multiple contexts promote analysis and introduce students to a level of abstraction that facilitates predictions and generalizations. Dialogue, mathematical discussions about the problem data represented with different models, and questions from teachers provoke student reflection.
Source: translated from Guide d’enseignement efficace des mathématiques de la maternelle à la 3e année, Modélisation et algèbre, Fascicule 1, Régularités et relations, p. 18-21.
Comparing patterns provides a better understanding of their characteristics, promotes reflection, facilitates communication, and allows students to develop their algebraic reasoning.
Source: translated from Guide d’enseignement efficace des mathématiques de la maternelle à la 3e année, Modélisation et algèbre, Fascicule 1, Régularités et relations, p. 59.
Non-Numeric Repeating Patterns
Observing similarities and differences between certain patterns reinforces students' learning and develops their communication skills.
When discussing mathematics, students should be led to compare the special characteristics of patterns, such as:
- the attributes;
- the choice and quantity of elements in each pattern;
- the structure of each pattern;
- the pattern rule.
Examples
| Pattern 1 | Pattern 2 |
|---|---|

|
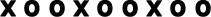
|
| Attributes: shape and colour | Attribute: symbols |
| 3 elements pattern: 1 yellow circle and 2 blue trapezoids | 3 elements pattern: one x symbol and two o symbols |
| Structure: ABB | Structure: ABB |
| Pattern rule: a yellow circle followed by two blue trapezoids, always in the same order. | Pattern rule: the x symbol followed by two o symbols, always in the same order. |
The ability to compare patterns facilitates the development of the ability to extend patterns and, subsequently, to create new ones. To get students to create a mental image of a rule, teachers can also have students compare patterns using examples and counterexamples of patterns. This strategy allows students to recognize a pattern, identify the pattern core, describe it and justify their reasoning while using appropriate mathematical vocabulary.
Example of a pattern with a repeating pattern core:

Non-Example of a Pattern - No Pattern Core:

Source: translated from Guide d’enseignement efficace des mathématiques de la maternelle à la 3e année, Modélisation et algèbre, Fascicule 1, Régularités et relations, p. 33-34.
Patterns with a Repeating Operation
The approaches described above for comparing non-numeric repeating patterns also apply to patterns with a repeating operation.
Source: translated from Guide d’enseignement efficace des mathématiques de la maternelle à la 3e année, Modélisation et algèbre, Fascicule 1, Régularités et relations, p. 40.
