C1.2 Créer des suites à l’aide d’une variété de représentations, y compris des nombres et des formes géométriques, et établir des liens entre les différentes représentations.
Habileté : représenter les suites de différentes façons
Suites non numériques à motif répété
L’utilisation de représentations multiples d’une même suite pour communiquer sa compréhension est une composante essentielle du développement de la pensée algébrique. Les suites à motif répété peuvent être représentées à l’aide de matériel concret ou semi-concret, de symboles ou de descriptions orales.
Exemples de modes de représentation
| Modes de représentation | Exemples |
|---|---|
| Matériel concret | Suites faites avec :
|
| Matériel semi-concret | Suite Illustrée
|
| Descriptions orales | Suite A : « C'est une suite parce que les positions debout bras tendus et
accroupie se répètent toujours dans le même ordre. » Suite B : « Le collier fait une suite parce que les quatre couleurs se répètent toujours pareil encore et encore. » Suite C : « C'est une suite parce que le motif un camion d'incendie suivi d'un pompier se répète toujours dans cet ordre. » |
| Symboles | Suite A : La structure de la suite est AB. Suite B : La structure de la suite est ABCD. Suite C : La structure de la suite est AB. |
Les élèves peuvent démontrer leur compréhension des concepts de régularité et de relations, et développer davantage leurs habiletés à reconnaître, à décrire et à prolonger une suite en changeant la représentation d’une suite sans en modifier la règle. Le changement peut se faire d’un mode à un autre. Par exemple, une suite non numérique telle que celle illustrée ci-dessous peut être représentée avec les mouvements « tape, saute, saute » ou avec de petits animaux en plastique « chat, chien, chien ».
Le changement peut aussi se faire à l’intérieur d’un même mode de représentation.
Exemple
En représentant une suite à l’aide de symboles, il est possible d’identifier clairement sa structure. Pour ce faire, des lettres sont utilisées selon l’ordre alphabétique. Chaque nouvelle lettre représente un élément différent dans le motif. Dans les suites présentées ci-dessus, la structure est AABB.
Plusieurs représentations d’une même suite constituent souvent une bonne justification mathématique, puisque chacune d’elles contribue à la compréhension des idées présentées. L’habileté à créer, à interpréter et à représenter de plusieurs façons ses idées est un outil puissant.
Source : Guide d’enseignement efficace des mathématiques de la maternelle à la 3e année, p. 34-36.
Suites non numériques à motif croissant
L’utilisation de représentations multiples d’une même suite pour communiquer sa compréhension est une composante essentielle du développement de la pensée algébrique. Les suites non numériques à motif croissant, tout comme les suites à motif répété, peuvent être représentées à l’aide de matériel concret ou semi-concret, de symboles ou de descriptions orales.
| Modes de représentation | Exemples |
|---|---|
| Matériel concret |
|
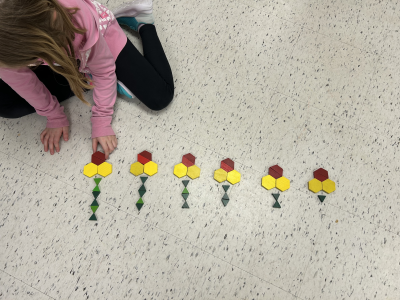
| Matériel semi-concret |
|
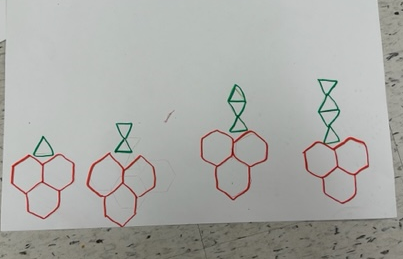
| Description orale | "Un tronc est toujours ajouté au tronc de l'arbre du rang précédent." |
| Symboles | Dans le dessin ci-dessus, la règle de la suite des figures peut être représentée symboliquement par le signe d'addition et le nombre (+1). |
Symboles
Les élèves peuvent utiliser des symboles pour laisser des traces qui montrent leur compréhension de la règle dans une suite non numérique à motif croissant. Ces symboles peuvent être des nombres ou des symboles d’addition.
Source : Guide d’enseignement efficace des mathématiques de la maternelle à la 3e année, p. 41-42.
Les élèves doivent avoir l’occasion d’explorer et de créer diverses représentations d’une même suite. À titre d’exemple, il est possible de leur demander de s’échanger leur représentation et d’en reproduire la suite à l’aide de matériel concret ou semi-concret, et vice versa. Il est important de s’attarder à la relation entre les deux représentations pour que l’accent demeure sur le raisonnement et non sur le calcul numérique.
Suites numériques
L’acquisition des concepts relatifs aux suites numériques est un préalable à l’étude des concepts algébriques plus abstraits. L’exploration de diverses représentations de suites numériques facilite l’entrée dans le monde algébrique.
Au cycle primaire, certaines représentations facilitent le développement des habiletés en résolution de problèmes, en raisonnement et en communication. Les représentations des suites numériques explorées au cycle primaire sont réalisées à l’aide de matériel concret ou semi-concret (tableau de nombres, droite numérique, grille de nombres), de symboles et de descriptions orales.
Exemples de modes de représentation
| Modes de représentation | Exemples |
|---|---|
| Matériel concret |
 
|
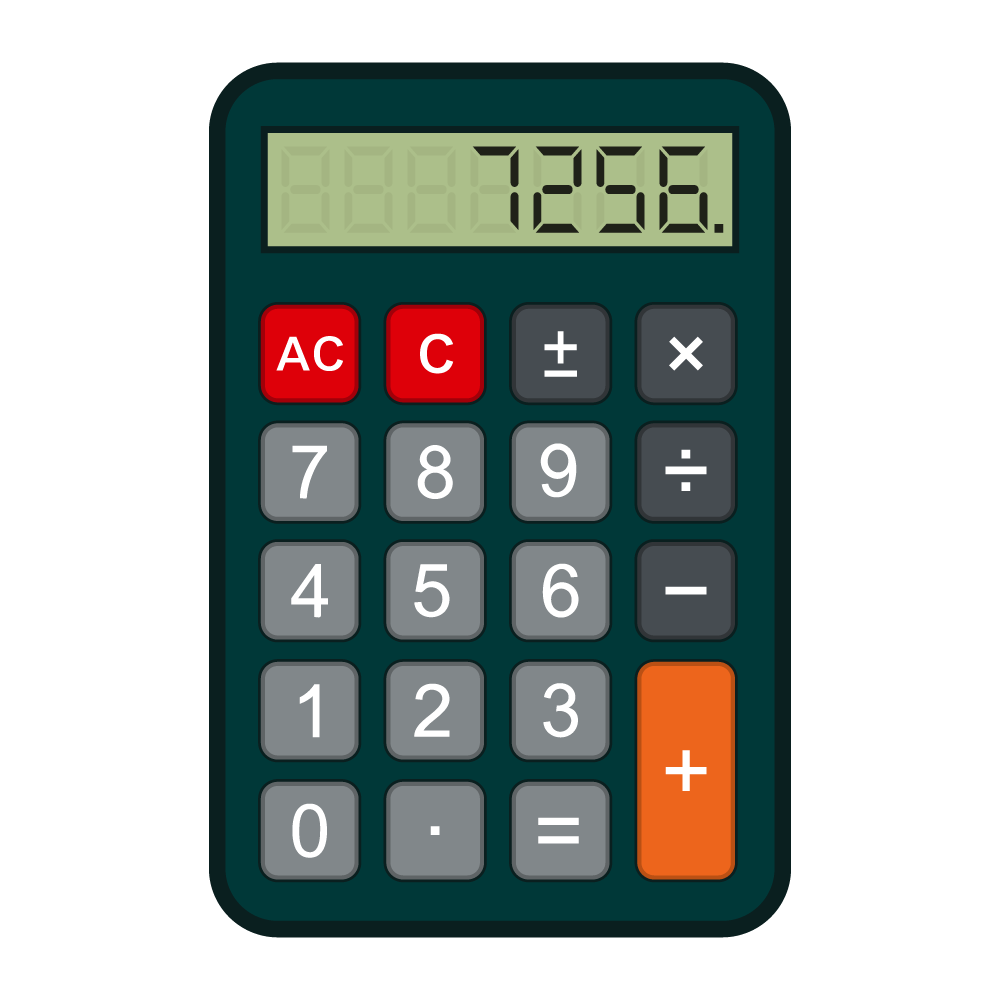
| Matériel semi-concret |
 
|
| Description orale |
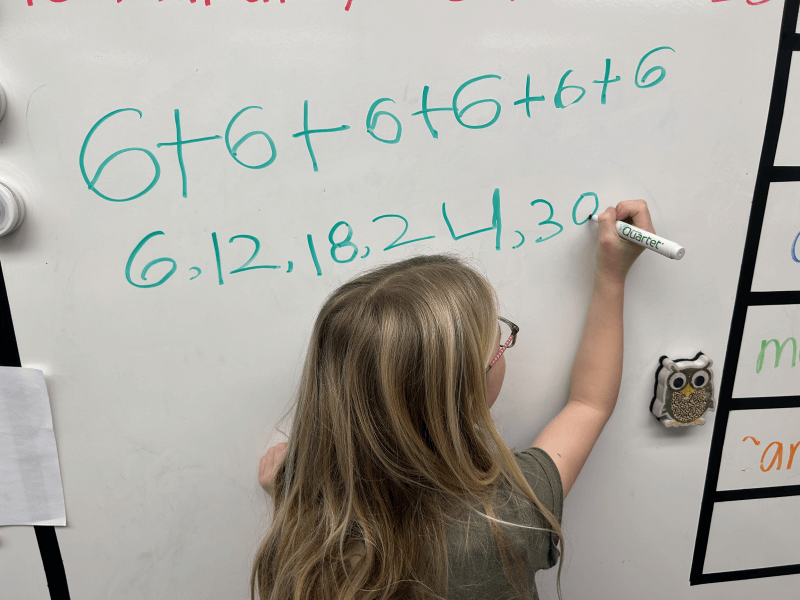
« La suite numérique est : 6 légumes la 1re semaine, 12 légumes la 2e semaine, 18 légumes la 3e semaine, 24 légumes la 4e semaine et 30 légumes la 5e semaine. La règle de régularité que présente mon potager est toujours 6 légumes de plus que la semaine précédente. » |
| Symboles | Dans l'exemple précédent, la règle de régularité dans la suite numérique est représentée par le signe + et le nombre 6, soit +6. |
Les représentations de suites numériques se font à l’aide de divers matériels concrets et semi-concrets. Dans ce qui suit, le matériel de manipulation énuméré sera utilisé comme modèle pour approfondir la compréhension des suites numériques :
- le tableau de nombres;
- la grille de nombres;
- la droite numérique;
- la calculatrice.
Tableau de nombres
Les régularités, dans un tableau de nombres, sont multiples de même que la disposition des suites. Dans un tableau de 100, par exemple, tel que celui illustré ci-dessous, une suite ayant la régularité +2 sera disposée en rangée (par exemple, 61, 63, 65…); si la régularité est +10, la suite sera disposée en colonne (par exemple, 7, 17, 27…); si la régularité est +11, elle sera disposée en droite oblique (par exemple, 1, 12, 23…). Dans un tableau de nombres, les cartes de nombre peuvent facilement être déplacées, tournées ou enlevées pour créer des suites.
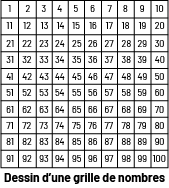
Grille de nombres
Voici quelques stratégies possibles pour explorer les suites numériques à l’aide d’une grille de nombres de 100 :
- Utiliser des jetons de bingo pour identifier une suite sur une grille de 100. L’utilisation de jetons permet aux élèves de faire des modifications sans avoir à effacer.
Exemple
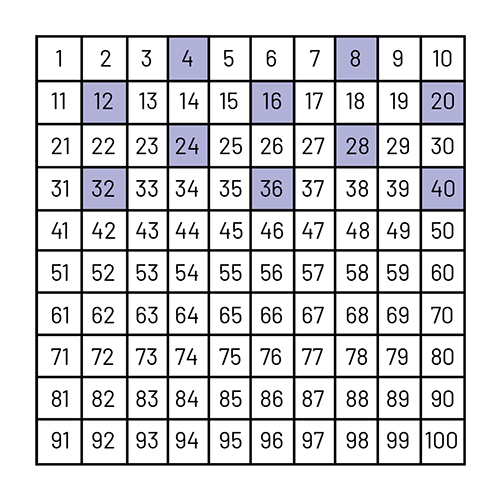
Suite: 4, 8, 12, 16, 20, 24, 28, 32, 36, 40
Règle de régularité : + 4
- Utiliser un pochoir et le déplacer sur la grille pour repérer une suite numérique. Identifier la règle de régularité dans cette suite et prolonger la suite.
Exemple
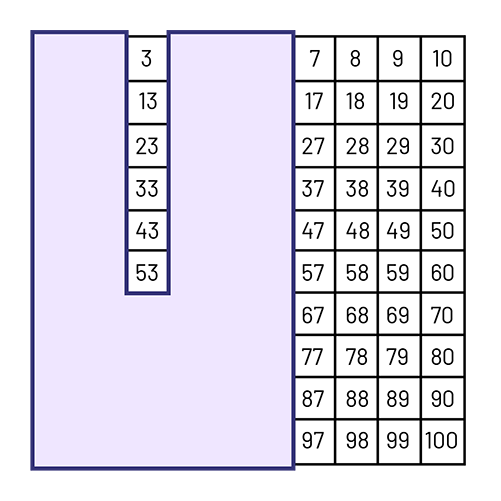Image Un tableau
numérique dont plusieurs colonnes sont masquées. Les deux premières lignes sont masquées. Une ligne est partiellement
visible. Les quatre lignes suivantes sont masquées. Enfin, les quatre dernières sont visibles.
Suite : 3, 13, 23, 33, 43, 53, 63, 73, 83, 93
Règle de régularité : +10
- Présenter des sections de la grille et repérer une suite numérique. Identifier la règle de régularité dans cette suite.
Exemple
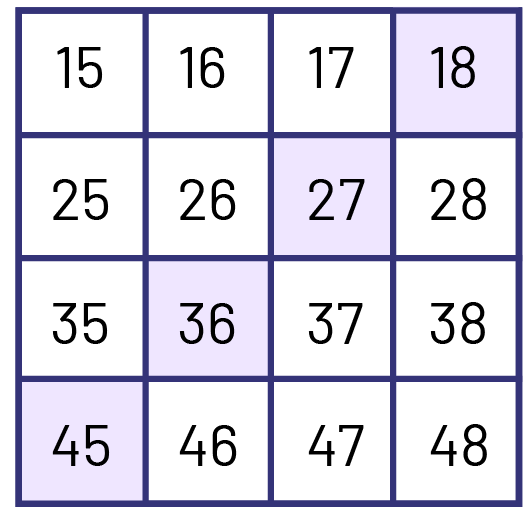Image Une grille
de nombre de 16 nombres, 4 lignes et 4 colonnes. La première ligne est : «15, 16, 17, 18. ». La deuxième ligne est
composée de « 25, 26, 27, 28. » La troisième ligne est « 35, 36, 37, 38. » Enfin, la quatrième ligne est « 45, 46, 47,
48. »
Suite : 18, 27, 36, 45
Règle de régularité : +9
Au moment de l’exploration de suites numériques à l’aide d’une grille de 100, poser aux élèves des questions afin de développer leur habileté à les représenter; par exemple :
- Que remarquez-vous au sujet des nombres identifiés dans la suite?
- Quel changement y a-t-il d’un nombre à l’autre dans chaque rangée ou chaque colonne? (Ils augmentent ou diminuent de 1 ou de 10.)
- Si les nombres n’étaient écrits que dans les trois premières rangées, que feriez-vous pour déterminer la case où se trouve le nombre 65?
- Où serait le nombre 105 si la grille était agrandie? Comment le savez-vous?
- Si le pochoir est déplacé et que le premier nombre est 5, le nombre 46 apparaîtra-t-il? Expliquez.
Droite numérique
La droite numérique est utilisée comme modèle pour faire découvrir aux élèves les régularités dans des suites. Elle permet de représenter une variété de règles. La représentation de la droite numérique peut être concrète ou semi-concrète.
Les modèles mathématiques sont des cartes mentales de relations qui peuvent être utilisées comme outil pour résoudre des problèmes. Par exemple, quand des mathématiciens pensent à un nombre, ils peuvent avoir une droite numérique en tête. Ils visualisent les nombres les uns par rapport aux autres sur la droite et ils se représentent les déplacements sur la droite.
(C. T. Fosnot et M. Dolk, Young Mathematicians at Work: Constructing Number Sense, Addition, and Subtraction, 2001, p. 77, traduction libre, cités dans ministère de l’Éducation de l’Ontario.
Voici quelques stratégies possibles pour explorer les suites numériques à l’aide d’une droite numérique :
- Au départ, utiliser une droite numérique plastifiée sur laquelle les élèves peuvent effectuer des bonds sur les nombres, à intervalles réguliers, en sautant ou au moyen d’un objet quelconque.
- À l’aide d’une droite numérique tracée sur une grande feuille de papier, les élèves encerclent les termes de la suite et indiquent, à l’aide d’une flèche, la règle de régularité dans la suite.
Au moment de l’exploration de suites numériques à l’aide d’une droite numérique, poser aux élèves des questions telles que :
- Est-ce que le nombre 58 ferait partie de la suite si la droite numérique était prolongée?
- Que remarquez-vous en ce qui a trait aux nombres encerclés sur la droite numérique?
- Quelle est la règle de régularité dans la suite? Comment est-elle indiquée?
- Si la suite débutait avec le nombre 1, qu’est-ce qui serait pareil? différent?
- Si la suite débutait avec le nombre 2, qu’est-ce qui serait pareil? différent?
Calculatrice
La calculatrice est un outil électronique qui permet aux élèves d’explorer des régularités numériques et de prolonger facilement des suites en utilisant la fonction Facteur constant. Au préalable, il est important de modeler l’entrée des données à l’aide d’une calculatrice virtuelle.
Il est important de créer une vision cohérente de ce que signifie l’alphabétisation mathématique dans un monde où les calculatrices et les ordinateurs effectuent des procédures mathématiques rapidement et où les mathématiques sont en constante évolution et appliquées dans de multiples sphères d’activité.
(National Council of Teachers of Mathematics, 1992b, p. 6, traduction libre, cité dans ministère de l’Éducation de l’Ontario.
Exemple 1
Choisir un nombre de départ entre 0 et 9. Ensuite, ajouter un nombre à ce nombre de façon continue; par exemple :
- appuyer sur la touche numérique [7];
- ajouter un intervalle de 4 en appuyant sur la touche [+], puis sur la touche numérique [4];
- appuyer sur la touche [=] à plusieurs reprises;
- écrire, au fur et à mesure, la suite numérique correspondante sur une feuille de papier (dans ce cas : 7, 11, 15, 19, 23…);
- indiquer la règle de régularité dans la suite (+4).
Poser aux élèves des questions qui les incitent à la réflexion, telles que :
- Quels chiffres apparaissent toujours dans la position des unités? Qu’est-ce qui change lorsqu’est modifié le nombre de départ ou l’intervalle choisi?
- Combien de termes contient la suite avant qu’un chiffre des unités se répète?
- Pensez-vous qu’en comptant par 4, le nombre 37 va s’afficher? Comment le savez-vous?
Exemple 2
Créer, comme dans l’exemple 1, une suite dont le nombre de départ est 23 et la règle de régularité est +12 (23, 35, 47, 59, 71…).
Poser aux élèves des questions telles que :
- Y a-t-il une règle de régularité dans cette suite? Laquelle?
- Si la suite était prolongée indéfiniment, est-ce que le nombre 155 ferait partie de cette suite? Que devez-vous faire pour le savoir?
Exemple 3
Créer, comme dans les exemples précédents, une suite dont le nombre de départ est 11 et la règle de régularité est +11 (11, 22, 33, 44, 55…).
Poser aux élèves des questions telles que :
- Si la suite est prolongée, quel sera le terme au 7e rang? Le terme au 18e rang?
- Le nombre 198 fera-t-il partie de cette suite?
Source : Guide d’enseignement efficace des mathématiques de la maternelle à la 3e année, p. 58-59.
Habileté : créer diverses suites
Avant de créer des suites, les élèves doivent d’abord reconnaître, comparer, décrire, changer la représentation et prolonger une grande variété de suites.
Les élèves démontrent leur compréhension du concept de régularité en créant une suite et en l’expliquant.
Au départ, l’utilisation du matériel de manipulation est indispensable pour représenter les suites, car au moment de la construction de suites, les élèves peuvent plus facilement changer un élément du motif et en vérifier la règle. Cependant, en dessinant la suite sur du papier, les élèves se concentrent davantage sur le dessin à reproduire plutôt que d’examiner la suite au complet et songer à la nature de la régularité.
Inviter les élèves à travailler en petits groupes afin de favoriser l’échange d’idées et leur fournir les attributs et la structure de la suite ainsi que le matériel nécessaire pour la créer.
Lors d’un échange mathématique, les présentations des suites permettent d’identifier les différentes représentations d’une même régularité et de vérifier comment les élèves communiquent leur compréhension.
Ensuite, il peut demander aux élèves de créer chacun une suite et de l’échanger avec une personne. Les élèves peuvent alors construire une différente représentation de la suite reçue, décrire sa structure, la prolonger ou en produire une complètement différente aux fins de comparaison. Il faut cependant limiter le nombre d’éléments dans le motif, car il y a des élèves qui en utilisent trop, ce qui rend difficile l’identification de la structure de la suite.
Voici quelques exemples d’activités pour créer des suites numériques :
Exemple 1
Donner aux élèves une règle de régularité d’addition ou de soustraction (par exemple, +3 ou –3). Leur demander de créer différentes suites ayant cette règle et de les comparer.
Exemple 2
Demander aux élèves de créer, sur une grille de 100, deux suites dans lesquelles on retrouve les nombres 6, 12, 24, 42 et 54, et dont la règle de régularité d’addition est autre que +1.
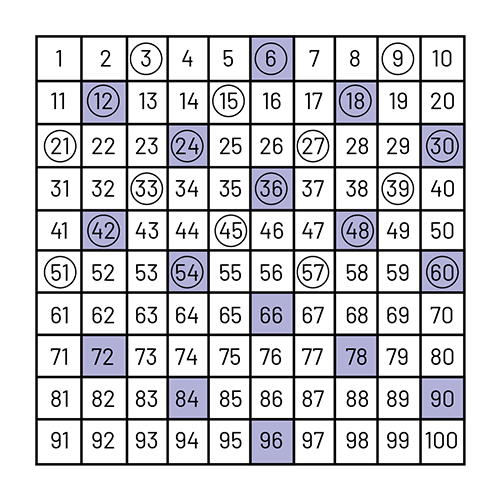
Note : Les suites possibles pour respecter les deux critères énoncés sont les suites dont la règle de régularité est +2, +3, ou +6.
Exemple 3
Demander aux élèves de créer deux suites numériques différentes dans lesquelles il y a les nombres 33 et 57, et dont la règle de régularité d’addition est autre que +1.
Solution : Les règles de régularité possibles pour créer des suites qui respectent les critères énoncés sont +2, +3, +4, +6, +8, +12 et +24.
Note : Il est important que les élèves laissent des traces de leur démarche pour s’y référer au moment de l’échange mathématique; par exemple, les élèves peuvent :
- encercler les termes de chaque suite pour les identifier;
- dessiner une flèche au-dessus de chaque bond pour indiquer l’intervalle;
- représenter symboliquement la règle de régularité à l’aide du signe +, comme dans l’exemple ci-dessous.
Solution possible
Source : Guide d’enseignement efficace des mathématiques de la maternelle à la 3e année, p. 39-40 et 63-65.
Habileté : établir des liens entre les différentes représentations
Une relation mathématique est un lien qui existe dans un contexte particulier entre des objets, des idées ou des nombres.
Les modèles mathématiques permettent d’étudier des relations. Au fil du temps, les mathématiciennes et les mathématiciens ont créé, utilisé et généralisé certaines idées, stratégies et représentations pour faciliter l’appropriation de concepts. Par l’usage, certaines représentations sont devenues des modèles reconnus, par exemple la droite numérique et le cadre à dix cases. Il est important que les élèves utilisent des modèles mathématiques dans une variété d’activités pour comprendre des relations entre les quantités.
Devant une situation-problème à résoudre, plusieurs représentations sont possibles; il y a des élèves qui utilisent leurs corps, du matériel de manipulation ou des dessins et d’autres représentent les données plus schématiquement. La façon de s’approprier les données et de les organiser à l’aide de modèles reflète le niveau de développement de la pensée algébrique. Les modèles explorés au cycle primaire et au cycle moyen seront différents selon le niveau d’abstraction des élèves. Le cadre à dix cases, la disposition rectangulaire, la table de valeurs, la droite numérique ouverte ainsi que la droite numérique ouverte double sont des modèles à favoriser au cycle primaire.
Il importe de se servir de ces modèles et d’initier les élèves à les utiliser afin de les aider à raisonner. En représentant une situation-problème, les élèves analysent les relations en se servant de modèles, tirent des conclusions et les expliquent à l’aide de descriptions orales. Les modèles sont des outils qui les aident à formaliser leur pensée algébrique.
Les modèles appliqués à plusieurs contextes favorisent l’analyse et initient les élèves à un niveau d’abstraction qui facilite les prédictions et les généralisations. Le dialogue, l’échange mathématique portant sur les données du problème représentées à l’aide de différents modèles, ainsi que le questionnement suscitent la réflexion chez les élèves.
Source : Guide d’enseignement efficace des mathématiques de la maternelle à la 3e année, p. 18-21.
La comparaison de suites permet donc une meilleure compréhension de leurs caractéristiques, favorise la réflexion, facilite la communication et permet aux élèves de développer leur raisonnement algébrique.
Source : Guide d’enseignement efficace des mathématiques de la maternelle à la 3e année, p. 59.
Suites non numériques à motif répété
L’observation de similitudes et de différences entre certaines suites consolide l’apprentissage des élèves et développe leur habileté à communiquer. Identifier deux suites qui sont semblables exige un niveau de raisonnement plus élevé, et cela aide les élèves à miser sur les relations qui existent entre les suites. La compréhension des relations est de toute première importance, car ultérieurement savoir reconnaître des relations deviendra une stratégie de résolution de problèmes.
Au moment des échanges mathématiques, il faut amener les élèves à comparer les caractéristiques particulières des suites, telles que :
- les attributs utilisés;
- le choix et la quantité d’éléments dans chaque motif;
- la structure de chaque suite;
- la règle dans chaque suite.
Exemples
| Suite 1 | Suite 2 |
|---|---|
|
|
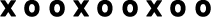
| Attributs: la forme et la couleur | Attribut : les symboles |
| Motif à 3 éléments : 1 cercle jaune et 2 trapèzes bleus | Motif à 3 éléments : un symbole x et deux symboles o |
| Structure : ABB | Structure : ABB |
| Règle de régularité : un cercle jaune suivi de deux trapèzes bleus, toujours dans le même ordre. | Règle de régularité : le symbole x suivi de deux symboles o, toujours dans le même ordre. |
L’habileté à comparer des suites facilite l’acquisition de l’habileté à les prolonger et, par la suite, à en créer de nouvelles. Pour amener les élèves à se créer une image mentale d’une régularité, il faut leur faire comparer des suites en utilisant des exemples et des non-exemples de suites. Cette stratégie leur permet de reconnaître une suite, d’en trouver la règle, de la décrire et de justifier leur raisonnement tout en utilisant un vocabulaire mathématique approprié.
Exemple d’une suite à motif répété (régularité respectée) :
Non-exemple d’une suite (aucune régularité) :
Source : Guide d’enseignement efficace des mathématiques de la maternelle à la 3e année, p. 33-34.
Suites non numériques à motif croissant
Les démarches décrites précédemment pour comparer les suites non numériques à motif répété s’appliquent aussi aux suites non numériques à motif croissant.
Source : Guide d’enseignement efficace des mathématiques de la maternelle à la 3e année, p. 40.