At a Glance...

C1.4 Create and describe patterns to illustrate relationships among whole numbers up to 100.

Skill: Creating and Representing Number Patterns Involving Whole Numbers up to 100

The base-10 system includes multiple patterns that help deepen understanding of number relationships.

Source : The Ontario Curriculum. Mathematics, Grades 1-8 Ontario Ministry of Education, 2020.

Students demonstrate their understanding of the concept of patterns by creating and explaining number patterns, such as decompositions of numbers or sets of related operations. This is an opportunity for students to make connections between positional values, as well as between addition and subtraction, and to understand the inverse relationship between these two related operations.

Teachers can offer students a whole number less than 100, such as 86, and ask them to decompose that number by position value to determine the pattern rule.

Example

86=

8 tens

+ 6 ones

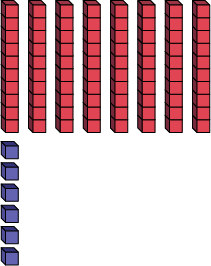
86=

7 tens

+ 16 ones

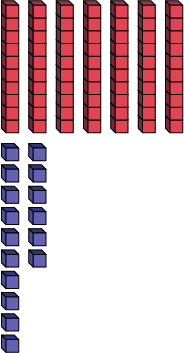
86=

6 tens

+ 26 ones

86=

5 tens

+ 36 ones

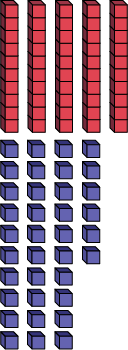
86=

4 tens

+ 46 ones

86=

3 tens

+ 56 ones

86=

2 tens

+ 66 ones

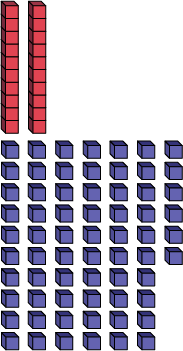
86=

1 ten

+ 76 ones

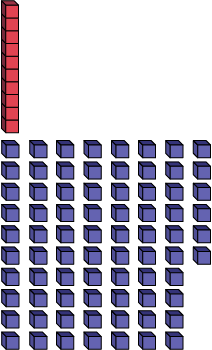
86=

0 tens

+ 86 ones

This allows students to establish the relationship between positional values (tens and units), that is., that a ten is equal to 10 units.

Have students create a pattern of operations using concrete or semi-concrete materials (for example, number grid, number lines, ten frame, interlocking cubes, base ten materials) using larger numbers. Students then exchange their set of operations with another person, build the related set with the associated subtraction facts, and finally can use this knowledge when performing calculations with larger numbers.

In this way, students notice that addition and subtraction also have an inverse relationship when the numbers are larger.

Example

Have students use their knowledge of number facts to 10 in their calculations involving larger numbers.

Example

In this way, students notice that knowledge of number facts to 10 can help them perform calculations with larger numbers.

Skill: Describing Number Patterns of Whole Numbers up to 100

By observing and analyzing the relationships between numbers within a pattern, within a number sentence, or within the base ten system, students discover patterns and can deepen their understanding of algebraic concepts.

Source : Guide d’enseignement efficace des mathématiques de la maternelle à la 3^e année, p. 16.

To get students to verbalize their observations, identify relationships, and explain how to identify the pattern rule, it is important to ask relevant questions such as:

• What do you notice?
• What is repeated?
• What do you add? What are you taking away?
• What does this number represent?
• How could you represent this number differently?
• What is the link between your two representations?
• How have the number facts you know helped you calculate larger numbers?
• How do you know that addition and subtraction are inverse operations? In what situation might this help you?

To help students establish an intuitive understanding of the structure of the pattern, teachers encourage them to verbalize the elements of the repeating pattern rule.

In the example of the number 86, students can describe the pattern of operations by explaining that the ten decreases by 1 and the units increase by 10, until there are 0 tens and 86 units.

In the example of the number 64, students can describe the inverse relationship of addition and subtraction by noticing, for example, that the numbers in the related operation are the same, but the order changes. Students can also describe the pattern rule of the addition series by noticing that the sum is always equal to 64, the first term increases by 1, and the second term decreases by 1. Students can also describe the pattern rule of the subtraction series by explaining that the difference increases by 1, the first term is always equal to 64, and the second term decreases by 1.

In the example where a number between 0 and 10 is added to the number 89, students can describe the pattern by mentioning that the first term is always 89 and the second term and the sum increase by 1. Students can also explain that they use their knowledge of number facts to add 1 to 9 to get 10 and then add the remaining units.