C1.4 Créer et décrire des suites comprenant des nombres naturels jusqu’à 100, et représenter des relations entre ces nombres.
Habileté : créer et représenter des suites numériques comprenant des nombres naturels jusqu’à 100
Le système de base dix comprend de multiples régularités et des suites qui permettent aux élèves d’approfondir leur compréhension des relations entre les nombres.
Source : Curriculum de l’Ontario, Programme-cadre de mathématiques de la 1re à la 8e année, 2020, Ministère de l’Éducation de l’Ontario.
Les élèves démontrent leur compréhension du concept de régularité en créant des suites numériques (par exemple, décompositions de nombres, séries d’opérations apparentées) et en les expliquant. Il s’agit d’une occasion pour les élèves d’établir des liens entre les valeurs de position ainsi qu’entre l’addition et la soustraction, et de comprendre la relation inverse qui existe entre ces deux opérations apparentées.
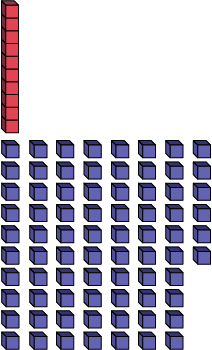
Proposer aux élèves un nombre naturel inférieur à 100, par exemple 86, et leur demander de décomposer ce nombre en fonction de la valeur de position pour déterminer la règle de régularité.
Exemple
| 86 = | 8 dizaines | + 6 unités |
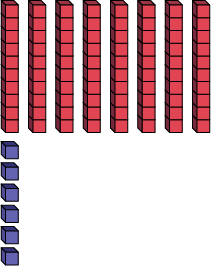
|
| 86 = | 7 dizaines | + 16 unités |
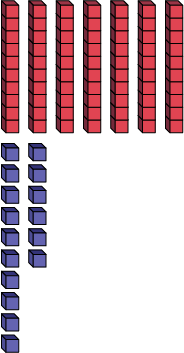
|
| 86 = | 6 dizaines | + 26 unités |

|
| 86 = | 5 dizaines | + 36 unités |
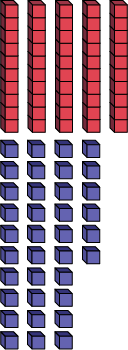
|
| 86 = | 4 dizaines | + 46 unités |

|
| 86 = | 3 dizaines | + 56 unités |

|
| 86 = | 2 dizaines | + 66 unités |
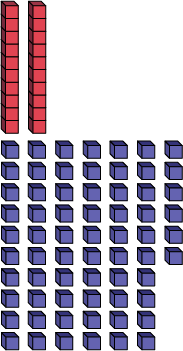
|
| 86 = | 1 dizaine | + 76 unités |
|
| 86 = | 0 dizaine | + 86 unités |

|
Les élèves peuvent ainsi établir la relation entre les valeurs de position (les dizaines et les unités), soit que une dizaine est égale à 10 unités.
Demander aux élèves de créer une suite d’opérations à l’aide de matériel concret ou semi-concret (par exemple, grille de nombres, droites numériques, cadre à dix cases, cubes emboîtables, matériel de base dix) en utilisant de plus grands nombres. Les élèves échangent ensuite leur série d’opérations avec une autre personne, puis construisent la série apparentée avec les faits de soustraction associés et, enfin, peuvent réinvestir ces connaissances au moment d’effectuer des calculs avec de plus grands nombres.
Les élèves remarquent ainsi que l’addition et la soustraction ont aussi une relation inverse lorsque les nombres sont plus grands.
Exemple
| 64 | |
|---|---|
| + | - |
| 60 + 4 = 64 | 64 – 4 = 60 |
| 61 + 3 = 64 | 64 – 3 = 61 |
| 62 + 2 = 64 | 64 – 2 = 62 |
| 63 + 1 = 64 | 64 – 1 = 63 |
| 64 + 0 = 64 | 64 – 0 = 64 |
Demander aux élèves d’utiliser leurs connaissances des faits numériques jusqu’à 10 et de réinvestir ces connaissances dans leurs calculs comportant de plus grands nombres.
Exemple
| \(\begin{align} 9 + 0 &= 9 \end{align}\) | \(\begin{align} 89 + 0 &= 89 \end{align}\) |
| \(\begin{align} 9 + 1 &= 10 \end{align}\) | \(\begin{align} 89 + 1 &= 90 \end{align}\) |
| \(\begin{align} 9 + 2 &= 9 + 1 + 1 \\ &= 11 \end{align}\) | \(\begin{align} 89 + 2 &= 89 + 1 + 1 \\ &= 91 \end{align}\) |
| \(\begin{align} 9 + 3 &= 9 + 1 + 2 \\ &= 12 \end{align}\) | \(\begin{align} 89 + 3 &= 89 + 1 + 2 \\ &= 92 \end{align}\) |
| \(\begin{align} 9 + 4 &= 9 + 1 + 3 \\ &= 13 \end{align}\) | \(\begin{align} 89 + 4 &= 89 + 1 + 3 \\ &= 93 \end{align}\) |
| \(\begin{align} 9 + 5 &= 9 + 1 + 4 \\ &= 14 \end{align}\) | \(\begin{align} 89 + 5 &= 89 + 1 + 4 \\ &= 94 \end{align}\) |
| \(\begin{align} 9 + 6 &= 9 + 1 + 5 \\ &= 15 \end{align}\) | \(\begin{align} 89 + 6 &= 9 + 1 + 5 \\ &= 95 \end{align}\) |
| \(\begin{align} 9 + 7 &= 9 + 1 + 7 \\ &= 16 \end{align}\) | \(\begin{align} 89 + 7 &= 89 + 1 + 6 \\ &= 96 \end{align}\) |
| \(\begin{align} 9 + 8 &= 9 + 1 + 7 \\ &= 17 \end{align}\) | \(\begin{align} 89 + 8 &= 89 + 1 + 7 \\ &= 97 \end{align}\) |
| \(\begin{align} 9 + 9 &= 18 \end{align}\) | \(\begin{align} 89 + 9 &= 98 \end{align}\) |
| \(\begin{align} 9 + 10 &= 19 \end{align}\) | \(\begin{align} 89 + 10 &= 99 \end{align}\) |
Les élèves remarquent ainsi que la connaissance des faits numériques jusqu’à 10 peut les aider à effectuer des calculs avec de plus grands nombres.
Habileté : décrire des suites numériques de nombres naturels jusqu’à 100
En observant et en analysant les relations entre les nombres à l’intérieur d’une suite, dans une phrase mathématique ou dans le système de base dix, les élèves découvrent des régularités et peuvent ainsi approfondir leur compréhension des concepts algébriques.
Source : Guide d’enseignement efficace des mathématiques de la maternelle à la 3e année, p. 16.
Pour amener les élèves à verbaliser leurs observations, à cerner les relations et à expliquer la façon de repérer la règle de régularité, il importe de leur poser des questions pertinentes telles que :
- Que remarques-tu?
- Qu’est-ce qui se répète?
- Qu’ajoutes-tu? Qu’enlèves-tu?
- Que représente ce nombre?
- Comment pourrais-tu représenter ce nombre différemment?
- Quel est le lien entre tes deux représentations?
- Comment les faits numériques que tu connais t’ont-ils aidé à calculer de plus grands nombres?
- Comment sais-tu que l’addition et la soustraction sont des opérations inverses? Dans quelle autre situation cela pourrait-il t’aider?
Afin d’aider les élèves à établir une compréhension intuitive de la structure de la suite, il importe de les encourager à verbaliser les éléments de la régularité qui se répète.
Dans l’exemple du nombre 86, les élèves peuvent décrire la suite d’opérations en expliquant que la dizaine diminue de 1 et que les unités augmentent de 10, jusqu’à ce qu’il y ait 0 dizaine et 86 unités.
Dans l’exemple du nombre 64, les élèves peuvent décrire la relation inverse de l’addition et de la soustraction en remarquant, par exemple, que les nombres compris dans l’opération apparentée sont les mêmes, mais que l’ordre change. Les élèves peuvent aussi décrire la règle de régularité de la série d’additions en remarquant que la somme est toujours égale à 64, que le premier terme augmente de 1 et que le deuxième terme diminue de 1. Les élèves peuvent aussi décrire la règle de régularité de la série de soustractions en expliquant que la différence augmente de 1, que le premier terme est toujours égal à 64 et que le deuxième terme diminue de 1.
Dans l’exemple où un nombre entre 0 et 10 est ajouté au nombre 89, les élèves peuvent décrire la régularité en mentionnant que le premier terme est toujours 89 et que le deuxième terme ainsi que la somme augmentent de 1. Les élèves peuvent aussi expliquer qu’elles et ils utilisent leur connaissance des faits numériques pour ajouter 1 à 9 afin d’obtenir 10 et qu’elles et ils additionnent ensuite les unités restantes.
