C1.4 Create and describe patterns to illustrate relationships among whole numbers and decimal tenths.
Activity 1: Choral Counting
Prerequisite
Before having students count in two-tenths increments, lead a mini-lesson counting in one-tenth increments.
Materials
- whiteboard or large sheet of paper
- felt-tip pens
- number line, from 0 to 5, graduated in tenths (or 10- frames where each square is considered a tenth)
Directions
- Gather the students and lead the mini-lesson.
- Tell students that they will count in two-tenths steps starting from 0 to 5.
- Allow students one minute to think about the numbers to recite.
- Then begin counting together at a pace that allows for writing the numbers. Students can be shown the visual on the number line or on the 10-frames.
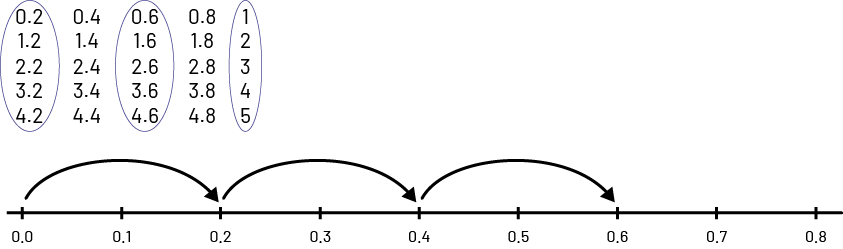
- Write the numbers, as shown below, as students recite them (two-tenths, four-tenths, six-tenths, eight-tenths).
0.2, 0.4, 0.6, 0.8
- Pause at eight tenths and ask students to think of the next number. Ask them how to pronounce and write it.
Note: Some students will think that the next number will be written as 0.10.
As you pronounce 10 tenths \(\frac{10}{10}\), write 1. Ask students why it is spelled that way. So, 10 tenths is ONE. This is best illustrated on the number line or with a filled-in 10 frame.
0,2 0,4 0,6 0,8 1
- Continue to five, writing the numbers in decimal form to show the relationships between them.
0,2 0,4 0,6 0,8 1
1,2 1,4 1,6 1,8 2
2,2 2,4 2,6 2,8 3
3,2 3,4 3,6 3,8 4
4,2 4,4 4,6 4,8 5
- Invite students to observe the written numbers after counting in two-tenths increments up to five.
- Ask students to share their observations about numbers with others in a Think-Pair-Share.
- Point out the relationships that have been observed between the numbers.
See some examples:
Suggestion
Use this opportunity to make the connection to fractions. For each decimal number recited, it is possible to write the corresponding fraction, for example, 0.2 - \(\frac{2}{10}\). Lead students to understand that decimal numbers, in tenths, can also be written as fractions with a denominator of 10. The decimal and fractional forms of a number represent the same quantity.
Activity 2: A Calculated Pattern Rule
Develop student algebraic reasoning by exploring relationships using a calculator.
Give students the following instruction:
- Press [1], [×], [10], and [=].
- Press [10,000], [÷ ], [10], and [=].
- Can you predict the next number before you press the [=] key?
- What will happen if you press the [=] key three more times?
- 10, 100, 1000, 10 000
- 10 000, 1000, 100, 10, 1, 0.1
- "For pattern (a) as each term number increases by one, the term value changes by a factor of ten."
- "For pattern (b) as each term number increases by one, the term value changes by a factor of one-tenth."
Source: translated from Guide d’enseignement efficace des mathématiques, de la maternelle à la 3e année, Modélisation et algèbre, Fascicule 1, Régularités et relations, p. 80-81.
Activity 3: Relationships in Decimal Numbers
- Present students with the following scenario:
In order to fully understand decimal numbers, Malik represents a decimal number using different related operations according to place values.
- Describe the patterns that Malik created by representing the relationship between the numbers in the related operations.
| 76.1 |
|---|
| 7 tens + 6 ones + 1 tenth |
| 6 tens + 16 ones + 1 tenth |
| 5 tens + 26 ones + 1 tenth |
| 4 tens + 36 ones + 1 tenth |
| 3 tens + 46 ones + 1 tenth |
| 2 tens + 56 ones + 1 tenth |
| 1 ten + 66 ones + 1 tenth |
| 0 tens + 76 ones + 1 tenth |
| 76.1 |
|---|
| 7 tens + 6 ones + 1 tenth |
| 7 tens + 5 ones + 11 tenths |
| 7 tens + 4 ones + 21 tenths |
| 7 tens + 3 ones + 31 tenths |
| 7 tens + 2 ones + 41 tenths |
| 7 tens + 1 one + 51 tenths |
| 7 tens + 0 one + 61 tenths |
Strategy 1
Describing patterns using words
- In Pattern A, I notice that as the tens decrease by 1, the ones increase by 10. In each ten, there are 10 ones.
- In Pattern B, I notice that as the ones decrease by 1, the tenths increase by 10. In each unit, there are 10 tenths.
Strategy 2
Describing a pattern using base ten material
- I represent the first four number sentences in Pattern A as shown below. In each ten, there are 10 ones. I notice that as the tens decrease by 1, the ones increase by 10.
Image A representation that shows us blocks of hundreds, sticks of tens and cubes of one units. Represented: One stick of tens is equal to one. 7 tens becomes 6 tens. 6 tens becomes 5 tens. 5 tens becomes 4 tens. 6 unites becomes 16 units. 16 units becomes 26 units. 26 units becomes 36 units.
- I represent the first four number sentences in Pattern B as shown below. In each one, there are 10 tenths. I notice that as the ones decrease by 1, the tenths increase by 10.
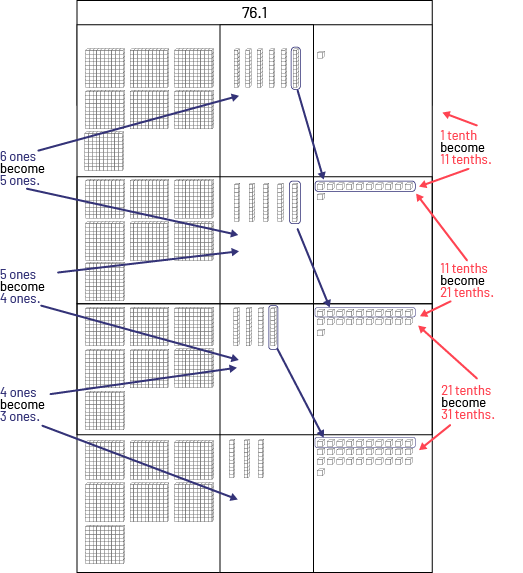Image A representation that shows us blocks of hundreds, sticks of tens and cubes of one unit. Represented: 6 unites becomes 5 units. 5 units becomes 4 units. 4 units becomes 3 units. 1 tens becomes 11 tens. 11 tens becomes 21 tens. 21 tens becomes 31 tens.
Strategy 3
Creation of series of related operations of addition and subtraction
| Addition | Subtraction |
|---|---|
| 76 + 0.1 = 76,1 | 76.1 – 1 = 75.1 |
| 75.9 + 0.2 = 76,1 | 76.1 – 0.9 = 75.2 |
| 75.8 + 0.3 = 76,1 | 76.1 – 0.8 = 75.3 |
| 75.7 + 0.4 = 76,1 | 76.1 – 0.7 = 75.4 |
| 75.6 + 0.5 = 76,1 | 76.1 – 0.6 = 75.5 |
| 75.5 + 0.6 = 76,1 | 76.1 – 0.5 = 75.6 |
| 75.4 + 0.7 = 76,1 | 76.1 – 0.4 = 75.7 |
| 75.3 + 0.8 = 76,1 | 76.1 – 0.3 = 75.8 |
| 75.2 + 0.9 = 76,1 | 76.1 – 0.2 = 75.9 |
| 75.1 + 1.0 = 76,1 | 76.1 – 0.1 = 75.10 |
Addition
I notice that when the first term decreases by 0.1 and the second term increases by 0.1, I always get the same answer throughout the series of related operations.
Subtraction
I notice that when the second term decreases by 0.1, the difference increases by 0.1.
Strategy 4
Creation of series of related operations of multiplication and division
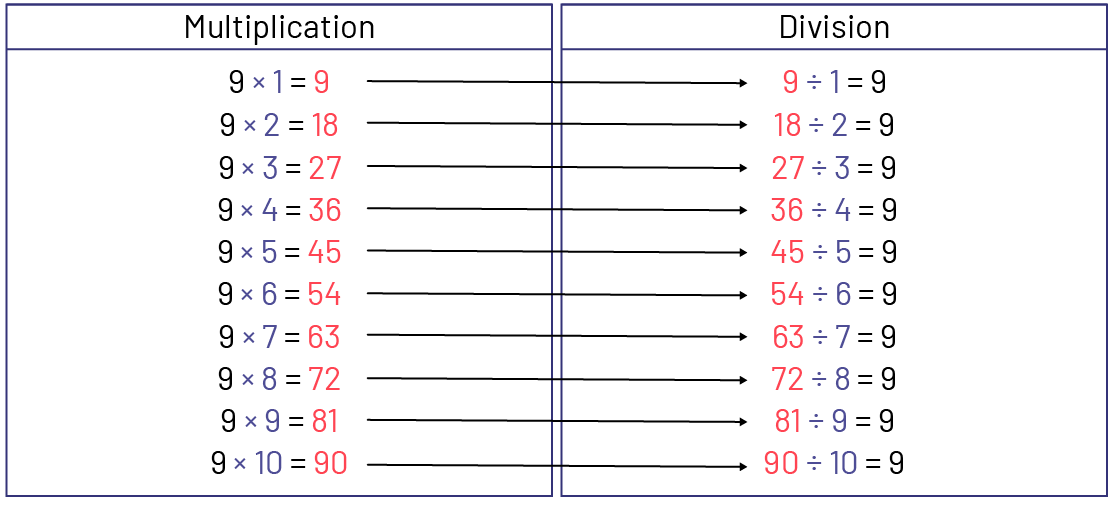
Multiplication
I notice that the product is still 9 more than the previous product.
Division
I notice that the dividend is still 9 more than the previous dividend.
Relationship between multiplication and division
I notice that division is the opposite operation of multiplication. There are always the same three numbers.
The product of the multiplication becomes the dividend of the division.
The product always increases by 9 and the dividend always increases by 9.
The second factor increases by 1 from one multiplication to the next and the divisor increases by 1 from one division to the next.
Source: translated from En avant, les maths, 4e année, Algèbre, p. 9-13.