C2.2 Solve equations that involve whole numbers up to 50 in various contexts, and verify solutions.
Activity 1: Mystery Machine
- Draw a mystery machine on the board.
Example
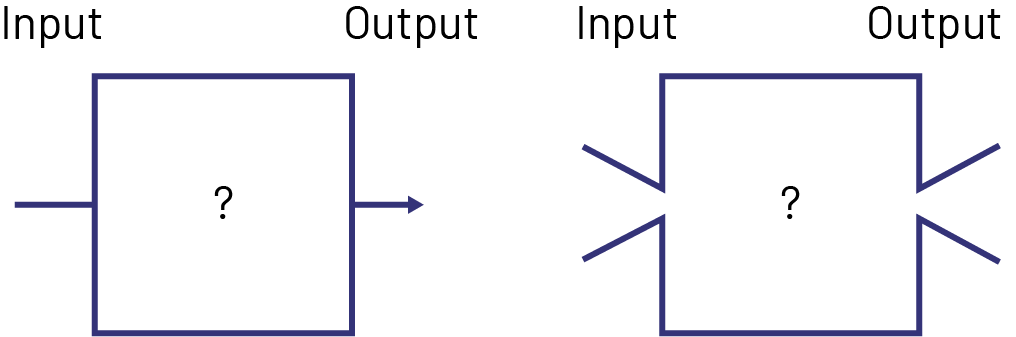
- Tell students that a mystery machine has an input and an output. Explain that a number can be entered at the input of the machine and another number can be found at the output, as a change has occurred within the mystery machine.
- Write, for example, 2 at the input of the mystery machine and 11 at the output. Invite students to analyze what is happening in the mystery machine, asking the following questions:
- What work is done in the mystery machine? (9 is added)
- What would happen if the number 4 instead of the number 2 was inserted into the mystery machine (13 would come out)
- What number must go into the mystery machine in order for 24 to come out? (15)
- Then introduce students to the following mystery machine.
- Record the inputs and outputs in a table of values.
Table of Values
| Input | Output |
|---|---|
| 3 | 9 |
| 8 | 24 |
| 5 | 15 |
- As a class, determine the change made by the mystery machine (× 3). The idea is to see the relationship between the number at the input and the number at the output.
- Suggest that students reprogram the mystery machine and present some of the numbers going in and out to the other students. They can also present the operation in the mystery machine and only the numbers going in or only the numbers coming out.
Examples
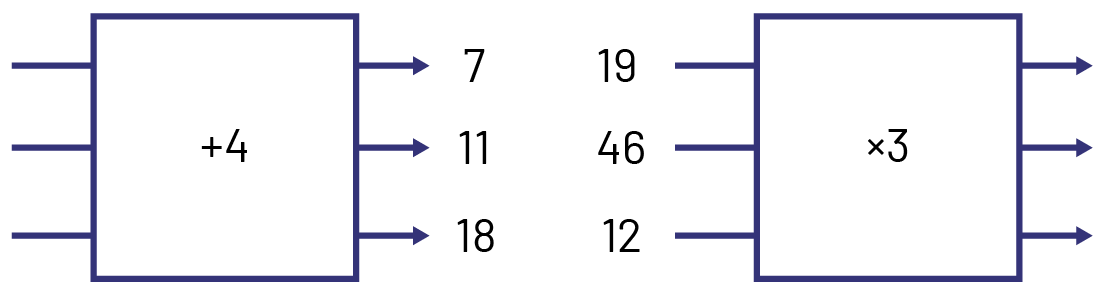Image Two drawing of mystery machines to determine the unkowns. Mystery machine one, of plus four, has entering number of 3 unknown and with exiting number of 7, 11, 17. Mystery machine 2, of multiplied by 3, has entering numbers 19, 46, and 12., and 3 unknown exiting number.
Note: In Grade 4, it is best to stick with mystery machines that perform a single operation.
Source: translated from Guide d’enseignement efficace des mathématiques de la 4e à la 6e année, Modélisation et algèbre, p. 133-134.
Activity 2: Tug of War
- Announce to the class that they will be told a silly story.
- Begin reading the story:
At a party, an elephant, four horses and five sheep meet in a park for a tug-of-war competition. They decide to play three games.
For the first game, the four horses stand on one side and the five sheep on the other. When they pull on the rope, the two teams are of equal strength.
For the second game, the elephant stands on one side, while on the other side there is a horse and two sheep. Again, the two teams are of equal strength.
For the third game, the elephant and three sheep stand on one side, while on the other side there are four horses. The whistle is blown and the battle begins. Which team will win the game?
- Group students into pairs and ask them to find the answer. Provide them with manipulatives. Ask them to leave a record of their reasoning so that they can justify their answer during the mathematical discussion.
Possible examples of student responses include:
- The sheep and the elephant will win the game because the elephant equals two sheep and one horse, so if I replace the elephant with two sheep and one horse, I have five sheep and one horse. Since five sheep are equivalent to four horses, then five sheep and one horse are stronger than four horses.
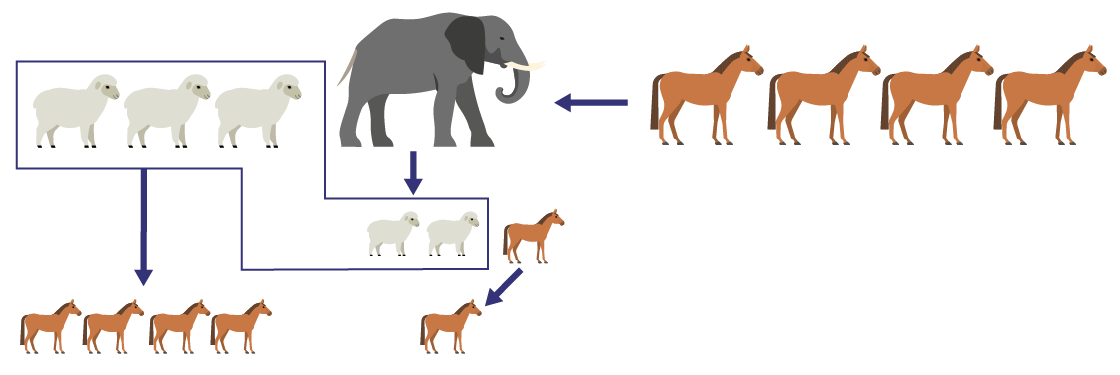Image Pattern of 3 sheep, one elephant, a rope, and four horses. An arrow showing side A will win. Arrow showing elephant is equivalent to two sheep and a horse. Another arrow show 3 sheep is equivalent to 4 horses.
- The three sheep and the elephant will win the game because four horses equal five sheep and the elephant is stronger than two sheep.
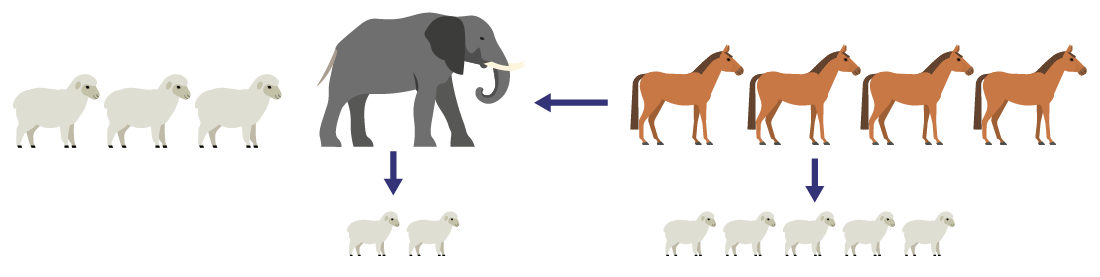Image Pattern of 3 sheep, one elephant, a rope, and four horses. An arrow is showing the right side will win. Arrow showing elephant is equivalent to 2 sheep. Another arrow showing 4 horses is equivalent to 5 sheep.
- Ask students what would need to be done to restore the equality of forces in this third part (for example, add a fifth horse on the right side, replace the elephant with two sheep).
Note: This type of activity uses algebraic and logical reasoning as well as the concepts of equality and inequality.
Source: translated from Guide d’enseignement efficace des mathématiques de la 4e à la 6e année, Modélisation et algèbre, p. 135-136.
Activity 3: Is it Equal?
Summary
In this activity, students determine the value of the unknown with concrete materials using the strategies cancel terms or equal expressions and compare terms.
Materials
- interlocking cubes of different colours (60 per team)
- sheets (one per team)
- felt-tip pens (one per team)
Directions
- Draw a open double number line. On the top of the line, place 12 interlocking cubes (10 cubes of one colour and 2 cubes of another colour). Then add 15 more cubes (10 cubes of one colour and 5 cubes of another colour) on the top part of the number line, to the right of the first 12 cubes. Finally, place 10 cubes of one colour on the bottom of the number line.
Image Growing pattern with intertwined cubes with different colours. 10 red cube and 2 blue cubes, and 10 blue cubes below. 10 red cubes and five blue cubes.
- Ask students if there are the same amount of cubes on the top part of the number line as on the bottom part of the number line. (No, the pattern of cubes on the top part of the number line is longer. Therefore, it contains more cubes.)
- Then have students symbolically write the relationship between the number of cubes on the top of the number line and the number of cubes on the bottom (12 + 15 = 10 + __).
- Finally, ask students to determine how to get the same number of cubes on both sides of the number line without removing any cubes. Ask a student to explain his or her solution.
Possible Solution
By comparing the tens on each portion of the number line, I found that there were two on the top part and one on the bottom part. So I added a ten on the bottom part of the number line.
Image Growing pattern with intertwined cubes with different colours. 10 red cube and 2 blue cubes, and 10 blue cubes below. 10 red cubes and five blue cubes, and 10 blue cubes below.
The two parts of the number line were not yet equal, so I compared the units. I discovered that there were 7 units on the upper part of the line and none on the lower part. So I added 7 units to the bottom part of the number line.
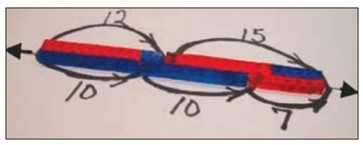
Since the two parts of the numerical line are equal, I can conclude that the value of the unknown is one ten and seven units, so 17.
- Then have students discuss different strategies that can help them determine the value of the unknown in an equation, not by calculating, but by analyzing the relationships between the quantities. Encourage them to explore strategies for cancelling terms or equal expressions and comparing terms.
Source: translated from Guide d’enseignement efficace des mathématiques de la maternelle à la 3e année, Modélisation et algèbre, Fascicule 2, Situations d'égalité, p. 182-183.