C2.2 Résoudre des équations qui comprennent des nombres naturels jusqu’à 50, dans divers contextes, et vérifier les solutions.
Activité 1 : Machine mystère
Dessiner, au tableau, une machine mystère.
Exemple
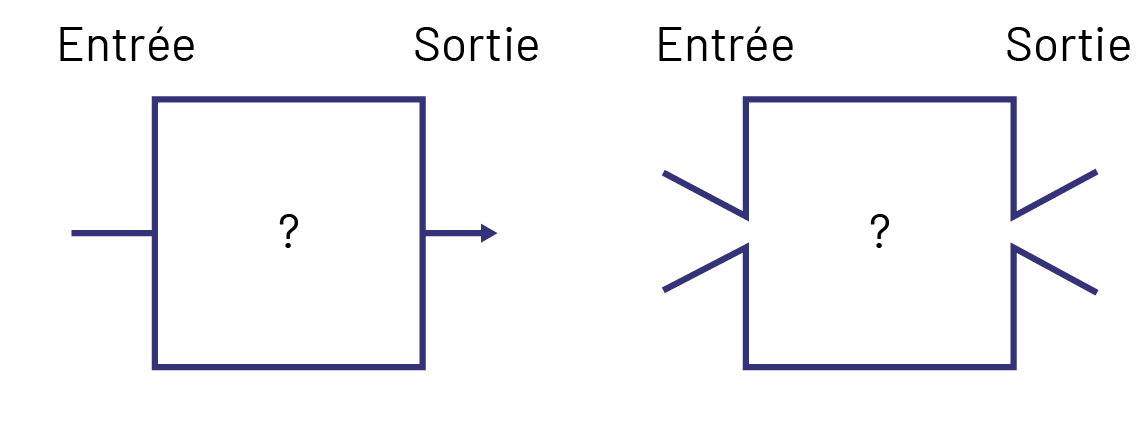
Mentionner aux élèves qu’une machine mystère est dotée d’une entrée et d’une sortie. Leur expliquer qu’on peut introduire un nombre à l’entrée de la machine et trouver un autre nombre à la sortie, un changement s’étant effectué à l’intérieur de la machine mystère.
Écrire, par exemple, 2 à l’entrée de la machine mystère et 11 à sa sortie. Inviter les élèves à analyser ce qui se passe dans la machine mystère, en leur posant les questions suivantes :
- Quel travail s’effectue dans la machine mystère? (9 est ajouté)
- Qu’arriverait-il si le nombre 4 au lieu du nombre 2 était inséré dans la machine mystère? (13 en sortirait)
- Quel nombre doit entrer dans la machine mystère afin que 24 en ressorte? (15)
Présenter ensuite aux élèves la machine mystère suivante.
Consigner dans une table de valeurs les entrées et les sorties.
Table de valeurs
| Entrée | Sortie |
|---|---|
| 3 | 9 |
| 8 | 24 |
| 5 | 15 |
Déterminer, en groupe-classe, le changement qu’a opéré la machine mystère (× 3). Il s’agit de voir la relation entre le nombre à l’entrée et celui à la sortie.
Proposer aux élèves de reprogrammer la machine mystère et de présenter aux autres élèves quelques nombres qui y entrent et y sortent. Elles et ils peuvent aussi présenter l’opération dans la machine mystère et uniquement les nombres à l’entrée ou uniquement les nombres à la sortie.
Exemples
Image
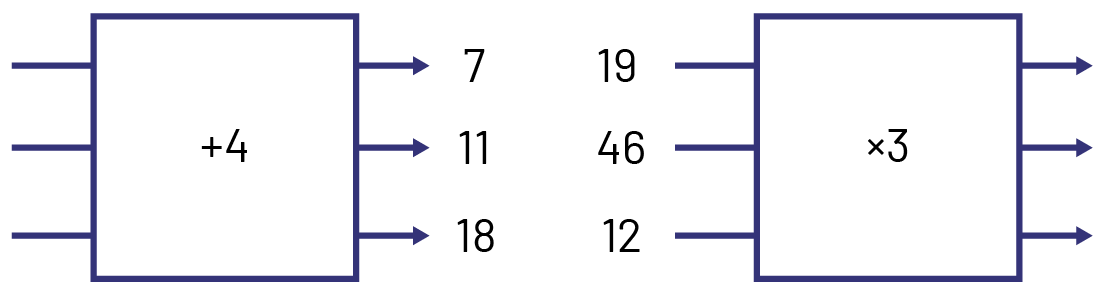
Dessin d’une machine mystérieuse, représentée par un carré « plus 4 ». Des traits dépassent à la gauche. Des flèches
sortent du carré à la droite, on peut lire 7 ,11 ,18. Dessin d’une machine mystérieuse, représentée par un carré «
multiplié par 3 ». Des traits dépassent à la gauche, on peut lire 19, 46, 12. Des flèches sortent du carré à la
droite.
Note : En 4e année, il est préférable de s’en tenir à des machines mystères qui effectuent une seule opération.
Source : Guide d’enseignement efficace des mathématiques de la 4e à la 6e année, p. 133-134.
Activité 2 : Souque à la corde
Annoncer au groupe-classe qu’une histoire farfelue leur sera racontée.
Commencer la lecture de l’histoire :
Lors d’une fête, un éléphant, quatre chevaux et cinq moutons se rencontrent dans un parc pour une compétition de souque à la corde. Ils décident de faire trois parties.
Pour la première partie, les quatre chevaux se placent d’un côté et les cinq moutons de l’autre côté. Lorsqu’elles tirent sur la corde, les deux équipes sont de force égale.
Pour la deuxième partie, l’éléphant se place d’un côté, tandis que de l’autre côté, il y a un cheval et deux moutons. Encore une fois, les deux équipes sont de force égale.
Pour la troisième partie, l’éléphant et trois moutons se placent d’un côté, tandis que de l’autre côté, il y a quatre chevaux. Le sifflet est entendu et l’affrontement commence. Quelle équipe gagnera la partie?
Grouper les élèves en équipes de deux et les inviter à trouver la réponse. Mettre à leur disposition du matériel de manipulation. Leur demander de laisser des traces de leur raisonnement afin de pouvoir justifier leur réponse au cours de l’échange mathématique.
Voici des exemples possibles de réponses d’élèves :
- Les moutons et l’éléphant gagneront la partie parce que l’éléphant équivaut à deux moutons et à un cheval, alors si je remplace l’éléphant par deux moutons et un cheval, j’ai donc cinq moutons et un cheval. Puisque cinq moutons équivalent à quatre chevaux, alors cinq moutons et un cheval sont plus forts que quatre chevaux.
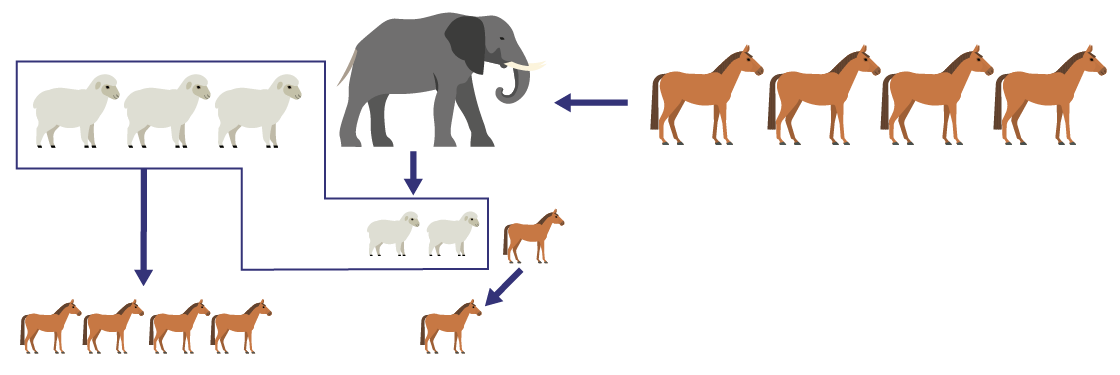
- Les trois moutons et l’éléphant gagneront la partie parce que quatre chevaux équivalent à cinq moutons et l’éléphant est plus fort que deux moutons.
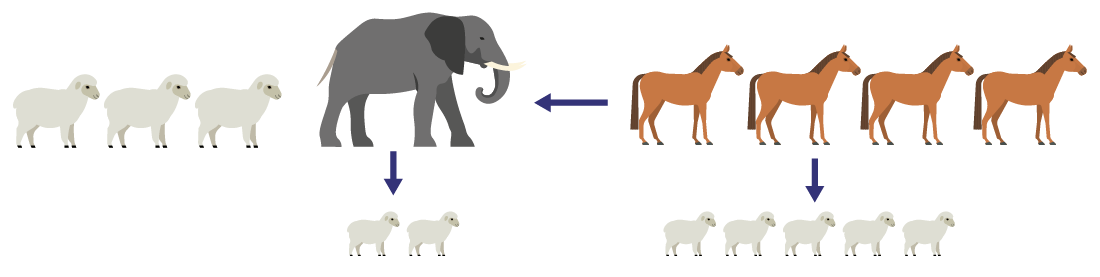
Demander aux élèves ce qu’il faudrait faire pour rétablir l’égalité des forces dans cette troisième partie (par exemple, ajouter un cinquième cheval du côté droit, remplacer l’éléphant par deux moutons).
Note : Ce type d’activité fait appel au raisonnement algébrique et logique ainsi qu’aux notions d’égalité et d’inégalité.
Source : Guide d’enseignement efficace des mathématiques de la 4e à la 6e année, p. 135-136.
Activité 3 : Est-ce égal?
Sommaire
Dans cette activité, les élèves déterminent, à l’aide de matériel concret, la valeur inconnue en utilisant les stratégies annuler des termes ou des expressions égales et comparer des termes.
Matériel
- cubes emboîtables de différentes couleurs (60 par équipe)
- feuilles (une par équipe)
- crayons-feutres (un par équipe)
Déroulement
Tracer une droite numérique ouverte double. Sur sa partie supérieure, mettre 12 cubes emboîtables (10 cubes d’une couleur et 2 cubes d’une autre couleur). Ajouter ensuite 15 autres cubes (10 cubes d’une couleur et 5 cubes d’une autre couleur) sur la partie supérieure de la droite numérique, à droite des 12 premiers cubes. Enfin, sur la partie inférieure de la droite numérique, placer 10 cubes d’une même couleur.
Demander aux élèves s’il y a la même quantité de cubes sur la partie supérieure de la droite numérique et sur la partie inférieure de celle-ci. (Non, la suite de cubes sur la partie supérieure de la droite numérique est plus longue. Elle contient donc plus de cubes.)
Inviter ensuite les élèves à écrire symboliquement la relation entre le nombre de cubes sur la partie supérieure de la droite numérique et le nombre de cubes sur la partie inférieure de celle-ci. (12 + 15 = 10 + __)
Demander enfin aux élèves de déterminer la façon de faire pour qu’il y ait le même nombre de cubes sur chacune des deux parties de la droite numérique, sans toutefois retirer de cubes. Demander à une ou à un élève d’expliquer sa solution.
Exemple de solution possible
En comparant les dizaines sur chaque portion de la droite numérique, j’ai constaté qu’il y en avait deux sur sa partie supérieure et une sur sa partie inférieure. J’ai donc ajouté une dizaine sur la partie inférieure de la droite numérique.
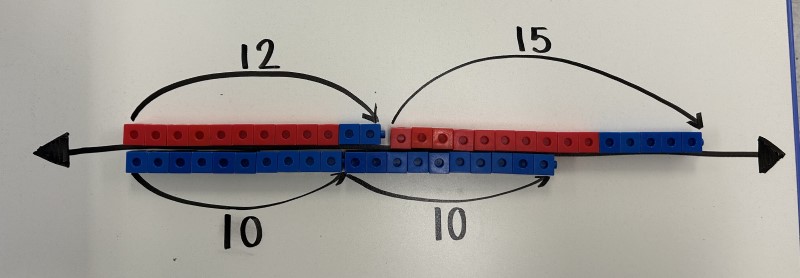Image Une
droite numérique d’un bond de plus 12 puis un bond de plus 15, représentés par des tours en blocs emboitables. 2
autres tours sont placées sur la droite, elles représentent chacune un bond de plus dix.
Les deux parties de la droite numérique n’étant pas encore égales, j’ai comparé les unités. J’ai découvert qu’il y avait 7 unités sur la partie supérieure de la droite et aucune sur sa partie inférieure. J’ai donc ajouté 7 unités sur la partie inférieure de la droite numrérique.
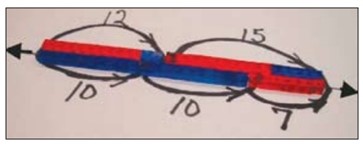Une droite
numérique d’un bond de plus 12 puis un bond de plus 15, représentés par des tours en blocs emboitables. 3 autres tours
sont placées sur la droite, les 2 premières représentent chacune un bond de plus dix. La troisième représente un bond
de plus 7.
Les deux parties de la droite numérique étant égales, je peux conclure que la valeur inconnue est de une dizaine et de sept unités, donc de 17.
Par la suite, demander aux élèves de discuter des différentes stratégies qui peuvent les aider à déterminer la valeur inconnue dans une équation, sans recourir au calcul, mais bien en analysant les relations entre les quantités. Les inciter à explorer les stratégies annuler des termes ou des expressions égales et comparer des termes.
Source : Guide d’enseignement efficace des mathématiques de la maternelle à la 3e année, p. 182-183.