C1.1 Identify and describe repeating, growing, and shrinking patterns, including patterns found in real-life contexts
Skill: Recognizing and Describing Repeating Patterns
For repeating patterns, students need to identify the beginning and the end of the core in the pattern. Students can describe that core by using letters such as AAB, AAB, AAB, etc.
Source: translated from Guide d’enseignement efficace des mathématiques de la maternelle à la 3e année, p. 30.
One way to help students "read" a pattern is to have them name and touch each consecutive element of the pattern so that they notice the repetition.
For example, in the image below, the student has created a pattern where the beginning is a yellow hexagon with an orange square on top of it and the end is two green triangles, each with one vertex touching a vertex of the other triangle.

From Kindergarten through to the end of the Junior Division, the patterns that students explore and create become increasingly complex. The following are suggestions for increasing the complexity of repeating patterns:
- Spot false leads: Recognizing that an attribute can be a false lead in a pattern. It is important for students to recognize the attribute(s) upon which the pattern is based.
- Modify the structure of the pattern: Explore more complex patterns, adding more elements to the pattern or more attributes. Students will then face a cognitive challenge that will lead to new learning.
- Change the representation: Present patterns with different representations of the same structure and check if the students recognize that they have the same structure.
- Explore patterns with a missing element in the pattern: Examining the pattern to determine what element is missing from the beginning, middle, or end of a pattern increases student understanding of relationships. Many activities like this help students understand that the pattern, as a whole, may contain several smaller repeating elements, rather than seeing it as a collection of changing elements with no relationship to each other.
Example
Pattern A

In this pattern, the colours used are not an attribute of the pattern rule. Therefore, students should eliminate the colour attribute and stick to the figure attribute (triangle, hexagon, square).
Pattern B

In this pattern, the different figures and colours create false leads that must be eliminated in order to discover the attribute (figure on a vertex with a similar figure touching it on a flat side, figure placed on a flat side).
Source: translated from Guide d’enseignement efficace des mathématiques de la maternelle à la 3e année, Modélisation et algèbre, Fascicule 1, Régularités et relations, p. 31-33.
Skill: Recognizing and Describing Growing and Shrinking Patterns
To recognize a growing geometric pattern, we must look for the relationship between each figure (pattern rule), or the pattern between the term number and the term value (functional relationship). The number of elements that make up a figure increases from one term to the next.
Source: translated from En avant, les maths!, 3e année, CM, Algèbre, p. 3.
A relationship can be represented by a pattern of concrete or semi-concrete figures or by using words. The study of relationships should first involve situations expressed using geometric representations because these representations have a visual and kinesthetic dimension that makes the relationships they represent feel less abstract.
Example of a Geometric Growing Pattern
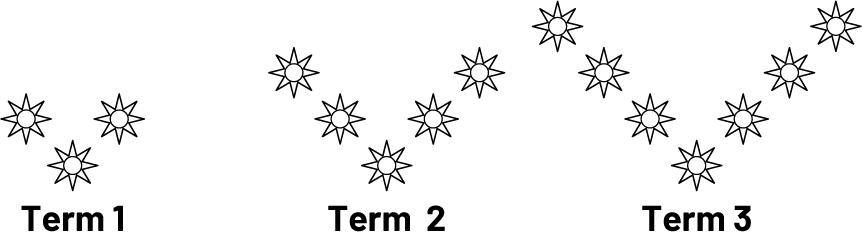
Growing geometric patterns have the following characteristics:
- The elements that make up each term in the pattern are structured to show a regularity. For example, from one term to the next in the above pattern, a sun is added at the end of each branch.
Note: Colour can be used to highlight the pattern core.

- The elements that make up each figure in the pattern can show a consistent change (e.g., a sun is added at the end of each branch), as well as the constant (e.g., three suns placed in a "V" shape).
When an increasing geometric pattern is not structured, as in the example below, it can be more difficult for students to recognize what elements are constant and what elements are increasing. Both geometric patterns have an increase in suns from one figure to the next i.e., 3, 5, 7...

Source: translated from Guide d’enseignement efficace des mathématiques de la 4e à la 6e année, Modélisation et algèbre, p. 42-43.
If the above pattern is represented in a descending order, then this pattern is considered shrinking pattern because the number of elements are decreasing from one term to the next.

Knowledge: Geometric Patterns
A series of figures or objects arranged in a particular order and showing a pattern rule from one term to the next.
Repeating Geometric Pattern
A set of figures or objects arranged in an orderly fashion, in which a repeated pattern (pattern core) can be found.
Example

Growing Geometric Pattern
A set of figures or objects arranged in which the number of elements increases one term to the next.
Example

Example 1 shows a growing pattern in which 1 square is added to each subsequent term.
Example 2 shows a spiral shell, whose 1st term (basic pattern) is the first spiral in the centre of the shell. The other terms are obtained according to a certain regularity (often associated with the Fibonacci pattern and the golden ratio). The pattern formed by the different spirals is a growing pattern because the size of the spirals increases according to a pattern rule.
Example 3 represents a pyramid, whose first term is a rectangular prism at the top, to which are added blocks whose base area grows according to a certain pattern rule.
Source: Ontario Curriculum, Mathematics Curriculum, Grades 1-8, 2020, Ontario Ministry of Education.
Shrinking Geometric Pattern
A geometric pattern that involves a decrease in the number of elements from term to term (e.g., 4 circles, 4 triangles, 3 circles, 3 triangles, ...).
Example

Knowledge: Numeric Pattern
Growing Numeric Pattern
A pattern where the terms are numbers that grow (increase). The terms of a growing number pattern come from regularities involving addition and multiplication.
Examples
- 4, 6, 8, 10... (The recursive relationship in this pattern is to add 2 to a term in order to obtain the next term)
- 1, 2, 4, 7, 11… (The recursive relationship in this pattern is to add 1 more than the previous time to get the next term)
- 3, 9, 27, 81… (The recursive relationship for this pattern is to multiply a term by 3 to get the next term)
Shrinking Numeric Pattern
A pattern where the terms are numbers that decrease by repeating subtraction of a positive or repeating multiplication by a factor between zero and one.
Examples
- 14, 11, 8… (The pattern decreases by 3 from one term to the next)
- 144, 72, 36… (The pattern decreases by one-half from one term to the next)
Knowledge: Pattern Core
Composition of the least number of elements in a pattern from which a pattern rule can be created.
Repeating Pattern

The pattern core is:

Growing Pattern

The pattern core is:

By examining each of the terms in a pattern, we can recognize that they are created by building on the pattern core, since we can see the core within each term.
Source: translated from Guide d’enseignement efficace des mathématiques de la 4e à la 6e année, Modélisation et algèbre, p. 198.
Knowledge: Attribute
A characteristic that describes an object that is observed or manipulated. Attributes can include colour, shape, texture, thickness, orientation, materials, motion, sounds, objects, or letters. The attributes that describe Pattern A below are shape and colour.
Pattern A

Non-Numeric Growing or Shrinking Pattern
In a non-numeric growing or shrinking pattern, attribute analysis is no longer important since the focus is on pattern growth.
Knowledge: Term
A term or a position number in a pattern is comprised of at least one value or element (e.g., shape, object, or motion).
Repeating Pattern
In Pattern A, each of the shapes is a term.
Pattern A

1st term:

2nd term:

3rd term:

Growing Pattern
In Pattern B, each of the shapes is a term.
Pattern B

1st term:
2nd term:
3rd term: 
Shrinking Pattern
In Pattern C, each of the shapes is a term.
Pattern C
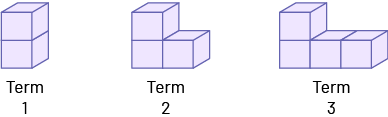
1st term: 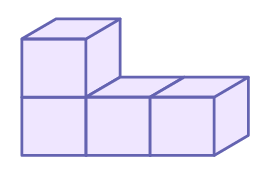
2nd term: 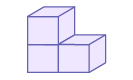
3rd term: 
Knowledge: Pattern Rules
Recursive pattern rule: a rule that is based on the relationship between one term and the next.
Repeating Pattern
Pattern rule in Pattern A: repeat the blue rectangle, green trapezoid, orange triangle pattern, always in the same order.
Note: Describing the pattern core is the pattern rule for a repeating pattern.
Pattern A

Growing Pattern
Recursive pattern rule in Pattern B: the number of squares increases by one from term to term.
Pattern B


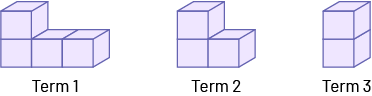
Shrinking Non-Numeric Pattern
Recursive pattern rule in Pattern C: the number of cubes increases by one from term to term.
Pattern C
Knowledge: Functional Relationship
A rule that is based on a generalization of the relationship between any term number and its associated term value.
A) Geometric Pattern and Table of Values
Pattern rule: The number of triangles in any term is three times its term number.


B) Geometric Pattern and Words
Pattern rule: For any term there is one green triangle and the number of squares is twice the term number.

|
In the 1st position, there is 1 green triangle and 1 group of 2 orange squares. In the 2nd position, there is 1 green triangle and 2 groups of 2 orange squares. In the 3rd position, there is 1 green triangle and 3 groups of 2 orange squares. In the 4th position, there is 1 green triangle and 4 groups of 2 orange squares. |
The number of shapes (f) is equal to 2 times the term number (n) plus 1: f =2n + 1
Knowledge: Structure
Letters representing the pattern rule of a repeating pattern.
In Pattern A, each element of the pattern can be identified by a letter as follows: blue rectangle (A), green trapezoid (B), orange triangle (C). The structure of Pattern A is therefore ABC.
Pattern A

Knowledge: Term
A term or a position number in a pattern is comprised of at least on value or element (e.g., shape, object, or motion).
Repeating Pattern
In Pattern A, each of the shapes is a term.
Pattern A

Growing Pattern
In Pattern B, each of the shapes is a term.
Pattern B

Shrinking Pattern
In Pattern C, each of the shapes is a term.
Pattern C

Source: translated from Guide d’enseignement efficace des mathématiques de la maternelle à la 3e année, Modélisation et algèbre, Fascicule 1, Régularités et relations, p. 29.
