C1.1 Reconnaître et décrire des suites à motif répété ainsi que des suites croissantes et des suites décroissantes, y compris des suites trouvées dans la vie quotidienne.
Habileté : reconnaître et décrire des suites à motif répété
La suite à motif répété est la forme de suite la plus simple. Pour la reconnaître, il faut chercher la règle de régularité. Elle se crée lorsque les éléments qui constituent le motif se répètent selon le même ordre. Les élèves doivent apprendre à déterminer le début et la fin du motif dans la suite.
En outre, il est important de demander aux élèves de « lire » la suite en nommant et en touchant chaque élément consécutif du motif pour qu’elles et ils se rendent compte de la répétition.
Par exemple, dans l’image ci-dessous, l’élève a créé une suite dont le début est un hexagone jaune avec un carré orange par-dessus et la fin est deux triangles verts dont les sommets se touchent.

Du cycle préparatoire jusqu’à la fin du cycle moyen, les suites que les élèves apprennent à explorer et à créer doivent être de plus en plus complexes. Pour enseigner les suites à motif répété :
- Modifier la structure de la suite : Explorer des suites plus complexes, en ajoutant plus d’éléments au motif ou plus d’attributs. Les élèves feront alors face à un défi cognitif qui les mènera à un nouvel apprentissage.
- Changer le mode de représentation : Présenter des suites ayant la même structure, mais créées selon différents modes de représentations et vérifier si les élèves reconnaissent qu’elles ont la même structure.
- Explorer des suites ayant un élément manquant dans le motif : Examiner la suite pour déterminer l’élément qui manque au début, au milieu ou à la fin d’un motif augmente leur compréhension des relations. Plusieurs activités de ce genre aident les élèves à comprendre la suite comme étant un tout qui contient plusieurs motifs, au lieu d’une séquence d’éléments changeants sans aucune relation entre eux.
- Repérer des fausses pistes : Reconnaître qu’un attribut peut être une fausse piste dans une suite contribue au développement du raisonnement algébrique.
Exemples
Suite A
 image Suite
« A »:Un hexagone rouge avec un carré orange par-dessus et la fin est deux triangles verts dont les sommets se
touchent.Un hexagone jaune avec un carré beige par-dessus et la fin est deux triangles verts dont les sommets se
touchent.Un hexagone bleu avec un carré vert par-dessus et la fin est deux triangles verts dont les sommets se
touchent.
image Suite
« A »:Un hexagone rouge avec un carré orange par-dessus et la fin est deux triangles verts dont les sommets se
touchent.Un hexagone jaune avec un carré beige par-dessus et la fin est deux triangles verts dont les sommets se
touchent.Un hexagone bleu avec un carré vert par-dessus et la fin est deux triangles verts dont les sommets se
touchent.
Dans cette suite, les couleurs utilisées ne sont pas un attribut de la règle de régularité. Les élèves doivent donc éliminer l’attribut couleur et s’en tenir à l’attribut forme (triangle, hexagone, carré).
Suite B

Dans cette suite, les différentes formes et couleurs créent de fausses pistes qui doivent être éliminées afin de découvrir l’attribut, soit la position de la base (figure placée sur un sommet avec une figure pareille qui la touche sur un côté plat, figure placée sur un côté plat).
Source : Guide d’enseignement efficace des mathématiques de la maternelle à la 3e année, p. 30-33.
Habileté : reconnaître et décrire des suites croissantes et décroissantes
Pour reconnaître une suite croissante, il faut chercher la relation entre chaque terme (règle de régularité) ou entre le rang de chaque terme et le nombre d’éléments dans le terme ou la figure (règle de correspondance). Le nombre d’éléments qui composent une figure augmente d’un rang à l’autre.
Source : En avant, les maths!, 3e année, CM, Algèbre, p. 3.
Une relation peut être représentée par une situation qui est exprimée à l’aide d’une suite de figures concrètes ou semi-concrètes ou à l’aide de mots. L’étude des relations devrait d’abord passer par des situations exprimées à l’aide de suites non numériques parce que ces situations possèdent une dimension visuelle et kinesthésique qui rend les relations qu’elles représentent moins abstraites.
Exemple d’une suite non numérique à motif croissant
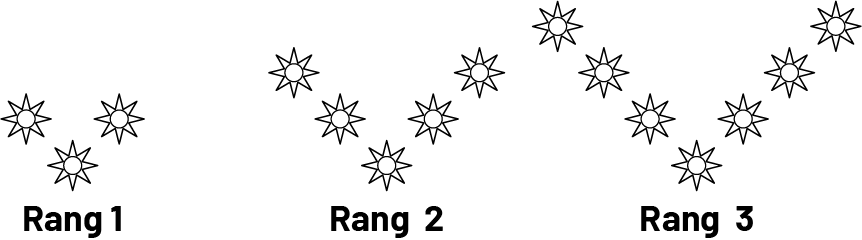
Les suites non numériques croissantes présentent les caractéristiques suivantes:
- Les éléments qui composent chaque figure de la suite sont disposés selon un ordre et une règle. Par exemple, d’un rang à l’autre dans la suite ci-dessus, on ajoute un soleil au bout de chaque branche.
- Le motif est repérable dans chaque figure, de manière que chaque figure provient de la croissance de la figure située au rang précédent. Par exemple, dans la suite ci-dessus, le motif de base est formé de trois soleils placés en forme de « V ».
Note : On peut utiliser de la couleur afin de faire ressortir le motif de base.

- Le nombre et l’emplacement des éléments qui composent chaque figure sont prévisibles. Par exemple, dans la suite ci-dessus, on peut prévoir que la figure située au 5e rang sera composée du motif de base, soit trois soleils placés en forme de « V », et de quatre soleils de plus sur chaque branche. Elle sera donc composée de 11 soleils en tout.
Une bonne connaissance des caractéristiques d’une suite non numérique croissante et décroissante permet aux élèves de reconnaître ces types de suite. Les élèves peuvent en effet reconnaître, par exemple, que la suite suivante n’est pas une suite non numérique à motif croissant, même si chaque figure est composée de la même quantité de soleils que dans la suite précédente, soit 3, 5, 7…, car ceux-ci ne sont pas disposés selon un ordre et une règle qui permettent de prévoir l’emplacement des soleils qui composeront la figure au prochain rang.

Source : Guide d’enseignement efficace des mathématiques de la 4e à la 6e année, p. 42-43.
Si les mêmes illustrations sont présentées sous forme décroissante, l’élève peut aussi constater qu’elles ne sont pas considérées comme étant une suite non numérique décroissante. Comme l’exemple ci-dessus, les figures ne sont pas disposées selon un ordre et une règle qui permettent de prévoir l’emplacement des soleils qui composeront la figure au prochain rang.

Connaissance : suite non numérique
Ensemble de figures ou d’objets disposés selon un ordre et habituellement soumis à une règle.
Source : Curriculum de l’Ontario. Programme-cadre de mathématiques de la 1re à la 8e année, 2020, Ministère de l’Éducation de l’Ontario.
Suite à motif répété
Ensemble de figures ou d’objets disposés selon un ordre et une régularité, dans lequel se répète un motif.
Exemple

Suite croissante
Ensemble de figures ou d’objets, disposés selon un ordre et une régularité, dans lequel on distingue un motif de base qui croît d’un rang à l'autre.
Exemple
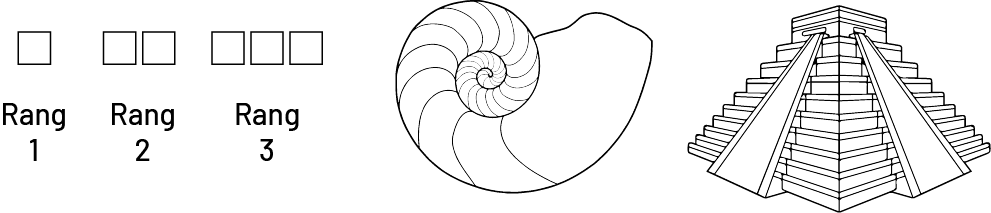
Le premier exemple représente une suite croissante. Le motif de base est un carré auquel un carré est ajouté à
chaque rang subséquent.
Le deuxième exemple représente un coquillage en spirale, dont le premier rang (motif de base) est la première spirale au centre du coquillage. Les termes aux autres rangs s’obtiennent selon une certaine régularité (souvent associé à la suite de Fibonacci et au nombre d’or). La suite que forment les différentes spirales est croissante, car la grosseur des spirales augmente selon une régularité.
Le troisième exemple représente une pyramide, dont le terme au premier rang est un prisme rectangulaire au sommet, auquel lui sont ajoutées des pierres dont l’aire de la base croît selon une certaine régularité.
Source : Curriculum de l’Ontario. Programme-cadre de mathématiques de la 1re à la 8e année, 2020, Ministère de l’Éducation de l’Ontario.
Suite décroissante
Ensemble de figures ou d’objets, disposés selon un ordre et une régularité, qui implique une régression (par exemple, une diminution du nombre d’éléments) d’un rang à l’autre.
Exemple

Connaissance : suite numérique
Suite numérique croissante : Suite où les termes sont des nombres qui croissent (augmentent). Les termes d’une suite croissante proviennent de règles de régularité liées à l’addition et à la multiplication.
Exemples
- 4, 6, 8, 10... (La règle de régularité de cette suite est d’additionner 2 afin d’obtenir le terme au rang subséquent.)
- 1, 2, 4, 7, 11… (La règle de régularité de cette suite est d’additionner 1 de plus que la fois précédente afin d’obtenir le terme au rang subséquent.)
- 3, 9, 27, 81… (La règle de régularité de cette suite est de multiplier par 3 afin d’obtenir le terme au rang subséquent.)
Suite numérique décroissante : Suite où les termes sont des nombres qui diminuent. Les termes d’une suite décroissante proviennent de règles de régularité liées à la soustraction et à la division.
Exemples
- 14, 11, 8… (La règle de régularité de cette suite est de soustraire 3 afin d’obtenir le terme au rang subséquent.)
- 144, 72, 36… (La règle de régularité de cette suite est de diviser par 2 afin d’obtenir le terme au rang subséquent.)
Connaissance : motif
La plus petite partie d’une suite non numérique à partir de laquelle la règle de régularité est créée.
Suite à motif répété

Le motif est : 
Suite croissante

Le motif est : 
En examinant chacune des figures de la suite, on peut reconnaître qu’elles sont créées en relation avec le motif, puisqu’on peut le repérer à l’intérieur de chaque figure.
Source : Guide d’enseignement efficace des mathématiques de la 4e à la 6e année, p. 198.
Connaissance : attribut
Suite à motif répété
Propriété observable d’une personne ou d’un objet. Les attributs peuvent inclure la couleur, la forme, la texture, l’épaisseur, l’orientation, les matériaux, les mouvements, les sons, les objets ou les lettres. L’attribut est reflété dans un objet par une caractéristique. Par exemple, si l’attribut est la couleur, les caractéristiques peuvent être rouge, bleu, jaune.
Dans la suite A, les attributs qui décrivent la suite sont la forme et la couleur. Les caractéristiques de la forme sont le rectangle, le trapèze et le triangle. Les caractéristiques de la couleur sont bleu, vert et orange.
Suite A

Suite non numérique à motif croissant ou décroissant
Dans une suite non numérique à motif croissant ou décroissant, l’analyse des attributs n’est plus importante puisque l’accent est mis sur la croissance du motif ou sur la décroissance d’un rang à l’autre.
Connaissance : terme
Chaque figure, objet, mouvement qui compose une suite non numérique ou chaque nombre qui compose une suite numérique.
Suite à motif répété
Dans la suite A, chacune des figures planes est un terme.
Suite A

1er terme :

2e terme :

3e terme :

Suite croissante
Dans la suite B, chacune des figures est un terme.
Suite B

1er terme :
2e terme :
3e terme : 
Suite décroissante
Dans la suite C, chacune des figures est un terme.
Suite C
Connaissance : règle de régularité
Règle qui permet de prolonger une suite en respectant la différence entre les termes (aussi appelé bond constant).
Suite à motif répété
Règle de régularité dans la suite A : répétition du motif rectangle bleu, trapèze vert, triangle orange, et ce, toujours dans le même ordre.
Suite A

Suite non numérique croissante
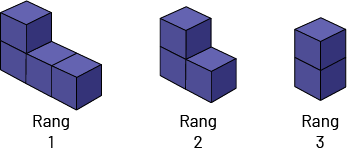
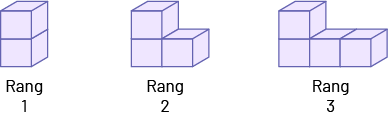
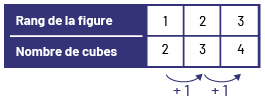
Règle de régularité dans la suite C : un cube est toujours ajouté à la rangée du bas du rang précédent.
Suite C
Suite non numérique décroissante
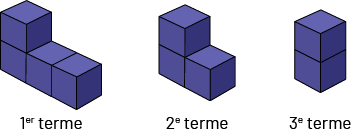
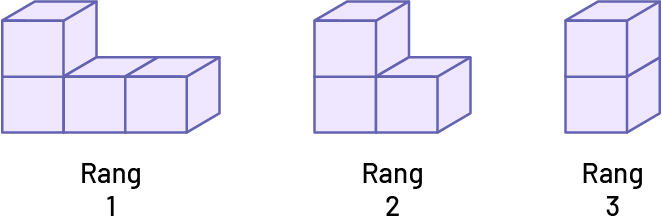
Régle de régularité dans la suite D : un cube est toujours enlevé à la rangée du bas de la figure au rang précédent.
Suite D
Connaissance : règle de correspondance
Règle qui permet de prolonger une suite en établissant la relation entre le rang et son terme.
Dans la suite ci-bas, la règle de correspondance est que le nombre de triangles dans la figure est 3 fois plus que son rang.
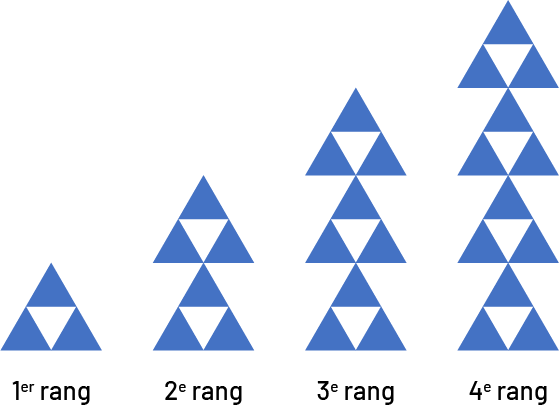
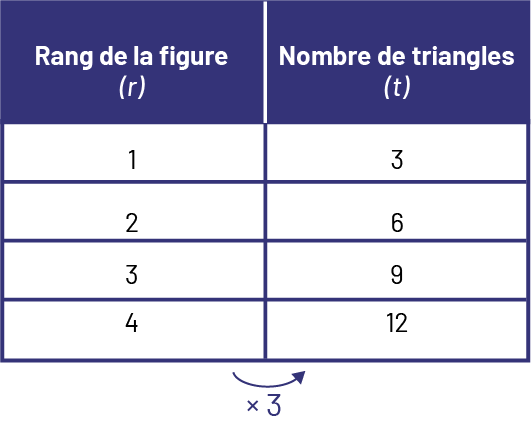
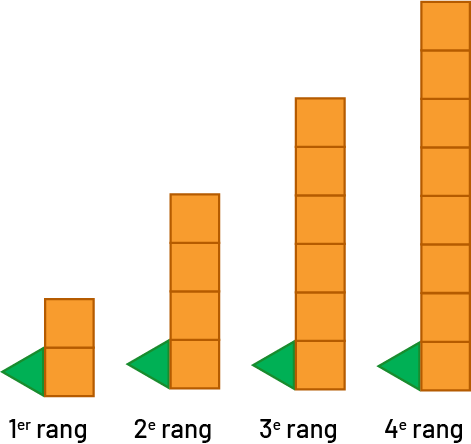
Dans cette prochaine suite, le triangle vert est constant d’un rang à l’autre et le nombre de groupes de 2 carrés orange correspond au rang de la figure.
|
Au 1er rang, il y a 1 triangle vert et 1 groupe de 2 carrés orange. Au 2e rang, il y a 1 triangle vert et 2 groupes de 2 carrés orange. Au 3e rang, il y a 1 triangle vert et 3 groupes de 2 carrés orange. Au 4e rang, il y a 1 triangle vert et 4 groupes de 2 carrés orange. |
Connaissance : structure
Représentation à l’aide de lettres de la régularité d’une suite à motif répété.
Dans la suite A, chaque élément du motif peut être identifié par une lettre comme suit : rectangle bleu (A), trapèze vert (B), triangle orange (C). La structure de la suite A est donc ABC.
Suite A

Connaissance : rang
Position qu’occupe chaque terme dans une suite. Le rang est indiqué par un nombre. Il est utilisé pour aider à décrire les relations dans une suite et à prédire les prochains termes dans la suite sans avoir à la prolonger.
Suite à motif répété
Dans la suite A, on trouve un rectangle bleu au 1er rang, au 4e rang et au 7e rang, un trapèze vert au 2e rang, au 5e rang et au 8e rang, etc.
Suite A

Suite non numérique croissante
Dans la suite B, chaque figure a son rang : la figure 1 occupe le 1er rang, la figure 2 occupe le 2e rang, etc.
Suite B

Suite non numérique décroissante
Dans la suite C, chaque figure a son rang : la figure 1 occupe le 1er rang, la figure 2 occupe le 2e rang, etc.
Suite C

Source : Guide d’enseignement efficace des mathématiques de la maternelle à la 3e année, p. 29.
