C1.2 Create and translate growing and shrinking patterns using various representations, including tables of values and graphs
Skill: Creating Growing and Shrinking Patterns
Before creating patterns, students must first recognize, compare, describe, change the representation, and extend a wide variety of patterns.
Below is an example in which students demonstrate their understanding of the concept of a rule by creating a pattern and explaining it:
When students use manipulatives to create patterns they can easily change one element of the pattern and check the rule.
Initially, teachers have students work in small groups to encourage the exchange of ideas. They can provide them with the attributes and structure of the pattern, as well as the materials required to create it.
During a mathematical discussion (consolidation/debrief), presentations of the patterns help to identify different representations of the same rule and to check how students communicate their understanding.
Next, students can be asked to create a pattern and exchange it with a peer. They can then construct a different representation of the received pattern, describe its structure, extend it, or produce a completely different one for comparison. The number of elements in the pattern should be limited, however, as some students use too many, making it difficult to understand the structure of the pattern.
Source: translated from Guide d’enseignement efficace des mathématiques de la maternelle à la 3e année, Modélisation et algèbre, Fascicule 1, Régularités et relations, p. 39-41.
Example
Provide a recursive relationship of addition or subtraction (for example., +23 or -23). Have students create different patterns with this relationship and compare them.
Source: translated from Guide d’enseignement efficace des mathématiques de la maternelle à la 3e année, Modélisation et algèbre, Fascicule 1, Régularités et relations, p. 63.
Skill: Representing Patterns and Making Connections Between Different Representations
When students make connections betweeen the different representations they are deepening their understanding about a pattern. When students express their understanding of a problem situation or concept and defend their ideas using different representations they are demonstrating their algebraic reasoning.
Modes of representations
- concrete, related to exploration, manipulation and creation using concrete materials;
- visual or semi-concrete, related to an illustration, drawing or other representation on paper;
- symbolic, related to any representation made from numbers or symbols;
- "with words", linked to a verbal or written explanation or description.
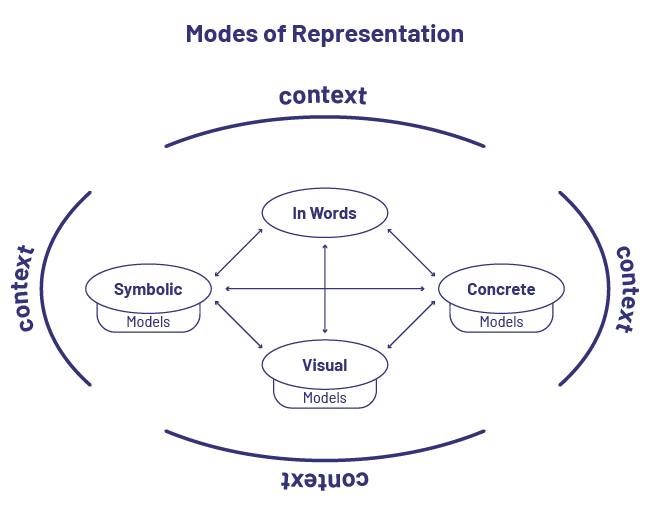
Source: translated from Guide d’enseignement efficace des mathématiques de la 4e à la 6e année, Modélisation et algèbre, p. 18.
Contexts allows students to make connections between the various representations.
In the junior grades, students explore patterns and represent them in different ways. In Grade 5, students learn that a growing pattern can be represented by a situation (non-numeric pattern), a word rule, a table of values, or a graphical representation. The arrows in the graph below show the connections between these representations.
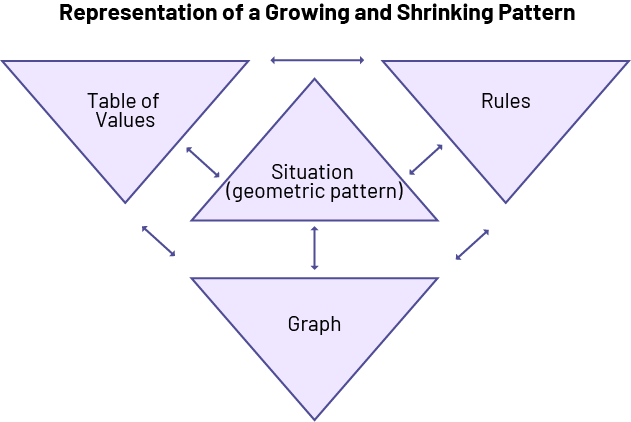
Source: translated from Guide d’enseignement efficace des mathématiques de la 4e à la 6e année, Modélisation et algèbre, p. 41.
Using multiple representations of the same pattern to communicate understanding is an essential component of developing algebraic thinking.
Describing a shrinking pattern
When students are presented with a shrinking pattern, teachers should provide them with a variety of opportunities to describe it in words. This is an essential step in getting students to determine the algebraic expression of the pattern.
The shrinking pattern can be described as follows:
- Term 1 is composed of 3 blue squares and 8 red circles.
- Term 2 is composed of 3 blue squares and 7 red circles.
- Term 3 is composed of 3 blue squares and 6 red circles.
Students may also notice that the number of blue squares, 3, remains constant, while the number of red circles decreases by 1 for each term.

Manipulatives
The manipulatives (for example, algebraic tiles, nesting cubes, tokens, relational rods) are quite varied. Using them helps students explore, represent, and make changes easily during trials. The following are examples of how manipulatives can be used.
Representing a Shrinking Pattern Using Manipulatives
Have students represent the 14, 10, 6, 2 number pattern in a concrete way to make the pattern more visible by creating a shrinking pattern using manipulatives of their choice.
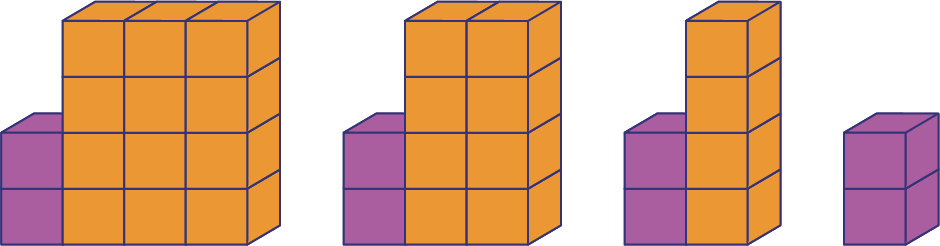
Relevant Questions
- How many cubes (tokens, blocks …) will you use to concretely represent the first term of the pattern? The second? The third?…
- What change do you notice from one term to the next?
- What does not change from one term to the next (the constant)?
- What is the pattern rule? How do you know?
Source: translated from Guide d’enseignement efficace des mathématiques de la 4e à la 6e année, Modélisation et algèbre, p. 212.
Illustration
Drawing an illustration allows students to create a semi-concrete personal representation of their observations and understanding.
Many types of problems are naturally suited for students to draw a picture to help them solve the problem. Students may also use manipulatives at the same time.
Here are some examples of how a drawing can be used:
Representing a Growing Pattern Using an Illustration
Present students with the following situation:
| Weeks | 1 | 2 | 3 | 4 | ||
|---|---|---|---|---|---|---|
| Amount in the Piggy Bank ($) | 5 | 9 | 13 | 17 |
Ask students to illustrate the situation and determine how much money the parents give him each week.

Relevant Questions
- How does the illustration help determine the pattern rule?
- How much money will Simon have in the piggy bank in week 5? How do you know?
- If Simon receives the same amount of money each week, why does he have $5 after the first week?
- How can you determine the amount in the piggy bank after many weeks have past, for example, in week 10?
- After how many weeks will Simon have enough money to buy a video game for $45 (including taxes)?
Source: translated from Guide d’enseignement efficace des mathématiques de la 4e à la 6e année, Modélisation et algèbre, p. 214-215.
Table of Values
A table of values is a semi-concrete representation showing the relationship between two changing quantities (variables), one of which depends on the other. It is often constructed to represent the relationship between numerical values associated with the terms of a growing or shrinking pattern.
The table of values can also be used to present values of variables in an equation or in a problem-solving context.
Representing a Situation Using a Table of Values
In a problem-solving context, students can also relate a situation expressed in words to a table of values.
Present the following problem situation:
Students can first use a table of values to represent the relationship between the number of movies viewed and the amount of money spent.
| Number of Movies Rented | Cost ($) |
|---|---|
| 1 | 9 |
| 2 | 14 |
| 3 | 19 |
| 4 | 24 |
| ... | ... |
To better understand this relationship, students can model it using concrete or semi-concrete materials and words.

|
When you rent 1 movie, there is a $4 subscription fee and 1 x $5, so you pay $9. When you rent 2 movies, there is a $4 subscription fee and 2 x $5, so you pay $14. When you rent 3 movies, there is a $4 subscription fee and 3 x $5, so you pay $19. When you rent 4 movies, there is a $4 subscription fee and 4 x $5, so you pay $24. |
Afterwards, students can use a table of values to represent the relationship between the number of movies rented and the amount of money spent.
| Number of Movies Rented | Amount Spent ($) |
|---|---|
| 1 | 9 |
| 2 | 14 |
| 3 | 19 |
| 4 | 24 |
| ... | ... |
Source: translated from Guide d’enseignement efficace des mathématiques de la 4e à la 6e année, Modélisation et algèbre, p. 51.
Graphical Representation
A graph is a set of point (term number, term value) plotted on a coordinate system.
Represent the Relationship Between Two Changing Quantities Using a Graph
Present the following situation:
| Number of Pitchers Sold | 1 | 2 | 3 | ||
|---|---|---|---|---|---|
| Amount Collected ($) | 4 | 8 | 12 |
Then graph the data as shown below.

Source: translated from Guide d’enseignement efficace des mathématiques de la 4e à la 6e année, Modélisation et algèbre, p. 233.
Relevant questions
- What changes are there from pitcher to pitcher in terms of sales? Are these changes always the same? Why or why not?
- Looking at the chart, how is it possible to determine the next cash inflow?
- What is the relationship between the number of pitchers sold and the amount collected?
- How can the first three values shown in the diagram help you determine the amount of money collected after eight pitchers are sold?
Represent the Relationship Between Two Changing Quantities Using a Bar Graph
Present the following situation:
With the students, represent the gardens with an illustration.
Example

Using a table of values, represent the relationship between the the number of square spaces a garden occupies and its perimeter.
| Number of Square Spaces | Perimeter (m) |
|---|---|
| 1 | 4 |
| 2 | 6 |
| 3 | 8 |
Then graph the data as shown below.
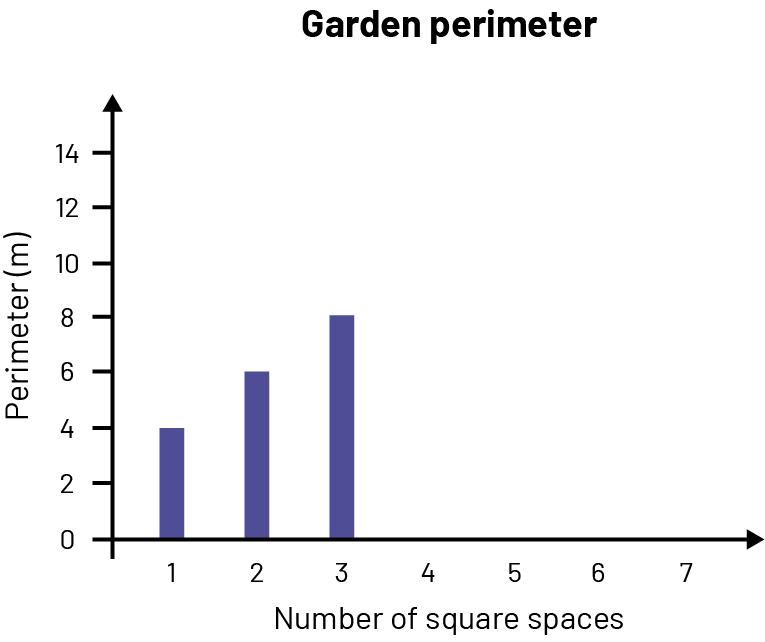
Relevant Questions
- What change is there between the values of the number of square spaces? Between the values of the perimeters? Explain your reasoning.
- What would be the next entries in the table of values?
- What is the relationship between the number of square spaces a garden occupies and the perimeter of the garden?
- How could you use the graph to determine the perimeter of an 8 square space garden?
- How many square spaces does a garden with a perimeter of 16 m occupy?
Source: translated from Guide d’enseignement efficace des mathématiques de la 4e à la 6e année, Modélisation et algèbre, p. 234-235.
Knowledge: Table of Values
The table of values is a numerical representation of the relationship between two variables, in which one variable is independent and the other variable is dependent. By the end of the primary grades, students have learned to create tables of values to represent relationships in problem situations.
The table of values is often created to represent the relationship between term numbers and term values of growing and shrinking patterns.
Example
The table of values below is displaying the term number in the first column (or row) and the number of objects (term value) in the second column (or row). The pattern rule can be used to extend the table of values.
The table of values can be arranged vertically or horizontally and is separated into columns or rows. It is a good idea to vary the layout of the table of values so that students get used to both layouts.
Vertical Table of Values
| Term Number | Number of Objects |
|---|---|
| 1 | 2 |
| 2 | 4 |
| 3 | 6 |
| 4 | … |
Horizontal Table of Values
| Term Number | 1 | 2 | 3 |
|---|---|---|---|
| Number of Objects | 2 | 4 | 6 |
Source: translated from Guide d’enseignement efficace des mathématiques de la 4e à la 6e année, Modélisation et algèbre, p. 231.
Knowledge: Graphical Representation
The term numbers are represented on the horizontal axis. The term value is represented on the vertical axis. The term value for term 0 is a point on the vertical axis.
Source: translated from Guide d’enseignement efficace des mathématiques de la 7e à la 10e année, Fascicule 2, Algèbre, p. 63.
Example
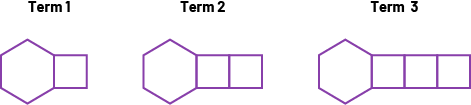
Relationship between the term number and the number of toothpicks to create each figure (term value) is shown in the graph below.
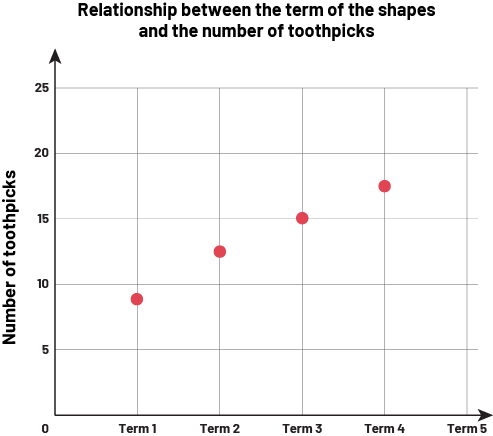
Source: translated from En avant, les maths, 6e année, Algèbre, Habiletés liées aux relations dans les suites, p. 5-6.
