C1.2 Créer des suites croissantes et des suites décroissantes, à l’aide d’une variété de représentations, y compris des tables de valeurs et des représentations graphiques, et établir des liens entre les différentes représentations.
Habileté : créer des suites croissantes et décroissantes
Avant de créer des suites, les élèves doivent d’abord reconnaître, comparer, décrire, changer la représentation et prolonger une grande variété de suites. Au départ, l’utilisation du matériel de manipulation est indispensable pour représenter les suites. En effet, au moment de la création de suites, les élèves peuvent facilement changer un élément du motif et en vérifier la régularité. Par contre, en dessinant une suite sur du papier, les élèves se concentrent sur le dessin à reproduire plutôt que sur la suite entière ou la nature de la régularité.
Voici un exemple dans lequel les élèves démontrent leur compréhension du concept de régularité en créant une suite et en l’expliquant.
Le personnel enseignant demande d’abord aux élèves de travailler en petits groupes afin de favoriser l’échange d’idées, et peut fournir les attributs et la structure de la suite ainsi que le matériel nécessaire pour la créer. Lors d’un échange mathématique, les présentations des suites permettent d’identifier les différentes représentations d’une même régularité et de vérifier la façon dont les élèves communiquent leur compréhension.
Le personnel enseignant demande ensuite aux élèves de créer une suite et de l’échanger avec une ou un partenaire. Il les invite à construire une représentation différente de la suite reçue, à décrire sa structure, à la prolonger ou à en produire une complètement différente aux fins de comparaison. Il faut cependant préciser aux élèves de limiter le nombre d’éléments dans le motif, car cela risque de rendre difficile l’identification de la structure de la suite.
Source : Guide d’enseignement efficace des mathématiques de la maternelle à la 3e année, p. 39-41.
Exemple
Donner une régularité d’addition ou de soustraction (par exemple, +23 ou -23). Demander aux élèves de créer différentes suites ayant cette régularité et de les comparer.
Source : Guide d’enseignement efficace des mathématiques de la maternelle à la 3e année, p. 63.
Habileté : représenter des suites et établir des liens entre les différentes représentations
L’habileté à communiquer un raisonnement algébrique se développe lorsque les élèves expriment leur compréhension d’une situation-problème ou d’un concept, et défendent leurs idées en utilisant différents modes de représentation :
- concret, lié à l’exploration, à la manipulation et à la création à l’aide de matériel concret;
- semi-concret, lié à une illustration, à un dessin ou à toute autre représentation sur papier;
- symbolique, lié à toute représentation faite à partir de chiffres ou de symboles;
- « en mots », lié à une explication ou à une description verbale ou écrite.
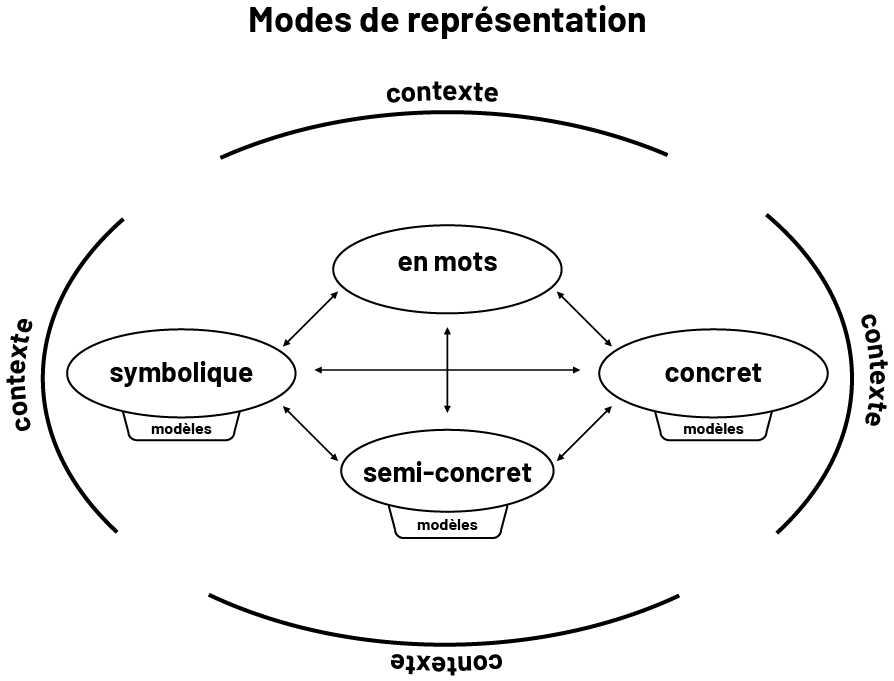
Source : Guide d’enseignement efficace des mathématiques de la 4e à la 6e année, p. 18.
Afin d’acquérir une solide compréhension, les élèves doivent vivre des expériences en contexte en explorant des situations-problèmes. La mise en contexte permet aux élèves d’établir des liens entre diverses représentations et de développer une compréhension des concepts algébriques explorés. Le personnel enseignant utilise aussi diverses représentations afin d’aider les élèves à s’approprier les concepts mathématiques et à établir des liens entre les représentations.
Au cycle moyen, les élèves explorent les relations et les représentent de différentes façons. En 4e et en 5e année, les élèves apprennent qu’une relation peut être représentée par une situation (suite non numérique), une table de valeurs ou une représentation graphique. Les flèches dans le schéma ci-dessous indiquent les liens entre les diverses représentations usuelles d’une relation.
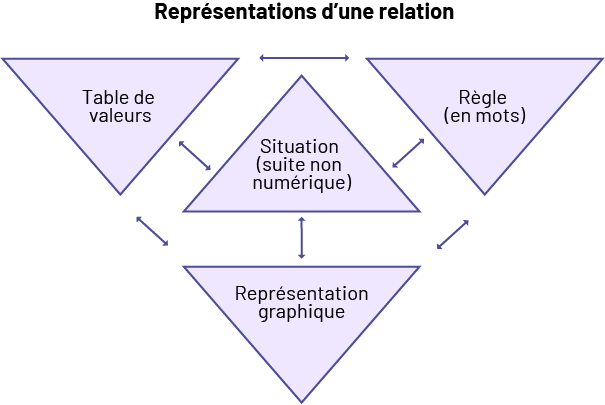
Source : Guide d’enseignement efficace des mathématiques de la 4e à la 6e année, p. 41.
L’utilisation de représentations multiples d’une même suite pour communiquer sa compréhension est une composante essentielle du développement de la pensée algébrique. Les suites non numériques et numériques croissantes et décroissantes peuvent être représentées sous différentes formes, soit à l’aide d’une description orale, d’une table de valeurs, de matériel concret et de représentations graphiques.
Description orale
Représenter une suite décroissante à l’aide de mots
Lorsqu’une suite numérique décroissante est présentée aux élèves, le personnel enseignant doit leur offrir différentes occasions de la représenter à l’aide de mots. Il s’agit d’une étape essentielle dans le cheminement des élèves pour les amener à déterminer l’expression algébrique de la suite.
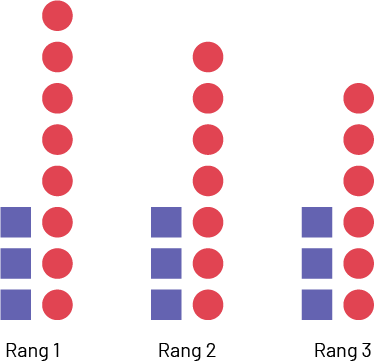
La suite non numérique à motif décroissant peut être décrite comme suit :
- La figure au rang 1 est composée de 3 carrés bleus et de 8 cercles rouges.
- La figure au rang 2 est composée de 3 carrés bleus et de 7 cercles rouges.
- La figure au rang 3 est composée de 3 carrés bleus et de 6 cercles rouges.
Les élèves peuvent aussi remarquer que le nombre de carrés bleus, soit 3, demeure constant, tandis que le nombre de cercles rouges diminue de 1.
Matériel de manipulation
Le matériel de manipulation (par exemple, carreaux algébriques, cubes emboîtables, jetons, réglettes Cuisenaire) est très varié. Son utilisation aide les élèves à explorer, à représenter et à faire des modifications facilement en cours d’essais. Voici des exemples d’utilisation de matériel de manipulation.
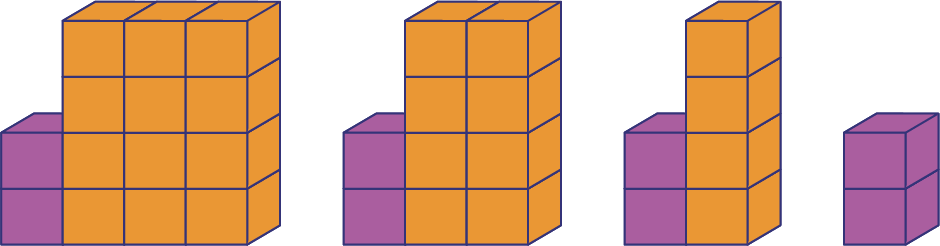
Représenter une suite décroissante à l’aide de matériel de manipulation
Demander aux élèves de représenter la suite numérique 14, 10, 6, 2 de façon concrète afin de rendre la régularité plus visible, et ce, en créant une suite décroissante à l’aide du matériel de manipulation de leur choix.
Questions pertinentes
- Combien de cubes (jetons, blocs…) utiliserez-vous pour représenter concrètement le terme de la suite au 1er rang? Au 2e rang? Au 3e rang? …
- Quel changement remarquez-vous d’un rang à l’autre?
- Qu’est-ce qui ne change pas d’un rang à l’autre (la constante)?
- Quelle est la règle de régularité? Comment le savez-vous?
Source : Guide d’enseignement efficace des mathématiques de la 4e à la 6e année, p. 212.
Illustration
L’illustration permet aux élèves de créer une représentation personnelle semi-concrète de leurs observations et de leur compréhension, ce qui les aide à clarifier leur pensée. Elle s’avère particulièrement avantageuse pour les élèves qui éprouvent de la difficulté à écrire ou à utiliser des symboles comme moyen de représentation, les dessins tenant lieu de justifications ou d’explications.
De nombreux types de problèmes incitent naturellement les élèves à réaliser un dessin pour les aider à les résoudre. Il arrive aussi que les élèves aient recours au matériel de manipulation en même temps. Or, plus les élèves acquièrent une pensée abstraite, plus les élèves délaissent le matériel de manipulation pour des dessins. Voici des exemples d’utilisation d’une illustration.
Représenter une suite croissante par une illustration
Présenter aux élèves la situation suivante :
| Semaine | 1 | 2 | 3 | 4 |
|---|---|---|---|---|
| Somme d'argent dans la tirelire | 5 | 9 | 13 | 17 |
Demander aux élèves d’illustrer la situation et de déterminer la somme d’argent que les parents lui donnent chaque semaine, et la somme accumulée de semaine en semaine.
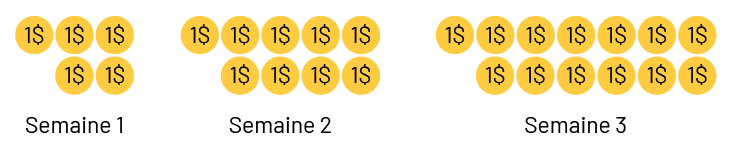
Questions pertinentes
- De quelle façon l’illustration aide-t-elle à déterminer la règle de régularité?
- Quelle somme d’argent Simon aura-t-il dans la tirelire la 5e semaine? Comment le savez-vous?
- Si Simon reçoit une même somme chaque semaine, comment expliquer qu’il a 5 $ après la 1re semaine?
- Comment pouvez-vous déterminer la somme dans la tirelire après un grand nombre de semaines, par exemple, la 10e semaine?
Source : Guide d’enseignement efficace des mathématiques de la 4e à la 6e année, p. 214-215.
Table de valeurs
La table de valeurs permet de représenter semi-concrètement la relation entre deux quantités changeantes (variables), dont l’une dépend de l’autre. La table de valeurs est souvent créée pour représenter la relation entre des valeurs numériques associées aux termes d’une suite non numérique croissante et le rang de ces termes.
La table de valeurs peut également être utilisée pour présenter des valeurs de variables d’une équation ou dans un contexte de résolution de problèmes.
Représenter une situation-problème à l’aide d’une table de valeurs
Dans un contexte de résolution de problèmes, les élèves peuvent aussi établir un lien entre une situation exprimée en mots et une table de valeurs.
Présenter la situation-problème suivante :
Pour mieux comprendre cette relation, les élèves peuvent la modéliser en utilisant du matériel concret ou semi-concret et des mots.

|
Lorsqu’on loue 1 film, il y a 4 $ d’abonnement et 1 x 5 $, donc on débourse 9$. Lorsqu’on loue 2 films, il y a 4 $ d’abonnement et 2 x 5 $, donc on débourse 14$. Lorsqu’on loue 3 films, il y a 4 $ d’abonnement et 3 x 5 $, donc on débourse 19$. Lorsqu’on loue 4 films, il y a 4 $ d’abonnement et 4 x 5 $, donc on débourse 24$. |
Par la suite, les élèves peuvent utiliser une table de valeurs pour représenter la relation entre le nombre de films loués et la somme déboursée.
| Nombre de films loués | Somme déboursée ($) |
|---|---|
| 1 | 9 |
| 2 | 14 |
| 3 | 19 |
| 4 | 24 |
| ... | ... |
Source : Guide d’enseignement efficace des mathématiques de la 4e à la 6e année, p. 51.
Représentation graphique d’une relation
Un diagramme permet de représenter de façon schématique un ensemble de données. Au cycle moyen, au domaine Données, les élèves apprennent notamment à représenter des données en utilisant différents diagrammes. Les élèves peuvent se servir de ces connaissances dans le domaine d’Algèbre. L’allure de l’ensemble des données dans un diagramme (par exemple, bandes en ordre croissant ou décroissant) permet une analyse du changement et facilite l’interpolation et l’extrapolation. La table de valeurs est utilisée pour créer le diagramme. Voici des exemples d’utilisation d’un diagramme.
Représenter la relation entre deux quantités changeantes (dans une table de valeurs) à l’aide d’une représentation graphique
Présenter la situation suivante :
| Nombre de pichets vendus | 1 | 2 | 3 |
|---|---|---|---|
| Somme perçue ($) | 4 | 8 | 12 |
Ensuite, présenter les données dans un diagramme comme celui-ci :

Source : Guide d’enseignement efficace des mathématiques de la 4e à la 6e année, p. 233.
Questions pertinentes
- Quels changements y a-t-il d’un pichet à l’autre en ce qui a trait à la vente? Ces changements sont-ils toujours les mêmes? Pourquoi?
- En examinant le diagramme, comment est-ce possible de déterminer la prochaine entrée d’argent?
- Quelle est la relation entre le nombre de pichets vendus et la somme perçue?
- Comment les trois premières valeurs représentées dans le diagramme peuvent-elles vous aider à déterminer la somme perçue après la vente de huit pichets?
Représenter la relation entre deux quantités changeantes (avec une illustration) à l’aide d’un diagramme à bandes
Présenter la situation suivante :
Avec les élèves, représenter les jardinets à l’aide d’une illustration.
Par exemple :

Au moyen d’une table de valeurs, représenter la relation entre le périmètre d’un jardinet et le nombre d’espaces carrés qu’il occupe.
| Nombre d’espaces carrés | Périmètre (m) |
|---|---|
| 1 | 4 |
| 2 | 6 |
| 3 | 8 |
Ensuite, représenter les données dans un diagramme comme celui-ci :
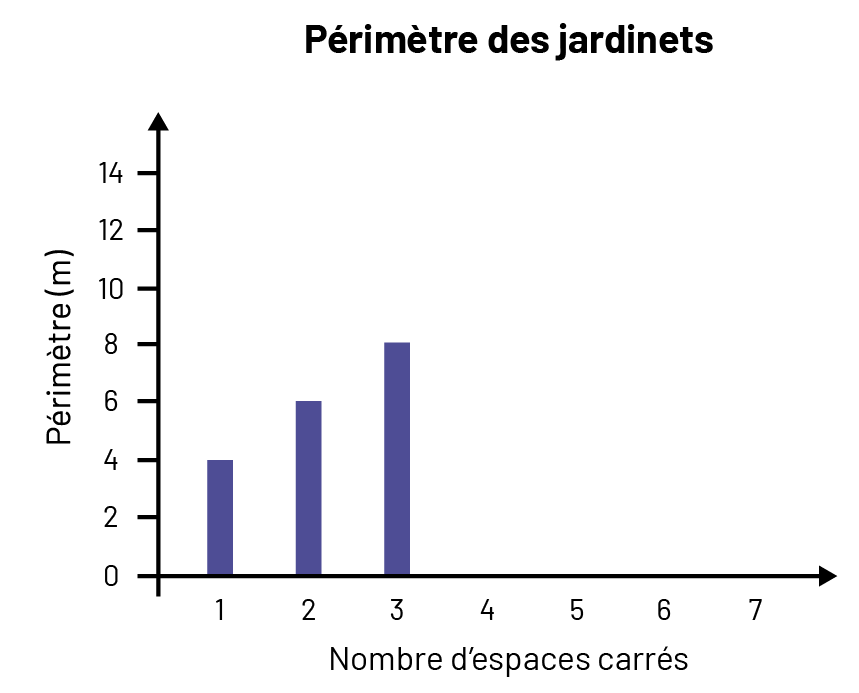
Questions pertinentes
- Quel changement y a-t-il entre les valeurs du nombre d’espaces carrés? Entre les valeurs des périmètres? Pourquoi?
- Quelles seraient les prochaines entrées dans la table de valeurs?
- Quelle est la relation entre le nombre d’espaces carrés et le périmètre d’un jardinet?
- Comment pourriez-vous utiliser le diagramme pour déterminer le périmètre d’un jardinet de 8 espaces carrés?
Source : Guide d’enseignement efficace des mathématiques de la 4e à la 6e année, p. 234-235.
Connaissance : table de valeurs
La table de valeurs permet de représenter semi-concrètement la relation entre deux quantités changeantes (variables), dont l’une dépend de l’autre. À la fin du cycle primaire, les élèves ont appris à créer des tables de valeurs pour représenter des relations dans des situations-problèmes.
La table de valeurs est souvent créée pour représenter la relation entre des valeurs numériques associées aux termes d’une suite non numérique à motif croissant et le rang de ces termes.
Exemple
On peut étudier la relation entre le rang d’une figure dans une suite non numérique et le nombre d’objets qui le composent. Le rang de la figure est inscrit dans la première colonne (ou rangée) et le nombre d’objets qui composent le rang (valeur du terme) est inscrit dans la deuxième colonne (ou rangée). La régularité des termes de la deuxième colonne (ou rangée) peut être utilisée pour prolonger la table de valeurs.
Table de valeurs à la verticale
| Rang de la figure | Nombre d’objets |
|---|---|
| 1 | 2 |
| 2 | 4 |
| 3 | 6 |
| 4 | … |
Table de valeurs à l’horizontale
| Rang de la figure | 1 | 2 | 3 |
|---|---|---|---|
| Nombre d’objets | 2 | 4 | 6 |
La table de valeurs peut être disposée verticalement ou horizontalement et séparée en colonnes ou en rangées. Il est bon de varier la présentation de la table de valeurs afin que les élèves s’habituent aux deux dispositions.
Source : Guide d’enseignement efficace des mathématiques de la 4e à la 6e année, p. 231.
Connaissance : représentation graphique
Les suites à motif croissant peuvent servir d’introduction aux représentations graphiques. Le rang des figures dans les suites à motif croissant correspond aux valeurs sur l’axe horizontal. Le nombre total d’éléments de chaque figure est représenté par les valeurs sur l’axe vertical. L’axe vertical représente aussi le nombre d’éléments qu’il y aura au rang 0 (la valeur de la constante), qui est l’ordonnée de la représentation graphique.
Source : Guide d’enseignement efficace des mathématiques de la 7e à la 10e année, p. 63.
Exemple
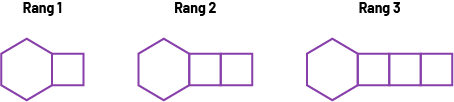
Relation entre le rang et le nombre de cure-dents
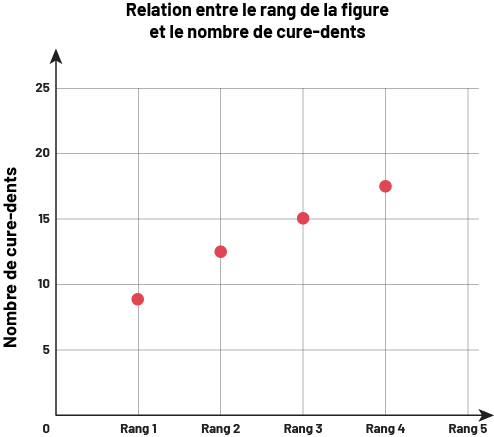
Source : En avant, les maths!, 6e année, CM, Algèbre, p. 5-6.
