C2.1 Translate among words, algebraic expressions, and visual representations that describe equivalent relationships.
Skill: describe equivalence relationships using words, algebraic expressions and visual representations
"Communication benefits everyone involved in the exchange […]. The obligation to share one's understanding of a situation or concept often contributes to the improvement or deepening of that understanding."
(Ministère de l'Éducation du Québec, 2001, p. 132)
The ability to communicate algebraic reasoning is developed when students express their understanding of a problem situation or concept and defend their ideas using different representations:
- concrete, related to exploration, manipulation and creation using concrete materials;
- semi-concrete, related to an illustration, drawing or other representation on paper;
- symbolic, linked to any representation made from numbers or symbols;
- "in words", linked to a verbal or written explanation or description.
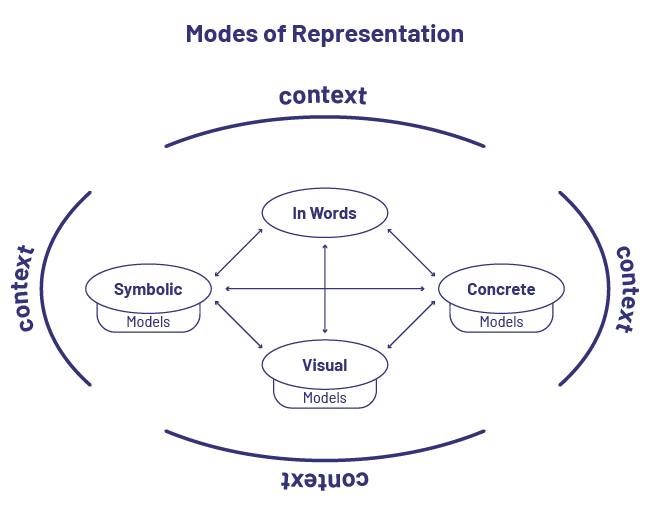
In order to develop a solid understanding, students need to have experiences in context by exploring problem situations. Contextualization allows students to make connections between various representations and develop an understanding of the algebraic concepts being explored. Teachers also use a variety of representations to help students take ownership of mathematical concepts and make connections between representations.
Source : Guide d’enseignement efficace des mathématiques de la 4e à la 6e année, p. 17-18.
Symbolic reasoning allows for the interpretation of various mathematical relationships and the representation of algebraic reasoning.
"Even before beginning the study of algebra, students must learn to use symbols as elements of a language by which to express ideas. In this way, algebra will no longer be a series of meaningless rules and procedures." (Lodholz, 1990, p. 29)
Algebra is used to understand and establish mathematical relationships and to communicate ideas. To this end, symbols have an important place in algebra. When students are able to represent a mathematical situation, relationship, or idea using symbols, they demonstrate a level of abstraction that demonstrates algebraic reasoning.
Symbol sense is to algebra what number sense is to arithmetic. Recently introduced into the discourse of mathematics teaching and learning (Bergsten, 1999, p. 123), symbol sense is essential to success in algebra.
Symbolic reasoning involves :
- understanding when and how to use symbols to communicate;
- describing relationships in a symbolic way;
- recognizing that symbols can be used to help solve problems;
- reading and interpreting mathematical sentences accurately and meaningfully;
- treating the "=" sign as the expression of the equality relationship between two quantities;
- interpreting the value of variables;
- represent the properties of numbers and operations algebraically (for example, the equality a + b = b + a represents the commutativity of addition);
- working in an abstract context.
Continued exploration of the use of symbols in a variety of mathematical contexts allows students to make sense of those symbols (Small, 2005, p. 73).
Early in the primary grades, students begin to develop a sense of symbols (e.g., understanding and writing the numbers from 0 to 9 and the operations signs). Students learn to represent situations involving equality concretely (e.g., using cubes) and semi-concretely (e.g., using drawings), and then using personal symbols (e.g., using a sun to represent a missing quantity).
In the junior grades, students continue to use symbols and to develop a sense of ownership of them. In particular,
students gradually replace personal symbols with literal symbols to represent variables (for example, 13 + a
= 19). They also use symbols to communicate algebraic reasoning.
Source : Guide d’enseignement efficace des mathématiques de la 4e à la 6e année, p. 67-69.
In order to develop a thorough understanding of the use of the symbol, it is important that students be able to represent formulas and relationships using a variety of models. In grade 5, understanding of the symbol is demonstrated through its representation visually, using words, and using algebraic expressions.
Knowledge: Equivalence Relationship
Relationship between two equal quantities.
Equality is represented by the sign "=" (is equal to).
Notes
- The teacher may, for instructional purposes, write a false equality such as "3 + 3 = 4 + 1" and have students check it and then correct it to represent a true statement.
- The expression to the left of the "=" sign is the left-hand side of the equality and the expression to the right is the right-hand side of the equality.
Example
4 plus 5 equal 8 plus one. ‘’a’’ equals 4 plus 2.3 plus 3 equals 4 plus one. It is a false equality.3 plus 3 equals one plus 5. It is a true equality.2 plus 3 equals one plus 42 plus 3 on the left side and 4 on the right side.
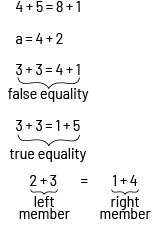
Source : Guide d’enseignement efficace des mathématiques de la 4e à la 6e année, p. 69.
Knowledge: algebraic expression
An expression is a numeric or algebraic representation of a quantity. An expression may include numbers, variables, and operations. Specifically, an expression such as 3 + n + 4 is an algebraic expression, since it contains numbers and symbols.
Notes
- An expression containing only numbers is a numeric expression, for example 5 - 2.