C2.1 Décrire des relations d’équivalence à l’aide de mots, d’expressions algébriques et de représentations visuelles, et établir les liens entre les représentations.
Habileté : décrire des relations d’équivalence à l’aide de mots, d’expressions algébriques et de représentations visuelles
« La communication bénéficie à tous ceux qui participent à l’échange […]. L’obligation de faire part de sa compréhension d’une situation ou d’un concept contribue souvent à l’amélioration ou à l’approfondissement de cette compréhension. »
(Ministère de l’Éducation du Québec, 2001, p. 132)
L’habileté à communiquer un raisonnement algébrique se développe lorsque les élèves expriment leur compréhension d’une situation-problème ou d’un concept, et défendent leurs idées en utilisant différents modes de représentation :
- le mode concret, lié à l’exploration, à la manipulation et à la création à l’aide de matériel concret;
- le mode semi-concret, lié à une illustration, à un dessin ou à toute autre représentation sur papier;
- le mode symbolique, lié à toute représentation faite à partir de chiffres ou de symboles;
- le mode « en mots », lié à une explication ou à une description verbale ou écrite.
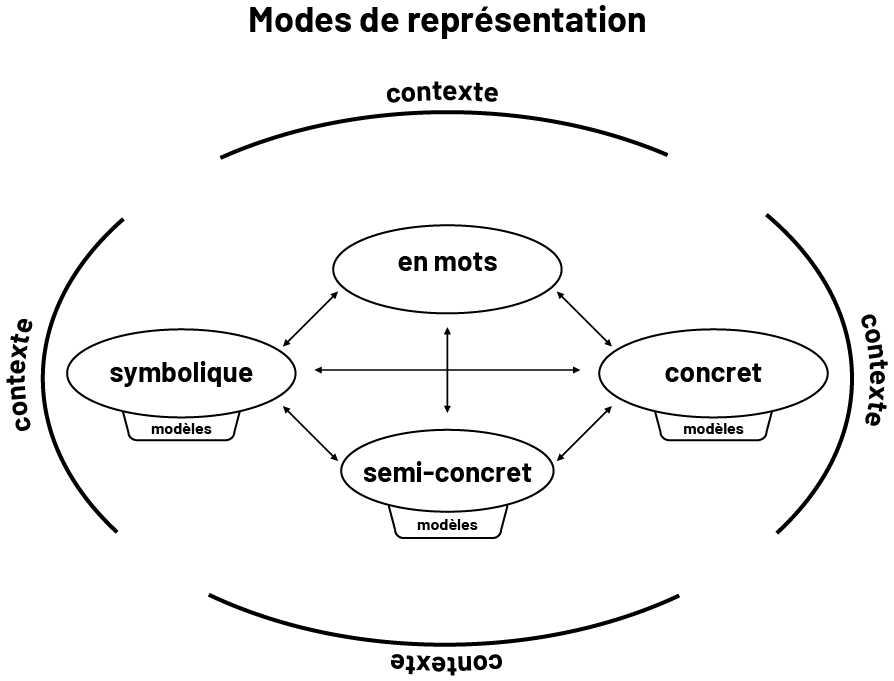
Afin d’acquérir une solide compréhension, les élèves doivent vivre des expériences en contexte en explorant des situations-problèmes. La mise en contexte permet aux élèves d’établir des liens entre diverses représentations et de développer une compréhension des concepts algébriques explorés. Le personnel enseignant utilise aussi diverses représentations afin d’aider les élèves à s’approprier les concepts mathématiques et à établir des liens entre les représentations.
Source : Guide d’enseignement efficace des mathématiques de la 4e à la 6e année, p. 17-18.
Le sens du symbole permet d’interpréter diverses relations mathématiques et de représenter un raisonnement algébrique.
« Avant même de commencer l’étude de l’algèbre, les élèves doivent apprendre à utiliser les symboles comme éléments d’un langage par lequel on exprime des idées. Ainsi, l’algèbre ne sera plus une série de règles et de procédures vides de sens. » [traduction libre] (Lodholz, 1990, p. 29)
L’algèbre est utilisée pour comprendre et établir des relations mathématiques et pour communiquer des idées. À cette fin, les symboles ont une place importante en algèbre. Lorsque les élèves sont en mesure de représenter une situation, une relation ou une idée mathématique à l’aide de symboles, elles et ils font preuve d’un niveau d’abstraction qui démontre un raisonnement algébrique.
Le sens du symbole est à l’algèbre ce que le sens du nombre est à l’arithmétique. Introduit récemment dans le discours sur l’enseignement et l’apprentissage des mathématiques (Bergsten, 1999, p. 123), le sens du symbole est essentiel à la réussite en algèbre.
Avoir le sens du symbole, c’est être en mesure :
- de comprendre quand et comment utiliser des symboles pour communiquer;
- de décrire des relations de façon symbolique;
- de reconnaître que les symboles peuvent faciliter la résolution de problèmes;
- de lire et d’interpréter des phrases mathématiques de façon juste et signifiante;
- de traiter le signe « = » comme l’expression d’une égalité entre deux quantités;
- d’interpréter la valeur des variables;
- de représenter les propriétés des nombres et des opérations de façon algébrique (par exemple, l’égalité a + b = b + a représente la commutativité de l’addition);
- de travailler dans un contexte abstrait.
L’exploration continue de l’utilisation de symboles dans des contextes mathématiques variés permet aux élèves de donner un sens à ces symboles (Small, 2005, p. 73).
Très tôt au cycle primaire, les élèves commencent à développer le sens du symbole (par exemple, avec la compréhension et l’écriture des chiffres de 0 à 9 et des signes d’opération). Les élèves apprennent à représenter des situations d’égalité de façon concrète (par exemple, à l’aide de cubes) et semi-concrète (par exemple, à l’aide d’illustrations), puis à l’aide de symboles personnels (par exemple, en utilisant un soleil pour représenter une quantité manquante).
Au cycle moyen, les élèves continuent à utiliser les symboles et à s’en approprier le sens. Notamment, les élèves remplacent progressivement les symboles personnels par des symboles littéraux pour représenter des variables (par exemple, 13 + a = 19). Elles et ils utilisent aussi les symboles pour communiquer un raisonnement algébrique.
Source : Guide d’enseignement efficace des mathématiques de la 4e à la 6e année, p. 67-69.
Afin de développer une compréhension approfondie de l’utilisation du symbole, il importe que l’élève puisse représenter des formules et des relations au moyen de divers modèles. En 5e année, la compréhension du symbole est démontrée par sa représentation de façon visuelle, à l’aide de mots et à l’aide d’expressions algébriques.
Connaissance : relation d’équivalence
Relation entre deux quantités égales.
L’égalité est représentée par le signe « = » (est égal à).
Notes
- L’enseignante ou l’enseignant peut, pour des raisons pédagogiques, écrire une égalité fausse comme « 3 + 3 = 4 + 1 » et demander aux élèves de la vérifier, puis de la corriger afin de représenter une égalité vraie.
- L’expression à la gauche du signe « = » est le membre de gauche de l’égalité et l’expression à la droite est le membre de droite de l’égalité.
Exemple

Source : Guide d’enseignement efficace des mathématiques de la 4e à la 6e année, p. 69.
Connaissance : expression algébrique
Une expression est un symbole ou un ensemble de symboles qui peuvent être reliés entre eux à l’aide d’un signe d’opération. Plus précisément, une expression comme 3 + n + 4 est une expression algébrique, puisqu’elle contient des nombres et des symboles.
Une expression contenant exclusivement des nombres est une expression numérique, par exemple 5 – 2.
Source : Curriculum de l’Ontario. Programme-cadre de mathématiques de la 1re à la 8e année, 2020, Ministère de l’Éducation de l’Ontario.
