C1.4 Create and describe patterns to illustrate relationships among whole numbers and decimal tenths and hundredths
Activity 1: Counting in Chorus
From a young age, students skip count by 1, 2, 5, 10. 25, etc. Skip counting and writing the count as a sequence of numbers can help students notice the relationships between numbers. It is important to continue to have students skip count in the junior grades with different types of numbers, such as large whole numbers (for example, skip counting by 5,000. 25,000), fractions (for example, skip counting by "one-third" by saying 1 one-third, 2 one-third, 3 one-third, 1, etc.), and so on, up to at least 5, and decimal numbers (tenths or hundredths). The way numbers are written when students recite them is intentional and should be planned to show relationships.
Prerequisite
Before having students count in "two-tenths" increments, have students count in "one-tenth" increments.
Materials
- whiteboard or chart paper
- felt-tip pens
- number line 0 to 5 divided into tenths or 10 frames (explain that for the activity each frame is considered 1 whole)
Directions
- As a whole class share with the students that they are going to count together in "2 tenths" increments from 0 to 5. First, give the students a minute to think about the numbers that will be recited. Then, begin counting all together at a pace that allows you to write the numbers. You can also show the visual on the number line or on the 10 frames.
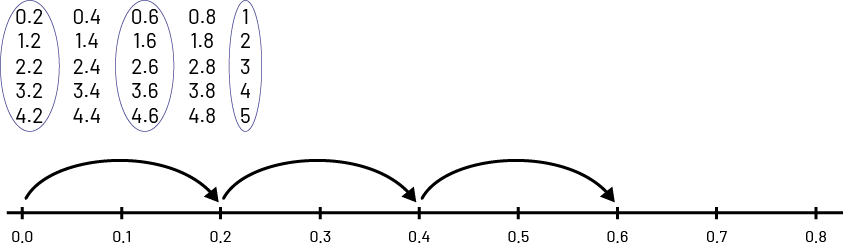
- As students recite the numbers, write them down like this: 0.2 0.4 0.6 0.8 (two-tenths, four-tenths, six-tenths, eight-tenths).
- Pause here and ask students to think of the next number. Ask them how they will pronounce it and how it will be written.
- Conduct a Think-Pair-Share.
- Note that a number of students will think that the next number will be written 0.10.
- As you pronounce 10 tenths \(\frac{10}{10}\), write 1. Ask students why it is spelled that way. So, 10 tenths is ONE. This is best illustrated on the number line or with a filled-in 10 frame.
0.2 0.4 0.6 0.8 1
Continue to 5, writing the numbers in this way to highlight the relationships between them.
0.2 0.4 0.6 0.8 1
1.2 1.4 1.6 1.8 2
2.2 2.4 2.6 2.8 3
3.2 3.4 3.6 3.8 4
4.2 4.4 4.6 4.8 5
Ask students to observe the written numbers after counting in two-tenths increments to 5.
Ask them what they notice about numbers by conducting a Think-Pair-Share.
Point out the relationships between the numbers they observed. Here are some examples:
Suggestion
Use this opportunity to make the connection with fractions. For each decimal number recited, you can also write a fraction. For example, 0.2 can be written as 2/10. Highlight to students that decimal numbers in tenths can also be written as fractions with a denominator of 10. Both represent the same value.
Similarly, if you are counting in hundredths, take the opportunity to make the connection between decimal numbers and fractions with 100 as the denominator. For example, it is possible to write 25 hundredths as 0.25 or 25/100.
Activity 2: Relationships in Decimal Numbers
Present the following situation to students:
a) How does Miray's patterns show the relationships between ones, tenths, and hundredths?
| 4.63 |
|---|
| 4 ones + 6 tenths + 3 hundredths |
| 4 ones + 5 tenths + 13 hundredths |
| 4 ones + 4 tenths + 23 hundredths |
| 4 ones + 3 tenths + 33 hundredths |
| 4 ones + 2 tenths + 43 hundredths |
| 4 ones + 1 tenth + 53 hundredths |
| 4 ones + 0 tenth + 63 hundredths |
| 4.63 |
|---|
| 4 ones + 6 tenths + 3 hundredths |
| 3 ones + 16 tenths + 3 hundredths |
| 2 ones + 26 tenths + 3 hundredths |
| 1 one + 36 tenths + 3 hundredths |
| 0 one + 46 tenths + 3 hundredths |
Strategy 1
Describing Patterns Verbally
- In this pattern, I notice that as the tenths decrease by 1, the hundredths increase by 10. In each tenth, there are 10 hundredths.
- In this pattern, I notice that as the ones decrease by 1, the tenths increase by 10. In each one, there are 10 tenths.
Strategy 2
Describing a Pattern Using Base 10 Material
- I represent the first 4 equalities in the 1st set of related operations using base 10 material. In each tenth, there are 10 hundredths. I notice that as the tenths decrease by 1, the hundredths increase by 10.
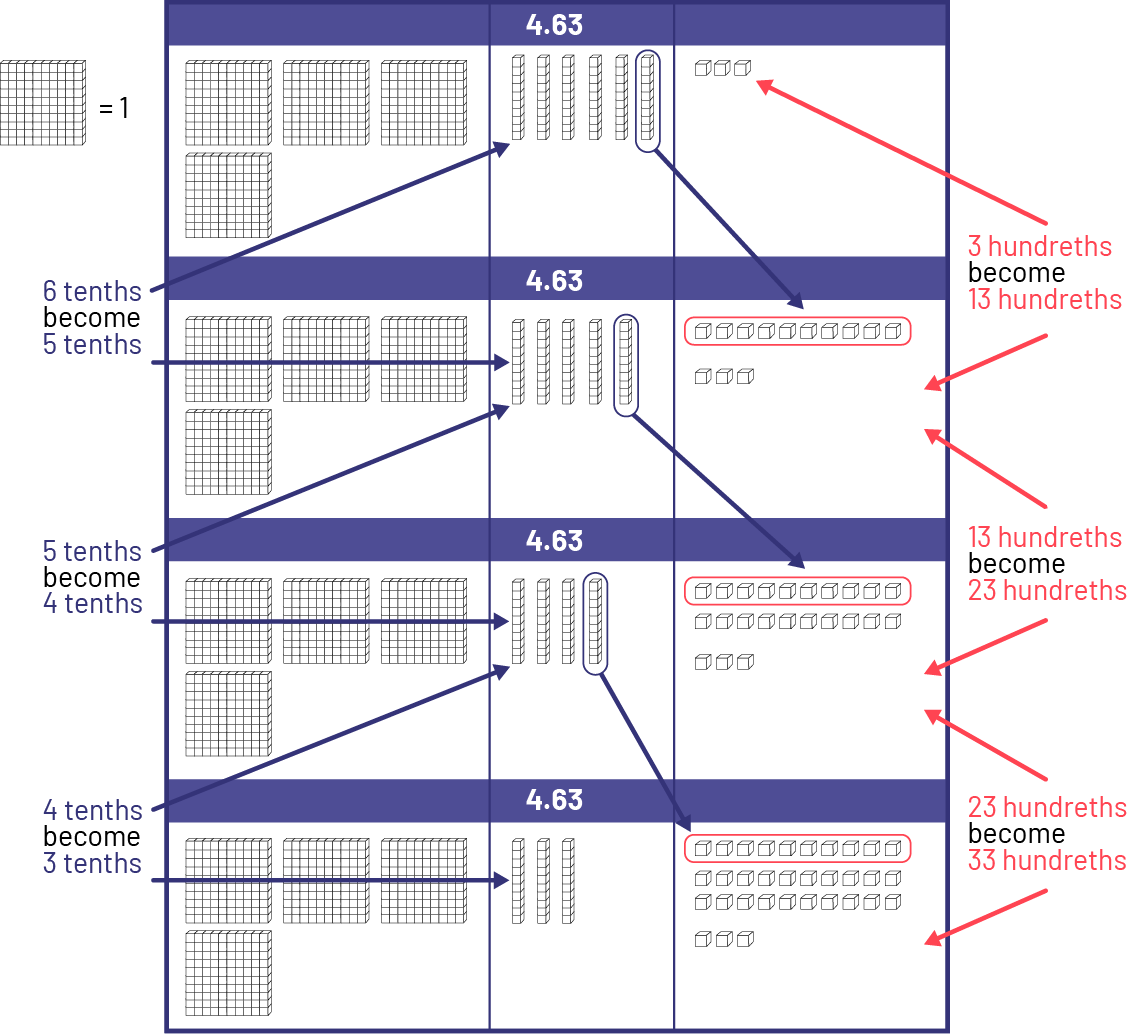
- I represent equalities in the 2nd set of related operations using base 10 material. In each unit, there are 10 tenths. I notice that as the units decrease by 1, the tenths increase by 10.

b) Create a set of related addition operations and a set of related subtraction operations using the number 4.63.
c) Miray wonders if there are any patterns in the multiplication and division tables. Create a numeric pattern to show the relationship between multiplication and division facts for a number of your choice.
Source: translated from En avant, les maths!, 5e année, CM, Algèbre, Habiletés liées aux relations dans les suites p. 9-13.
