C1.4 Créer et décrire des suites numériques comprenant des nombres naturels, des nombres décimaux jusqu’aux dixièmes et des nombres décimaux jusqu’aux centièmes, et représenter des relations entre les nombres.
Activité 1 : compter en chorale
Depuis un jeune âge, les élèves comptent, soit par bonds de 1, de 2, de 5, de 10, de 25, etc. Le fait de compter par bonds et d’écrire la suite numérique qui en découle, amène les élèves à voir les relations entre les nombres. Il est important de continuer à faire compter les élèves au cycle moyen avec différents types de nombres, tels que de grands nombres naturels (par exemple, compter par bonds de 5 000, de 25 000), des fractions (par exemple, compter par bonds de « un tiers » en disant 1 un tiers (\(\frac{1}{3}\)), 2 un tiers (\(\frac{2}{3}\)), 3 un tiers (\(\frac{3}{3}\) 1 tout), etc., jusqu’à au moins 5) et des nombres décimaux (dixièmes ou centièmes). La façon d’écrire les nombres lorsque les élèves les récitent est intentionnelle et doit être planifiée afin de faire ressortir des relations.
Préalable
Avant de faire compter les élèves par bonds de « deux dixièmes », animer une minileçon en comptant par bonds de « un dixième ».
Matériel
- tableau blanc ou papier grand format
- stylos-feutres
- droite numérique 0 à 5 sectionnée en dixièmes ou cadres à 10 cases (expliquer que, pour l’activité, chaque cadre est considéré comme 1 tout)
Démarche
Rassembler les élèves et leur dire qu’elles et ils vont compter ensemble par bonds de « 2 dixièmes » à partir de 0 jusqu’à 5. Allouer d’abord une minute aux élèves pour qu’elles et ils réfléchissent aux nombres qui seront récités. Ensuite, commencer à compter en choeur à un rythme qui vous permet d’écrire les nombres. Vous pouvez également montrer le visuel sur la droite numérique ou sur les cadres à 10 cases.
Au fur et à mesure que les élèves récitent les nombres, les écrire comme ceci : 0,2 0,4 0,6 0,8 (deux dixièmes, quatre dixièmes, six dixièmes, huit dixièmes).
Faire une pause ici et demander aux élèves de réfléchir au prochain nombre. Leur demander comment elles et ils vont le prononcer et comment il va s’écrire.
Faire un PPP (pense-parle-partage).
Noter qu’un certain nombre d’élèves vont penser que le prochain nombre s’écrira 0,10.
En prononçant 10 dixièmes (\(\frac{10}{10}\)), écrire 1. Demander aux élèves la raison pour laquelle il s’écrit ainsi. Donc, 10 dixièmes est UN TOUT. Cela s’illustre bien sur la droite numérique ou avec un cadre à 10 cases rempli.
Continuer jusqu’à 5 en écrivant les nombres de cette façon afin de faire ressortir les relations entre eux.
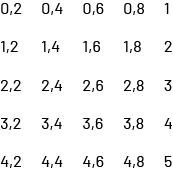
Demander aux élèves d’observer les nombres écrits après avoir compté par bonds de deux dixièmes jusqu’à 5.
Leur demander ce qu’elles et ils remarquent au sujet des nombres en faisant un PPP (pense-parle-partage).
Faire ressortir les relations entre les nombres qu’elles et ils ont observées. En voici quelques exemples :
image Suite de chiffres qui commencent à zéro virgule 2 et qui continue jusqu’à 5 en bonds de plus zéro virgule 2. Les chiffres sont placés sur 5 colonnes, toutes les virgules 2 sont placées ensemble et sont encerclées. Toutes les virgules 6 sont placées ensemble et sont encerclées. Tous les chiffres entiers sont placés ensemble et sont encerclés.Une bande numérique de zéro virgule zéro à zéro virgule 8. Des flèches représentent les bonds de plus zéro virgule 2.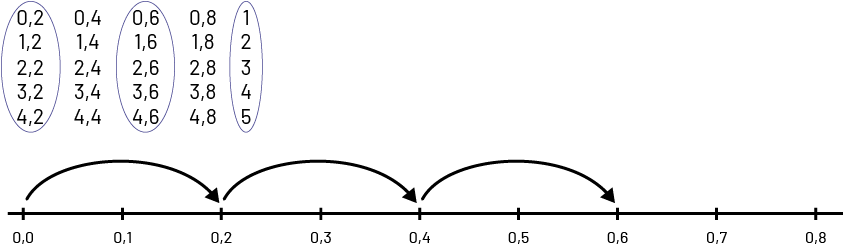
Suggestion
Profiter de l’occasion pour faire le lien avec les fractions. Pour chaque nombre décimal récité, on peut aussi écrire une fraction. Par exemple 0,2 ou \(\frac{2}{10}\). Amener les élèves à comprendre que les nombres décimaux en dixièmes peuvent être aussi écrits en fractions dont le dénominateur est 10. Les deux représentent la même quantité.
De même, si vous comptez en centièmes, profiter de l’occasion pour faire le lien entre les nombres décimaux et les fractions dont 100 est le dénominateur. Il est possible, par exemple, d’écrire 25 centièmes comme 0,25 ou \(\frac{25}{100}\).
Activité 2 : relations dans les nombres décimaux
Présenter la situation suivante aux élèves :
a) Décris les suites créées par Miray en représentant la relation entre les nombres dans les opérations apparentées
| 4.63 |
|---|
| 4 unités + 6 dixièmes + 3 centièmes |
| 4 unités + 5 dixièmes + 13 centièmes |
| 4 unités + 4 dixièmes + 23 centièmes |
| 4 unités + 3 dixièmes + 33 centièmes |
| 4 unités + 2 dixièmes + 43 centièmes |
| 4 unités + 1 dixième + 53 centièmes |
| 4 unités + 0 dixième + 63 centièmes |
| 4.63 |
|---|
| 4 unités + 6 dixièmes + 3 centièmes |
| 3 unités + 16 dixièmes + 3 centièmes |
| 2 unités + 26 dixièmes + 3 centièmes |
| 1 unité + 36 dixièmes + 3 centièmes |
| 0 unité + 46 dixièmes + 3 centièmes |
Stratégie 1
Description des suites à l’aide de mots
- Dans cette suite, je remarque que lorsque les dixièmes diminuent de 1, les centièmes augmentent de 10. Dans chaque dixième, il y a 10 centièmes.
- Dans cette suite, je remarque que lorsque les unités diminuent de 1, les dixièmes augmentent de 10. Dans chaque unité, il y a 10 dixièmes.
Stratégie 2
Description d’une suite à l’aide du matériel de base 10
- Je représente les 4 premières égalités dans la 1re série d’opérations apparentées à l’aide du matériel de base 10. Dans chaque dixième, il y a 10 centièmes. Je remarque que lorsque les dixièmes diminuent de 1, les centièmes augmentent de 10.
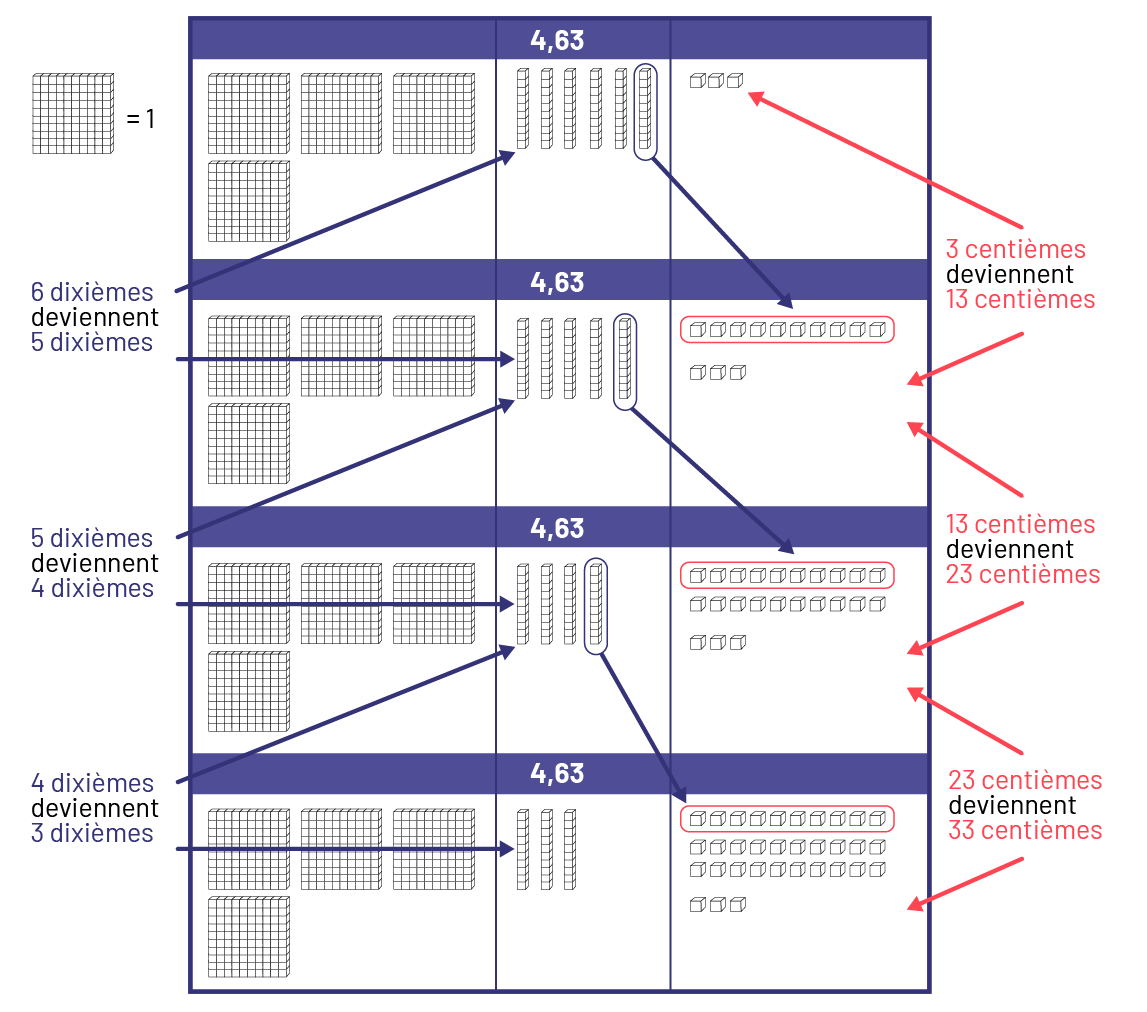 image Une
représentation qui nous montre des blocs de centaines, des bâtons de dizaine et des cubes de, une unité.Il est
mentionné que dans la démarche représentée;Un bloc centaine est égal à un.;6 dixièmes deviennent 5 dixièmes.;5
dixièmes deviennent 4 dixièmes.;4 dixièmes deviennent 3 dixièmes.;3 centièmes deviennent 13 centièmes.;13 centièmes
deviennent 23 centièmes.;23 centièmes deviennent 33 centièmes.
image Une
représentation qui nous montre des blocs de centaines, des bâtons de dizaine et des cubes de, une unité.Il est
mentionné que dans la démarche représentée;Un bloc centaine est égal à un.;6 dixièmes deviennent 5 dixièmes.;5
dixièmes deviennent 4 dixièmes.;4 dixièmes deviennent 3 dixièmes.;3 centièmes deviennent 13 centièmes.;13 centièmes
deviennent 23 centièmes.;23 centièmes deviennent 33 centièmes.
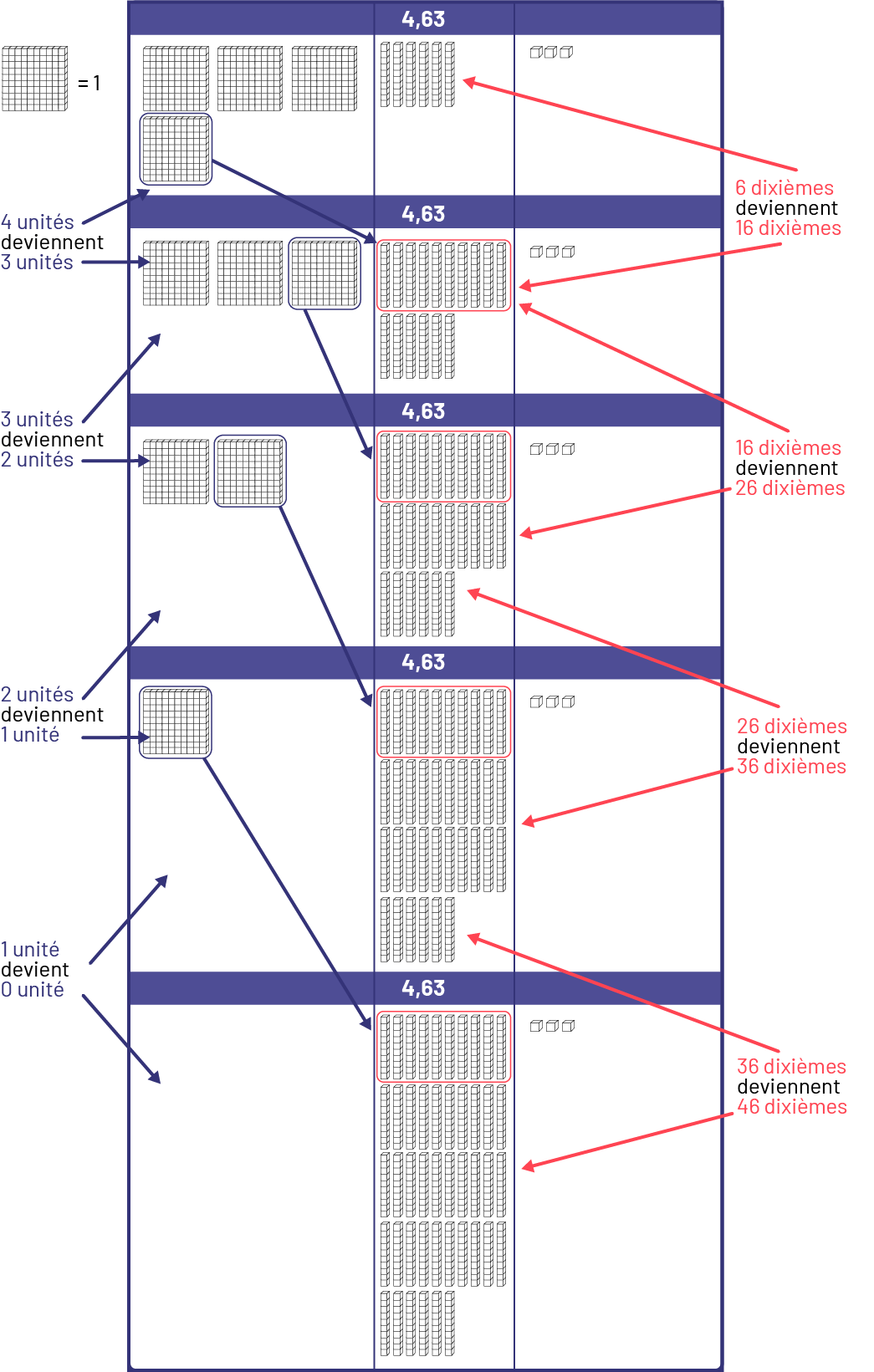
- Je représente les égalités dans la 2e série d’opérations apparentées à l’aide du matériel de base 10. Dans chaque unité, il y a 10 dixièmes. Je remarque que lorsque les unités diminuent de 1, les dixièmes augmentent de 10.
b) Crée une série d’opérations apparentées d’addition et une série d’opérations apparentées de soustraction comprenant le nombre 4,63.
c) Miray se demande s’il y a des régularités dans les tables de multiplication et de division. Crée une série d’opérations apparentée de multiplication et de division d’un produit de ton choix.
Source : En avant, les maths!, 5e année, CM, Algèbre, p. 9-13.
