C2.1 Translate among words, algebraic expressions, and visual representations that describe equivalent relationships.
Activity 1: Find the area of the triangle
Present the triangle below to the students.
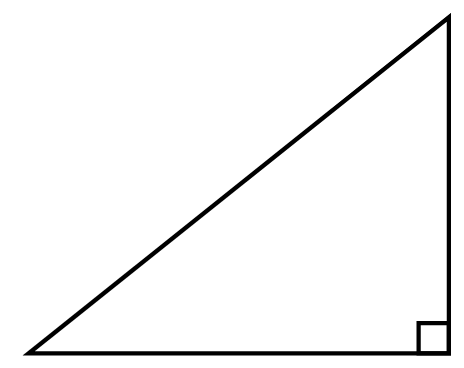
Ask students to describe the equivalence relationships using words and an algebraic expression to calculate the area of the triangle.
Ask questions such as:
- What algebraic expressions could be written to represent the area of this triangle? Justify your answer.
- How could algebraic expressions be described using words?
- What are the connections between the algebraic expressions found, the triangle shown, and the word representation of the formula? Explain your reasoning.
Have students observe that when a variable is multiplied by a number, it can be written without a space, such as bh.
Activity 2: Describe equivalence relationships
Read the statement below:
Ask students to represent this statement using an algebraic expression and a visual representation. Have students compare their representations to make connections between them.
Then invite students to take turns proposing a representation to the class (in words, as a visual representation or as an algebraic expression). The other students must then represent it in other ways. Pool the different representations.
Activity 3: Symbolic representation
Using a copy of Appendix 6.4 (Symbolic Representation of the First Puzzle) posted on the TBI, review the representation from an unknown of the first number puzzle. With student input, determine the algebraic expression that describes each step of the puzzle. Clarify that the letter(n in the example below) replaces the circle to represent the unknown and that this symbol can mean any starting number.
Example
Table that represents: step, representation from the unknown value, and symbolic representation.Step, add value of 6, unknwon and 6 sticks, ‘n’ plus 6.Step, substact value of 3, unkown and 3 sticks, ‘n’, plus 3. Step, add 5, unkown and 10 sticks, ‘n’ plus ten. Step, substact ten, unknown, ‘n’.
Divide students into teams of two and provide each team with a copy of Appendix 6.5 (Symbolic representation of the second puzzle). Ask students to write an algebraic expression corresponding to the results of each step in the second puzzle.
Example
Table that represents: step, representation from the unknown value, and symbolic representation.Step, choose a number, one to 5, unkonown, ’n’. Step, double the number, 2 unknown, 2 multiplied by “”.Step, add 6, 2 unknowns and 6 sticks, 2 multiplied by ‘n’ plus 6.Step, double the sum, 4 unknowns and 12 sticks, 4 multiplied by ‘n’ plus 12.Step, subtract 4, 4 unknowns and 8 sticks, 4 multiplied by ‘n’ plus 8. Step, divide by 4, one unknown and 2 sticks, 2 plus ‘n’. Step, subtract 2, one unknown, ‘n’.
Lead a discussion about different algebraic expressions, recognizing the possibility of having multiple equivalent algebraic expressions for the same step.
Source: A Guide to Effective Instruction in Mathematics, Grades 4 to 6, pp. 184-185.