C2.1 Décrire des relations d’équivalence à l’aide de mots, d’expressions algébriques et de représentations visuelles, et établir les liens entre les représentations.
Activité 1 : trouver l’aire du triangle
Présenter le triangle ci-dessous aux élèves.
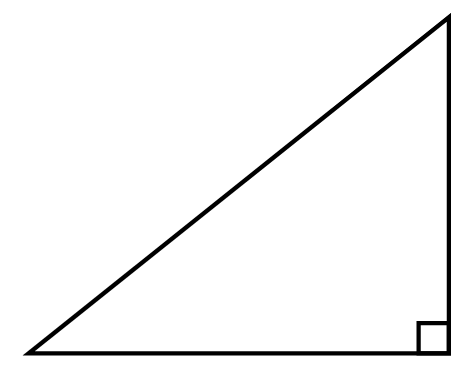
Demander aux élèves de décrire les relations d’équivalence à l’aide de mots et d’une expression algébrique afin de calculer l’aire du triangle.
Poser des questions telles que :
- Quelles expressions algébriques pourrait-on écrire pour représenter l’aire de ce triangle? Justifie ta réponse.
- À l’aide de mots, comment pourrait-on décrire les expressions algébriques?
- Quels sont les liens entre les expressions algébriques trouvées, le triangle illustré ainsi que la représentation de la formule à l’aide de mots? Explique ton raisonnement.
Faire observer aux élèves que, lorsqu’une variable est multipliée par un nombre, il est possible de l’écrire sans espace, comme bh.
Activité 2 : décrire des relations d’équivalence
Lire l’énoncé ci-dessous :
Demander aux élèves de représenter cet énoncé à l’aide d’une expression algébrique et d’une représentation visuelle. Inviter les élèves à comparer leurs représentations afin d’établir des liens entre elles.
Inviter ensuite les élèves à proposer, à tour de rôle, une représentation aux élèves de la classe (en mots, sous la forme d’une représentation visuelle ou d’une expression algébrique). Les autres élèves devront alors la représenter sous ses autres formes. Faire une mise en commun des différentes représentations.
Activité 3 : la représentation symbolique
À l’aide d’une copie de l’annexe 6.4 (Représentation symbolique de la première énigme) affichée au TBI, revoir la représentation à partir la valeur inconnue de la première énigme de nombres. Avec la participation des élèves, déterminer l’expression algébrique qui décrit chaque étape de l’énigme. Leur préciser que la lettre (n dans l’exemple ci-dessous) remplace le cercle pour représenter la valeur inconnue et que ce symbole peut signifier n’importe quel nombre de départ.
Exemple
image Tableau qui représente l’étape, la représentation à partir de la valeur inconnue et la représentation symbolique.Étape, choisir un nombre de, un à dix, valeur inconnue « n ».Étape : ajouter 6, leur inconnue et 6 bâtons, « n » plus 6.Étape, soustraire 3, inconnue et 3 bâtons, « n » plus 3.Étape, ajouter 5, inconnue et 8 bâtons, « n » plus 8.Étape, ajouter 2, inconnue et dix bâtons, « n » plus dix.Étape, soustraire dix, inconnue, « n ».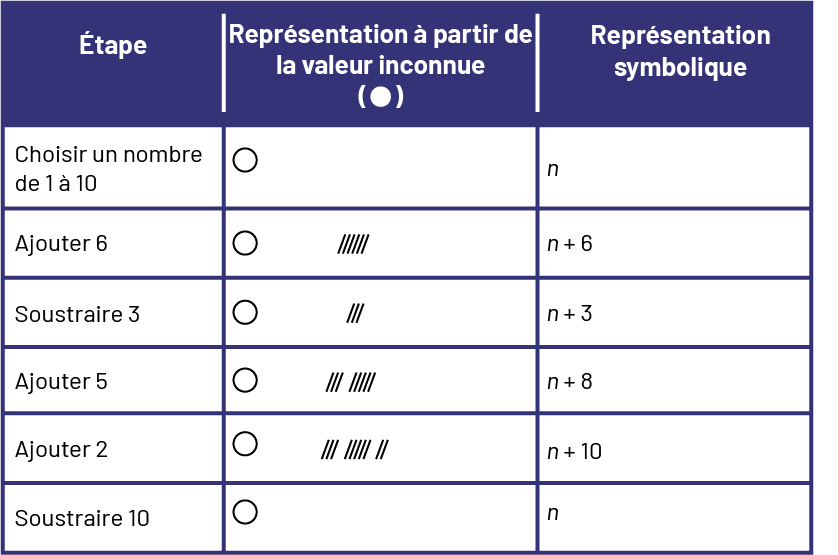
Former des équipes de deux élèves et remettre à chaque équipe une copie de l’annexe 6.5 (Représentation symbolique de la deuxième énigme). Demander aux élèves d’écrire une expression algébrique correspondant aux résultats de chaque étape de la deuxième énigme.
Exemple
image Tableau qui représente l’étape, la représentation à partir de la valeur inconnue et la représentation symbolique.Étape, choisir un nombre de, un à 5, inconnue, « n ».Étape, doubler le nombre, 2 inconnues, 2 multiplié par « ».Étape, ajouter 6, 2 inconnues et 6 bâtons, 2 multiplié par «n » plus 6.Étape, doubler la somme, 4 inconnues et 12 bâtons, 4 multiplié par « n » plus 12.Étape, soustraire 4, 4 inconnues et 8 bâtons, 4 multiplié par « n » plus 8.Étape, diviser par 4, une inconnue et 2 bâtons, 2 plus « n ».Étape : soustraire 2, une inconnue, « n ».
Animer une discussion au sujet des différentes expressions algébriques en reconnaissant la possibilité d’avoir plusieurs expressions algébriques équivalentes pour une même étape.
Source : Guide d’enseignement efficace des mathématiques de la 4e à la 6e année, p. 184-185.