La vue d'ensemble

At a Glance...

The Guides for Effective Instruction in Mathematics Revised

FrançaisEnglish

C3. Solve problems and create computational representations of mathematical situations using coding concepts and skills.

Learning Situation: Little Fish, Little Fish

Total Duration: approximately 120 minutes

Summary

Students code a video game that involves giving directions to a sprite to perform translations on a Cartesian plane in order to "catch another sprite".

Overall Expectations Specific Expectations
B1. Demonstrate an understanding of numbers and make connections to the way numbers are used in everyday life.

B1.1 Read and represent whole numbers up to and including one million, using appropriate tools and strategies, and describe various ways they are used in everyday life.
C3. Solve problems and create computational representations of mathematical situations using coding concepts and skills. C3.1 Solve problems and create computational representations of mathematical situations by writing and executing efficient code, including code that involves conditional statements and other control structures.

C3.2 Read and alter existing code, including code that involves conditional statements and other control structures, and describe how changes to the code affect the outcomes and the efficiency of the code.
E1. Describe and represent shape, location, and movement by applying geometric properties and spatial relationships in order to navigate the world around them. E1.3 Plot and read coordinates in all four quadrants of a Cartesian plane, and describe the translations that move a point from one coordinate to another.

Preferred High-Impact Instructional Practices in Mathematics Description
Problem-Solving Tasks and Experiences By using a context that is authentic to students, such as creating a video game, students demonstrate motivation and engagement in the activity. Problem solving often requires a lot of trial and error, while making connections with the student's personal experience. Students can then be invited to compare the tasks and determine what is similar and different between them.

Math Conversations

 By having math conversations about a concept that is both familiar (video games) and new (coding) to students, teachers are able to see what the student actually understands. Conversations deepen student thinking and challenge students to go beyond their basic knowledge and understanding. Connections and transfers to other strands are noticed during math conversations.

Prerequisite Knowledge and Skills
Basic knowledge of a block-based program in order to:
  • read and interpret commands;
  • move a sprite right, left, up, down;
  • create and alter the appearance of a sprite;
  • incorporate condition blocks;
  • change the size of the sprites;
  • change the canvas;
  • incorporate loops;
  • operate with coordinates of a point in the Cartesian plane (four quadrants);
  • use a number line;
  • become familiar with negative integers and their effect on an operation or a move.

At the end of this learning situation, the student will be able to:

  • write and organize code with the goal of making it into a video game, using knowledge of code conventions and efficiency;
  • read and represent integers using the number line;
  • plot and read coordinates in the four quadrants of the Cartesian plane.

Achievement Chart Criteraia

Skills Criteria 
Knowledge and Understanding

  • The student knows and understands blocks of code for a block-based program.
  • The student understands the effect of the negative sign on the location of a number on a number line.
  • The student uses coordinates on a Cartesian plane to determine the location of a sprite on the canvas.
Thinking

  • The student determines solutions to problems in the code (debugging).
  • The student analyzes or plans a coding project using pseudocode.
  • The student organizes their code while respecting conventions and taking efficiency into account (use a minimum of blocks in order to reach the desired outcome).
Communication

  • The student respects the syntax of the chosen coding program (puts the blocks in the right order and uses control structures that create efficient code).
Application

  • The student uses the properties of negative integers to program the movement of a sprite.
  • The student uses their knowledge of coding to create a game that includes the use of a Cartesian plane and integers.

Materials

computer with access to the chosen coding program

Note: The examples in this learning situation were created using Scratch.

Mathematical Vocabulary

coding, code, sequential events, concurrent events, repeating events, loop, condition (if, then, else), nested events, Cartesian plane, integer, coordinate, efficiency (in a coding context).

Before Learning (Warm-Up)

Duration: approximately 30 minutes

The assessment can be done by…

Unplugged Coding Activity 

Ask students to stand and imagine that they are at point (0, 0) of the Cartesian plane. If this is the first time students have worked with the four quadrants of the Cartesian plane, it would be beneficial to begin with a mini-lesson that shows students that the axes of the Cartesian plane are simply two number lines that intersect at 0, thus the point (0, 0). 

Encourage students to collaborate in teams, either by mixing diverse skill sets for peer teaching or by grouping them based on similar abilities for personalized instruction.

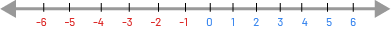
If the coordinates of the Cartesian plane have not yet been taught, this is a good time to introduce them, as students will benefit from this new learning immediately. As a support, if necessary, display the Cartesian plane with a numerical scale on the x and y axes as a reminder throughout the activity.

Ask students to determine, in the plane, where the point (2, 3) is in relation to their current position (0, 0). Ask them for directions to get to point (2, 3).

Sample answers:

  • You can take three steps up and two steps to the right.
  • You can take two steps to the right and three steps up.
  • You can point and drag diagonally from (0, 0) to (2, 3).

Repeat the exercise, but this time with the coordinates (-2, -3) relative to their initial position (0, 0).

Sample answers:

  • You can take three steps down and two steps to the left.
  • You can take three steps down and two steps to the left.
  • You can indicate the point and slide diagonally from (0, 0) to (-2, -3)

Point out to students that in everyday life, words such as to the right and up can be used, but it is also possible to describe movements using positive and negative numbers.

Present students with code blocks similar to these.

Note: For students who are very comfortable with coding, the blocks can be introduced at the same time. If this is a first exploration of coding or a coding program, the sequence below is suggested.

  • Advance () steps AND orient to ().
  • Add () to x AND add () to y AND go to x : () y : ()
  • Random number between () and ().

Ask students what they notice about the blocks. Answers may vary, but the important point to make is that the terminology used in the coding is additive (move forward, add, etc.). Ask students how a sprite can be moved across the entire Cartesian plane if it can only be "moved forward" or "added".

Possible answers

- Always start the sprite in the lower left corner in order to “move forward”.

This response is interesting because the student realizes that moving up and to the right requires addition. Students' prior knowledge of inverse operations can be used to help them recognize that moving left and down requires subtraction.

- Always use a "point towards" block to know the direction of travel.

This option is functional, but is much less efficient and risks creating errors in the code. That being said, a student who has difficulty with negative integers could use this strategy to better understand how the number line works. The operation of the “point towards” block, by its very nature, introduces students to the effect of the negative sign by using 90 degrees to point right and -90 degrees to point left.

Note: You have to click on 90 in order to enter a direction on the wheel.

Use positive movements for “up” and “right”, and negative movements for “down” and “left”.

This answer demonstrates an excellent understanding of the negative sign effect and is the most efficient way to program a move in a Cartesian plane. In coding, you have to use negative numbers to represent downward and leftward movements.

Active Learning (Exploration)

Duration: approximately 60 minutes

The assessment can be done by…

Guided Exploration – Positions on the Cartesian plane

For this activity ensure the coding program can:

  • allow a change of canvas;
  • operate with coordinates in the four quadrants of the Cartesian plane;
  • allow the student to perform translations by isolating the horizontal (x) and vertical (y) components.

When students are at their computer with a new blank project on the screen, ask them to choose a canvas that represents a Cartesian plane. It is possible that some Cartesian planes use different scales.

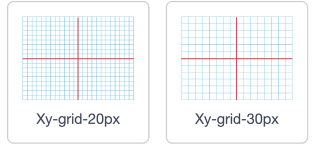
Here are two canvases that have two different scales, namely graduations every 20 pixels or every 30 pixels.
We can also see that the x axis and the y axis are highlighted with a different color.

Once the canvas is chosen, ask students questions related to scale to ensure understanding.

  • What is the typical unit of measurement for graphical elements on a canvas? (pixels)
  • How many "steps" (pixels) will it take for the sprite to move one square? (The answer depends on the scale. In the example above, the answer could be 20 steps (pixels) or 30 steps (pixels). This question can be answered by experimentation.)

Ask the students to choose a sprite and place it at the coordinates (0, 0) of the Cartesian plane. In order for it to be at coordinates (0, 0) at the start of the game, the "go to" block could be added at the start of the code (after the green flag).

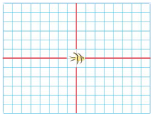
A sprite is placed at coordinates (0, 0) on a Cartesian plane in which the graduations
are, in this example, at 30 pixels from each other.

Provide the students with a list of coordinates to which their sprite should go using only the "add to x " and "add to y " blocks. The coordinates should be in all four quadrants of the plane; for example, starting from (0, 0), the sprite will need to go successively to the following coordinates:

(-3, 3)
(7, 4)
(-7, -4)
(2, -1)
(0, -3)

The students' task is to determine the translation needed for the sprite to travel to the new coordinates. The nature of the task causes the position of the sprite to change, so the starting point of the sprite is constantly changing. Here is an example of code that respects the first two translations in the list:

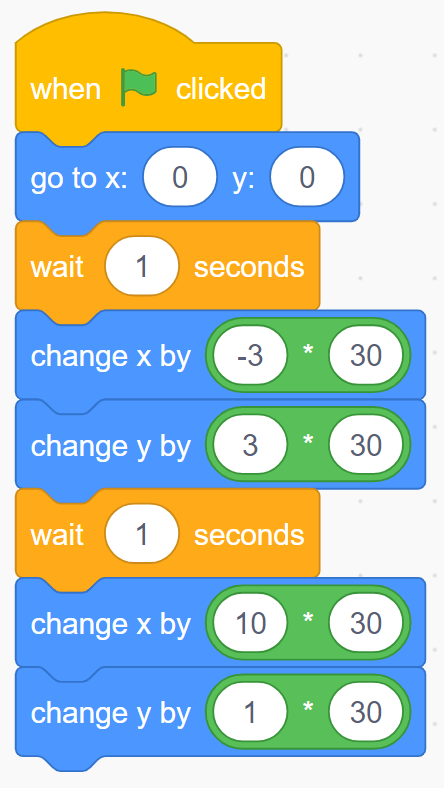
 We see two translations in this code. The coordinates of the first starting point are (0, 0). The first translation is the same as the coordinates of the final position, which is (-3, 3).

For the second translation, the new starting point (-3, 3) must be considered. So the translation in x is 10 and the translation in y is 1.

This last movement is compared to the integers located on a number line; for example, to go from –3 to +7, a movement of 10 units to the right is necessary (horizontal number line). The same principle applies for a movement in y, which is upwards (vertical number line). Encourage the students to use a number line in order to better define the desired movement.

Note that the operation blocks that multiply each number by 30 are essential in order to respect the scale of the Cartesian plane which, in this example, includes graduations of 30 pixels.

Help students code the movements of the sprite according to various coordinates of a Cartesian plane.

Following the guided exploration, ask students if it is efficient (and realistic) to code all possible sprite positions on the screen in the context of a game. The answer is no. Ask them what alterations might make the code more efficient or functional.

Possible answers

  • We could use the “go to (x) (y)” block, which does the translation for us without us having to calculate it.
  • One could use the "go to random position" block, which eliminates the predictability of the sprite's location.
  • The 30 pixel scale is useful for the Cartesian plane canvas, but with a different background one can use the current coordinates instead of always multiplying by 30, which would allow for more accurate positions.

This block would allow a sprite to move at random coordinates on a Cartesiane plane with a scale of 30 pixels.

In the sample game below, some answers can be found in the code.

Programming an Interactive Game

Challenge students to create a game to be shown to a peer. The objective of the game is to test the peer's knowledge of the description of translations in the four quadrants of the Cartesian plane. The game will consist of moving a sprite using translation vectors (coordinates) so that it touches various objects.

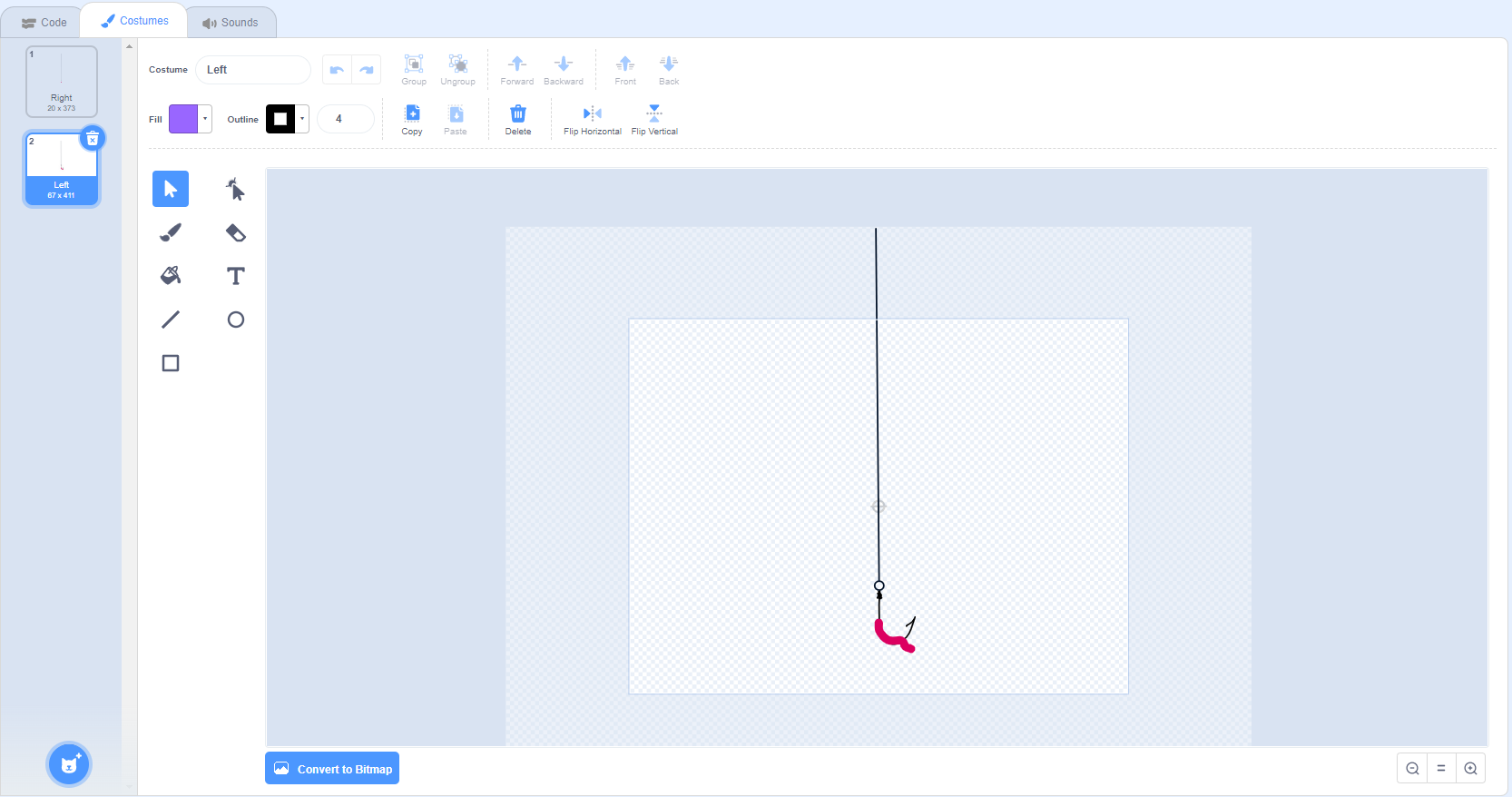
There are several possibilities of games that could test the understanding of these concepts. Here is an example of a fishing game that the student could produce:

Hook Sprite Code Fish Sprite Code

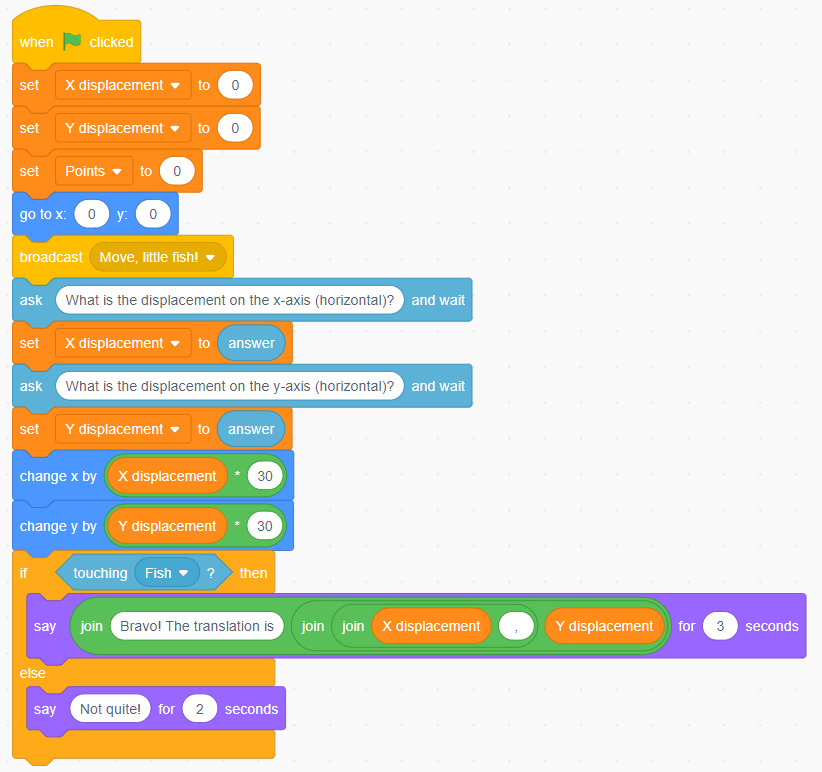
Note: In this code, we see the use of variables that will determine the movements necessary for the hook to "catch" the fish. We also see the use of a "message". Messages allow sprites to interact more and can be very useful in the context of coding a game. In this case, when the message "Move, little fish!" is sent, the fish sprite receives the message and executes the code.

We also see the use of the “group” block, which makes the code less cumbersome by avoiding using four different “say” blocks to communicate with the user.

This is what the game interface might look like:

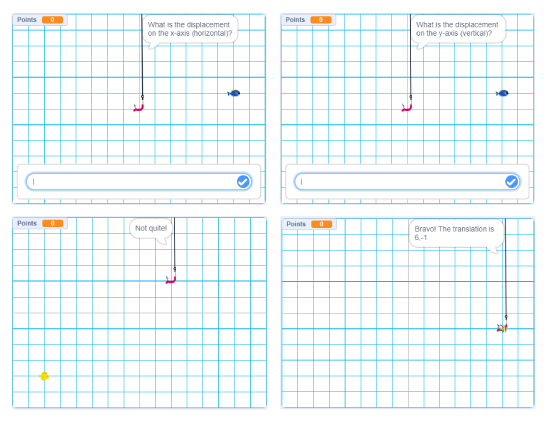
Note: The screenshots were taken from the full screen interface of the program at different times during the game.

Go Further – The Fishing Game

There are many ways to make the game more interactive and fun for the user. Encourage students to make the game as interactive as possible. Here are some suggestions:

  • Add a variable that can count the score and repeat the code until the user succeeds a certain number of times.
  • Use a different scale on the Cartesian plane to create an easier or more difficult level.
  • Add a time element, like a stopwatch that would count down.
  • Code the fish to stay in place for a specific number of seconds.

Here is an example of code that incorporates the scoring and repeating elements:

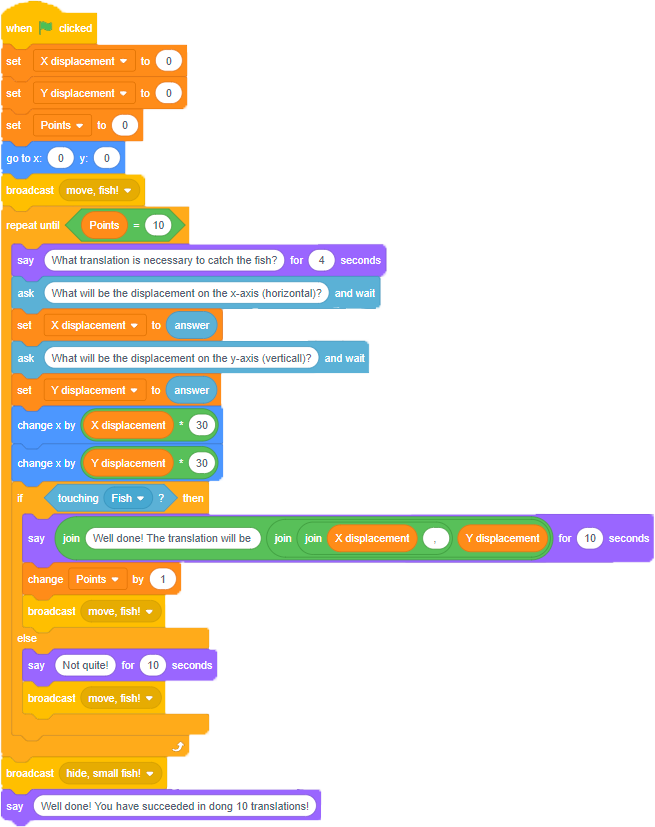
Possible Observations Possible Interventions
The student cannot move their sprite to the given coordinates. Remind the student that a pixel is very small and that a scale has to be used to obtain the desired translation.

Check that the student has coded the starting position as (0, 0), and that the sprite is placed back in that location to resume the code.
The student does not know how to alter or create a sprite. Deconstruct with the student the way the program works and review how to add a sprite.

Ask the student if they notice anything on the page that might help.

The hook used in the example is drawn by hand. Students can choose existing sprites or create or alter a sprite in the "costumes" menu.
The student is unable to use variables well. Question the student to check their understanding of the "variable" block.

  • How would you describe to me what a variable is?
  • Which values change in your code?

It can also be beneficial to make all the variables visible on the interface so that the student can take into account the value associated with each of them.
The student does not use the “group” block to create complex sentences with variables. The "group" block can be a bit intimidating at first. Pseudocode can help support the understanding of its purpose. In the code example above, the "group" block is used to communicate the translation to the student. The pseudocode might look like this:

Say, "Well done! The translation will be (variable move in x), (variable move in y)."

First you have to create a "join" block with four elements (ovals). Example:
The student has difficulty using conditional structures. Have the student verbalize the intent of their code or write pseudocode. Find the places where you see words indicating conditions (if, then, until, when).

Consolidation

Duration: approximately 30 minutes

A sprite is placed at coordinates (0, 0) on a Cartesian plane in which the tick marks are 30 pixels apart.

Have a fair with the students so they can try out the games. Have them note the similarities and differences between the games they tried and their own game. Encourage feedback from peers as they try the game.

Guide reflection through questioning.

  • What are the main differences between the codes? Is there more than one way to code the desired outcome? (Yes, there are many ways to write code. It's likely that the codes in the class will be similar, but not identical.)
  • Would it be possible to make the game easier (for example, adding numbers to the axes) or more difficult (for example, removing the grid and requiring position prediction)?
  • Have you noticed elements in other codes that you would like to integrate into yours (for example, more precise visual or textual elements, more efficient sequences, specialized blocks, such as Boolean blocks, or conditional loops)?

Extension

Have students program a trivia game in which a sprite must travel to specific coordinates. The student would first have to enter the necessary translations in order to move from one coordinate to another. Adding a block to trace the path could reveal a shape or mystery message indicating that the student has successfully moved their sprite to the correct places. During the game trial, encourage peer feedback.

The "pen in writing position" block is an example of a block that allows you to trace the path of the sprite.
This block is part of the Scratch coding program. In other programs, this type of block could have a different name.

Connections With Other Curriculum Expectations

Number

B2.1 Use the properties of operations, and the relationships between operations, to solve problems involving whole numbers, decimal numbers, fractions, ratios, rates, and whole number percents, including those requiring multiple steps or multiple operations.

A multi-step problem can quickly become a multi-line code. Efficiency can therefore come as a support in order to simplify a more complex problem, for example, by using loops, variables or custom blocks.

Spatial Sense

E1.4 Locate and read coordinates in the four quadrants of a Cartesian plane, and describe movements from one coordinate to another using translations.

The Cartesian plane is often used to show position and movements in visual coding contexts. It is therefore possible to ask the student to make several movements using the coordinates on the Cartesian plane. The student can later make their code more efficient by organizing the moves and using custom loops and blocks.

Financial Literacy

F1.4 Explain the concept of interest rates, and identify types of interest rates and fees associated with different accounts and loans offered by various banks and other financial institutions.

Interest scenarios, especially compound interest, can easily become multiple lines of code. Using variables, custom blocks, and generalizations can simplify code (and make a complex financial situation easier to understand).

Differentiated Instruction and Universal Design for Learning

  • Have the student create some pseudocode before they begin to create a blueprint for their programming.
  • Determine the variables with the student at the start of an activity.
  • Provide incomplete code for the student to alter.
  • Provide cheat sheets with the functions of the different blocks.
  • Invite students to work in teams, either heterogeneous to encourage peer teaching, or homogeneous to encourage direct and personalized instruction according to their needs.
  • Encourage students to create levels in their game so that the difficulty gradually increases (for example, fish are not stationary, there are objects to avoid).