C3 Mettre en application ses habiletés en codage pour résoudre des problèmes et créer des représentations de situations mathématiques de façon computationnelle à l’aide de concepts et d’habiletés en codage.
Situation d’apprentissage : petit poisson, petit poisson
Durée approximative : 120 minutes
Sommaire
Les élèves devront coder un jeu vidéo qui consiste à donner des directives à un sprite afin d’effectuer des translations sur un plan cartésien dans le but « d’attraper un autre sprite ».
| Attentes | Contenus d'apprentissage |
| Nombres B1. Démontrer sa compréhension des nombres et établir des liens avec leur utilisation dans la vie quotidienne. |
B1.1 Lire et représenter des nombres entiers à l’aide d’outils et de stratégies, y compris des droites numériques horizontales et verticales. |
| Algèbre C3. Résoudre des problèmes et créer des représentations de situations mathématiques de façon computationnelle en écrivant et en exécutant des codes efficaces, y compris des codes comprenant des instructions conditionnelles et d’autres structures de contrôle. |
C3.1 Démontrer sa compréhension des nombres et établir des liens avec leur utilisation dans
la vie quotidienne.
C3.2 Lire et modifier des codes donnés, y compris des codes comprenant des instructions conditionnelles et d’autres structures de contrôle, et décrire l’incidence de ces changements sur les résultats et l’efficacité. |
| Sens de l'espace E1. Décrire et représenter la forme, la position et le déplacement en se servant de propriétés géométriques et de relations spatiales pour s’orienter dans le monde qui l’entoure. |
E1.3 Situer et lire des coordonnées dans les quatre quadrants d’un plan cartésien, et décrire les déplacements d’une coordonnée à l’autre à l’aide de translations. |
| Pratiques pédagogiques à fort impact en mathématiques à privilégier | Description |
| Tâches et expériences de résolution de problèmes | En utilisant un contexte qui est authentique aux élèves, tel que la création d’un jeu vidéo, les élèves font preuve de motivation et d’engagement dans l’activité. Les résolutions de problèmes demandent souvent beaucoup d’essais et d’erreurs, tout en faisant des liens avec l’expérience personnelle de l’élève. On peut par la suite inviter les élèves à comparer les tâches et à déterminer ce qui est semblable et différent entre elles. |
|
Conversations mathématiques |
En ayant des conversations mathématiques au sujet d’un concept qui est à la fois bien connu (les jeux vidéo) et nouveau (le codage) pour les élèves, le personnel enseignant est en mesure de voir ce que l’élève comprend réellement. Les conversations permettent d’approfondir la réflexion de l’élève et lui demandent d’aller au-delà de sa connaissance et de sa compréhension de base. Des liens et des transferts vers d’autres domaines d’étude sont remarqués au cours des conversations mathématiques. |
|
Connaissances et habiletés préalables |
|---|
|
Résultats d’apprentissage
À la fin de cette situation d’apprentissage, l’élève pourra :
- créer et organiser un code en utilisant ses connaissances des conventions et de l’efficacité de celui-ci dans le but d’en faire un jeu vidéo;
- lire et représenter des nombres entiers en utilisant la droite numérique;
- situer et lire des coordonnées dans les quatre quadrants d’un plan cartésien afin de bien positionner les personnages de son jeu.
Critères d’évaluation selon les grilles d’évaluation du rendement
| Compétences | Critères d’évaluation |
| Connaissance et compréhension |
|
| Habiletés de la pensée |
|
| Communication |
|
| Mise en application |
|
Matériel requis
- ordinateur avec accès au logiciel choisi
- annexe Plan cartesien
Note : Les exemples dans cette situation d’apprentissage ont été conçus avec Scratch.
Vocabulaire mathématique
codage, code, événements séquentiels, événements simultanés, événements répétitifs, boucle, condition (si, alors, sinon), événements imbriqués, plan cartésien, nombre entier, coordonnée, efficacité (dans un contexte de codage)
Mise en situation
Durée approximative : 30 minutes
L’évaluation peut se faire par les…
Activité débranchée préparatrice au codage
Demander aux élèves de se tenir debout et d’imaginer qu’elles et ils sont au point (0, 0) d’un plan cartésien. Si c’est la première fois que les élèves travaillent avec les quatre quadrants d’un plan cartésien, il serait profitable de commencer par une minileçon qui montre aux élèves que les axes du plan cartésien sont simplement deux droites numériques qui se croisent à 0, donc le point (0, 0).
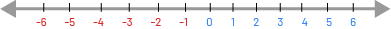
Si les coordonnées du plan cartésien n’ont pas encore été enseignées, c’est un bon moment de les présenter, car les élèves pourront profiter de ce nouvel apprentissage immédiatement. Comme appui, afficher, au besoin, un plan cartésien avec des nombres sur les axes des x et des y, qui servira d’aide-mémoire tout le long de l’activité.

Demander aux élèves de déterminer, dans le plan, l’endroit où se trouve le point (2, 3) par rapport à leur position actuelle (0, 0). Leur demander les directives qui permettraient de se rendre au point (2, 3).
Exemples de réponses :
- On peut faire deux pas à droite et trois pas vers le haut.
- On peut faire trois pas vers le haut et deux pas à droite.
- On peut indiquer le point et glisser en diagonale de (0, 0) à (2, 3).
Répéter l’exercice, mais, cette fois, avec le point (-2, -3) par rapport à leur position initiale (0, 0).
Exemples de réponses :
- On peut faire deux pas à gauche et trois pas vers le bas.
- On peut faire trois pas vers le bas et deux pas à gauche.
- On peut indiquer le point et glisser en diagonale de (0, 0) à (-2, -3)
Faire remarquer aux élèves que, dans la vie de tous les jours, on peut utiliser des mots tels à droite et vers le haut, mais qu’il est aussi possible de décrire des déplacements en utilisant des nombres positifs et négatifs.
Présenter aux élèves des blocs de code semblables à ceux-ci.
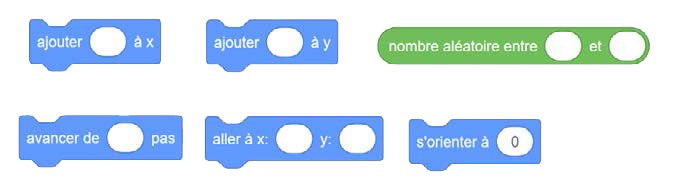 Image 6
blocs variables. 3 en haut et trois en bas. De gauche à droite en haut, ils sont les suivants: « ajouter » puis une
bulle vide « à » « x ». Suivis par, « ajouter » puis une bulle vide « à » « i grec ». Enfin, « nombre aléatoire
entre » puis une bulle vide « à » « i grec », « nombre aléatoire entre » puis une bulle vide « et » une autre bulle
vide. En bas, de gauche à droite d'abord : « avancer de » puis une bulle vide « pas ». Ensuite, « aller à « x » »
puis une bulle vide « pas », « aller à « x » » puis une bulle vide, « i grec » puis une bulle vide. Enfin, «
s'orienter à » puis une bulle marquée « zéro ».
Image 6
blocs variables. 3 en haut et trois en bas. De gauche à droite en haut, ils sont les suivants: « ajouter » puis une
bulle vide « à » « x ». Suivis par, « ajouter » puis une bulle vide « à » « i grec ». Enfin, « nombre aléatoire
entre » puis une bulle vide « à » « i grec », « nombre aléatoire entre » puis une bulle vide « et » une autre bulle
vide. En bas, de gauche à droite d'abord : « avancer de » puis une bulle vide « pas ». Ensuite, « aller à « x » »
puis une bulle vide « pas », « aller à « x » » puis une bulle vide, « i grec » puis une bulle vide. Enfin, «
s'orienter à » puis une bulle marquée « zéro ».
Note : Pour un groupe d’élèves qui est très à l’aise avec le codage et le logiciel en question, les blocs pourraient être présentés en même temps. Si c’est une première exploration du codage ou du logiciel, la séquence ci-dessous est suggérée.
- Avancer de ( ) pas ET s’orienter à ( ).
- Ajouter ( ) à x ET ajouter ( ) à y ET aller à x : ( ) y : ( )
- Nombre aléatoire entre ( ) et ( ).
Demander aux élèves ce qu’elles et ils remarquent au sujet des blocs. Les réponses peuvent varier, mais la remarque importante à soulever est que la terminologie utilisée dans le codage est additive (avancer, ajouter, etc.). Demander aux élèves la façon dont on peut déplacer un sprite sur tout le plan cartésien si l’on peut uniquement « avancer » ou « ajouter ».
Réponses possibles
- Il faut toujours commencer le sprite dans le coin inférieur gauche afin d’ « avancer ».
Cette réponse est intéressante, car l’élève réalise que les déplacements vers le haut et vers la droite nécessitent des additions. On peut utiliser les connaissances antérieures des élèves au sujet des opérations inverses afin de leur faire découvrir que les déplacements à gauche et vers le bas nécessitent des soustractions.
- Il faut toujours utiliser un bloc « s’orienter vers » afin de connaître la direction du déplacement.
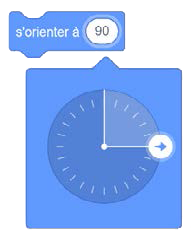
Cette option est fonctionnelle, mais est beaucoup moins efficace et risque de créer des erreurs dans le code. Cela étant dit, l’élève qui a de la difficulté avec les entiers négatifs pourrait utiliser cette stratégie afin de mieux comprendre le fonctionnement de la droite numérique. Le fonctionnement du bloc « s’orienter vers », par sa nature même, initie les élèves à l’effet du signe négatif en utilisant 90 degrés pour orienter vers la droite et -90 degrés pour orienter vers la gauche.
 Image
Une bulle variable sur la face d'une boussole. La bulle variable indique : « s'orienter à » puis une bulle marquée
« 90 ». Le compas indique la direction des 90 degrés dans le sens des aiguilles d'une montre.
Image
Une bulle variable sur la face d'une boussole. La bulle variable indique : « s'orienter à » puis une bulle marquée
« 90 ». Le compas indique la direction des 90 degrés dans le sens des aiguilles d'une montre. 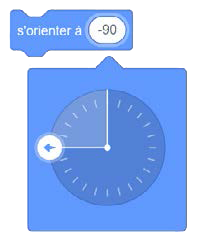 Image Une
bulle variable sur la face d'une boussole. La bulle variable indique : « s'orienter à » puis une bulle marquée «
-90 ». Le compas indique la direction des 90 degrés dans le sens contraire des aiguilles d'une montre.
Image Une
bulle variable sur la face d'une boussole. La bulle variable indique : « s'orienter à » puis une bulle marquée «
-90 ». Le compas indique la direction des 90 degrés dans le sens contraire des aiguilles d'une montre.
Note : Il faut cliquer sur 90 afin d’entrer une direction sur la roue.
- Il faut utiliser des déplacements positifs pour « en haut » et « à droite », et des déplacements négatifs pour « en bas » et « à gauche ».
Cette réponse témoigne d’une excellente compréhension de l’effet du signe négatif et correspond à la façon la plus efficace de programmer un déplacement dans un plan cartésien. Dans le monde du codage, il faut utiliser des nombres négatifs pour représenter les déplacements vers le bas et vers la gauche.
Déroulement
Durée approximative : 60 minutes
L’évaluation peut se faire par les…
Exploration guidée – Les positions sur le plan cartésien
Afin que la tâche puisse exploiter les apprentissages ciblés, le logiciel de codage choisi doit avoir certaines fonctionnalités. Le logiciel doit :
- permettre un changement d’arrière-plan;
- fonctionner avec des coordonnées dans les quatre quadrants du plan cartésien;
- permettre à l’élève d’effectuer des translations en isolant la composante horizontale (x) et verticale (y).
Lorsque les élèves sont devant leur ordinateur avec un nouveau projet vierge à l’écran, leur demander de choisir un arrière-plan qui représente un plan cartésien. Il est possible que certains plans cartésiens utilisent différentes échelles.
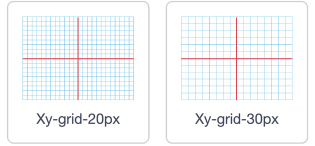 Image 2 arrière-plans qui ont 2 échelles différentes, soit des graduations tous les 20 pixels ou
tous les trente pixels. On voit aussi que l’axe des « x » et l’axe des « i grecs » sont mis en évidence avec une
couleur différente.
Image 2 arrière-plans qui ont 2 échelles différentes, soit des graduations tous les 20 pixels ou
tous les trente pixels. On voit aussi que l’axe des « x » et l’axe des « i grecs » sont mis en évidence avec une
couleur différente.
Voici deux arrière-plans qui ont deux échelles différentes, soit des graduations tous les 20 pixels ou tous les
30 pixels.
On voit aussi que l’axe des x et l’axe des y sont mis en évidence avec une couleur
différente.
Une fois l’arrière-plan choisi, poser aux élèves des questions liées à l’échelle afin d’assurer leur compréhension.
- Quelle est l’unité de mesure type des éléments graphiques sur un écran? (des pixels)
- Combien de « pas » (pixels) seront nécessaires afin que le sprite se déplace d’une case? (La réponse dépend de l’échelle. Dans l’exemple ci-dessus, la réponse pourrait être 20 pas (pixels) ou 30 pas (pixels). Cette réponse peut être découverte par expérimentation.)
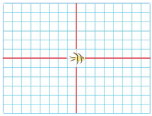
Demander aux élèves de choisir un sprite et de le placer aux coordonnées (0, 0) du plan cartésien. Afin qu’il soit aux coordonnées (0, 0) en début de jeu, le bloc « aller à » pourrait être ajouté au début du code (après le drapeau vert).
 Image
Un « sprite » en forme de poisson est placé aux coordonnées (parenthèse ouvrante) zéro, zéro 9parenthèse fermante)
sur un plan cartésien dans lequel les graduations se trouvent à 30 pixels les uns des autres. Le « sprite » est au
centre de la grille.
Image
Un « sprite » en forme de poisson est placé aux coordonnées (parenthèse ouvrante) zéro, zéro 9parenthèse fermante)
sur un plan cartésien dans lequel les graduations se trouvent à 30 pixels les uns des autres. Le « sprite » est au
centre de la grille.
Un sprite est placé aux coordonnées (0, 0) sur un plan cartésien dans lequel les graduations
se
trouvent à 30 pixels les unes des autres.
Fournir à l’élève une liste de coordonnées auxquelles leur sprite devra se rendre en utilisant uniquement les blocs « ajouter à x » et « ajouter à y ». Les coordonnées devraient se trouver dans les quatre quadrants du plan; par exemple, en partant de (0, 0), le sprite devra se rendre de façon successive aux coordonnées suivantes :
(7, 4)
(-7, -4)
(2, -1)
(0, -3)
La tâche de l’élève est de déterminer la translation nécessaire pour que le sprite se rende aux nouvelles coordonnées. La nature de la tâche fait en sorte que la position du sprite change, donc le point de départ du sprite change perpétuellement. Voici un exemple de code qui respecte les deux premières translations de la liste.
 Image Un bloc de code ou une séquence de code. Les séquences commencent par un bloc de
contrôle qui montre « quand » un drapeau vert « est cliqué ». Ensuite, « aller à « x » » puis une bulle vide
marquée « zéro » et « i grec » puis une autre bulle marquée « zéro ». Le bloc suivant est un bloc de
contrôle marqué « attendre » puis « un » et le mot « secondes ». Ci-dessous se trouvent les deux blocs
suivants pour chaque position « x » et « i grec ». Ils montrent « ajouter » et deux bulles indiquant la
portée avec une flèche descendante entre les deux. La portée est « moins trois » et « trente », puis « à » «
x ». Les axes « i grec » se lisent comme suit : « ajouter » et deux bulles indiquant l'étendue avec une
flèche descendante entre les deux. La portée est de « trois » et « trente » puis « à » « y ». Contrôle
suivant « attendre » puis « un » et le mot « secondes ». Enfin, les points « x » et « i grecs » suivants.
Ces blocs affichent « ajouter » et deux bulles indiquant la portée avec une flèche vers le bas entre les
deux. La portée est de « dix » et « trente », puis « à » « x ». Les axes « i grec » se lisent comme suit : «
ajouter » et deux bulles indiquant l'étendue avec une flèche descendante entre les deux. L'étendue est « un
» et « trente puis « à » « y ». Image Un bloc de code ou une séquence de code. Les séquences commencent par un bloc de
contrôle qui montre « quand » un drapeau vert « est cliqué ». Ensuite, « aller à « x » » puis une bulle vide
marquée « zéro » et « i grec » puis une autre bulle marquée « zéro ». Le bloc suivant est un bloc de
contrôle marqué « attendre » puis « un » et le mot « secondes ». Ci-dessous se trouvent les deux blocs
suivants pour chaque position « x » et « i grec ». Ils montrent « ajouter » et deux bulles indiquant la
portée avec une flèche descendante entre les deux. La portée est « moins trois » et « trente », puis « à » «
x ». Les axes « i grec » se lisent comme suit : « ajouter » et deux bulles indiquant l'étendue avec une
flèche descendante entre les deux. La portée est de « trois » et « trente » puis « à » « y ». Contrôle
suivant « attendre » puis « un » et le mot « secondes ». Enfin, les points « x » et « i grecs » suivants.
Ces blocs affichent « ajouter » et deux bulles indiquant la portée avec une flèche vers le bas entre les
deux. La portée est de « dix » et « trente », puis « à » « x ». Les axes « i grec » se lisent comme suit : «
ajouter » et deux bulles indiquant l'étendue avec une flèche descendante entre les deux. L'étendue est « un
» et « trente puis « à » « y ».
|
On voit, dans cette séquence de code, deux translations. Les coordonnées du premier point de départ sont (0,
0). La première translation ressemble aux coordonnées de la position finale, soit (-3, 3).
Pour la deuxième translation, il faut prendre en considération le nouveau point de départ (-3, 3). Donc, le déplacement en x sera de 10 et le déplacement en y sera de 1. Ce dernier déplacement se compare aux nombres entiers situés sur une droite numérique; par exemple, pour passer de –3 à +7, un déplacement de 10 unités vers la droite est nécessaire (droite numérique horizontale). Le même principe s’applique pour un déplacement en y, qui sera vers le haut (droite numérique verticale). Encourager l’élève à utiliser une droite numérique afin qu’elle ou il puisse mieux définir le déplacement voulu. À noter que les blocs d’opération qui multiplient chaque nombre par 30 sont essentiels afin de respecter l’échelle du plan cartésien qui, dans cet exemple, comprend des graduations de 30 pixels. |
Aider les élèves à coder les déplacements du sprite selon diverses coordonnées d’un plan cartésien.
À la suite de l’exploration guidée, demander aux élèves s’il est efficace (et réaliste) de coder toutes les positions possibles du sprite sur l’écran dans le contexte d’un jeu. La réponse est non. Leur demander les modifications qui pourraient rendre le code plus efficace ou plus fonctionnel.
Réponses possibles
- On pourrait utiliser le bloc « aller à (x) (y) », qui fera la translation pour nous sans qu’on ait à le calculer.
- On pourrait utiliser le bloc « aller à position aléatoire », ce qui élimine la prédictibilité de l’emplacement du sprite.
- L’échelle de 30 pixels est utile pour l’arrière-plan du plan cartésien, mais avec un arrière-plan différent, on peut utiliser les coordonnées actuelles au lieu de toujours multiplier par 30, ce qui permettrait des positions plus précises.
 Image Le
bloc de mouvement « aller à « x » » puis une bulle vide « nombre aléatoire entre » dans une couleur différente «
moins 6 » dans une bulle, « et » « 6 » dans une bulle « fois » « 30 » dans une dernière bulle, « i grec » axes : «
nombre aléatoire entre » de couleur différente « moins 4 » dans une bulle, « et » « 4 » dans une bulle « fois » « 30
» dans une dernière bulle.
Image Le
bloc de mouvement « aller à « x » » puis une bulle vide « nombre aléatoire entre » dans une couleur différente «
moins 6 » dans une bulle, « et » « 6 » dans une bulle « fois » « 30 » dans une dernière bulle, « i grec » axes : «
nombre aléatoire entre » de couleur différente « moins 4 » dans une bulle, « et » « 4 » dans une bulle « fois » « 30
» dans une dernière bulle.
Ce bloc permettrait à un sprite de faire des déplacements selon des coordonnées aléatoires sur un plan quadrillé ayant une échelle de 30 pixels.
Dans l’exemple de jeu ci-dessous, certaines réponses pourront être trouvées dans le code.
La programmation d’un jeu interactif
Donner aux élèves le défi de créer un jeu qui sera ensuite montré à un pair. Le but du jeu est de tester les connaissances du pair sur la description de translations dans les quatre quadrants du plan cartésien. Le jeu consistera à déplacer un sprite à l’aide de vecteurs de translation (coordonnées) afin qu’il touche des objets divers.
Il existe plusieurs possibilités de jeux qui pourraient vérifier la compréhension de ces concepts. Voici un exemple de jeu de pêche que pourrait produire l’élève :
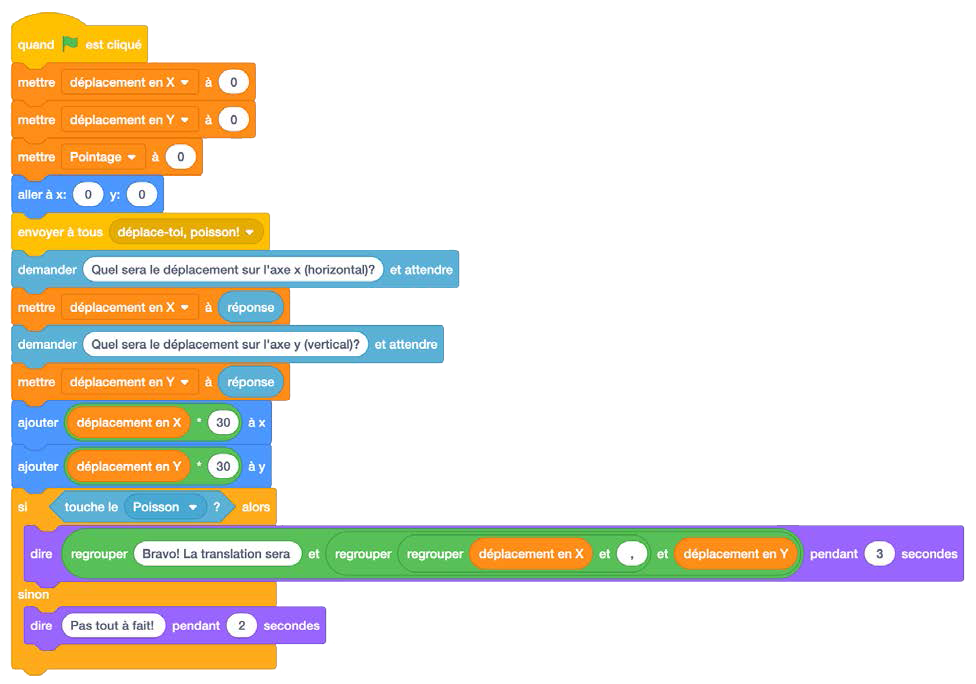
| Code du sprite « hameçon » | Code du sprite « poisson » |
 Un
bloc de codage commençant par un bloc de contrôle qui montre « quand » un drapeau vert « est cliqué ».
Empilé sur le bloc variable suivant qui montre le mot « mettre » puis « déplacement en « X » » avec une
flèche vers le bas, à côté de cela « à » « Zéro » dans une bulle. Sur le bloc de variables suivant qui
montre le mot « mettre » puis « déplacement en i grec » avec une flèche vers le bas, à côté de cela « à » «
Zéro » dans une bulle. Empilé sur le bloc de variables suivant qui montre le mot « mettre » « Pointage »
avec une flèche vers le bas, à côté de « à » « Zéro » dans une bulle. Suivis d'un bloc de mouvement marqué «
aller à « x » » : et une bulle indiquant « zéro », « i grec » : et une bulle indiquant « zéro ». Empilé sur
un bloc de contrôle « envoyer à tous » avec une bulle « déplace-toi, poisson! » avec une flèche descendante.
Ensuite est empilé un bloc de mouvement « demander » avec une bulle marquée « Quel sera le déplacement sur
l'axe horizontal « x » ? », « et les mots « et » « attendre ». Le bloc suivant est « mettre » puis «
déplacement en « X » », « avec une flèche vers le bas, à côté de « à » « réponse » dans une bulle. Ensuite
est empilé un bloc de mouvement « demander » avec une bulle marquée « Quel sera le déplacement sur l'axe « x
» (vertical) ?», « et les mots « et » « attendre ». Le bloc suivant est « mettre » puis « déplacement en « i
grec » « avec une flèche vers le bas, à côté de « à » « réponse » dans une bulle. En dessous, un bloc
variable indique « ajouter » et une bulle indique « déplacement en X » « fois » « 30 » dans une bulle puis «
à » « x ». Puis « ajouter » et une bulle indiquant « déplacement en « X » » « fois » « 30 » dans une bulle
puis « à » « i grec ». Enfin commence le bloc de condition commençant par le bloc « si » dans lequel se
trouve un bloc de mouvement « touche-le », « Poisson » avec une flèche vers le bas » avec un point
d'interrogation, et « alors ». Le tout est empilé sur le bloc son « dire » qui contient un opérateur et des
éléments variables. Ils sont regroupés comme suit : « regrouper », « Bravo ! La translation sera » dans une
bulle « et » « regrouper » « regrouper » variable « déplacement en « X » » dans une bulle, « et » et bulle
vide « et » variable « déplacement en i grec » dans une bulle, « pendant » « 3 » dans une bulle « secondes
». Il s'agit de la condition « sinon » bloc son incorporé « dire », « Pas tout à fait! » dans une bulle, «
pendant », « 2 » dans une bulle « secondes ». Un
bloc de codage commençant par un bloc de contrôle qui montre « quand » un drapeau vert « est cliqué ».
Empilé sur le bloc variable suivant qui montre le mot « mettre » puis « déplacement en « X » » avec une
flèche vers le bas, à côté de cela « à » « Zéro » dans une bulle. Sur le bloc de variables suivant qui
montre le mot « mettre » puis « déplacement en i grec » avec une flèche vers le bas, à côté de cela « à » «
Zéro » dans une bulle. Empilé sur le bloc de variables suivant qui montre le mot « mettre » « Pointage »
avec une flèche vers le bas, à côté de « à » « Zéro » dans une bulle. Suivis d'un bloc de mouvement marqué «
aller à « x » » : et une bulle indiquant « zéro », « i grec » : et une bulle indiquant « zéro ». Empilé sur
un bloc de contrôle « envoyer à tous » avec une bulle « déplace-toi, poisson! » avec une flèche descendante.
Ensuite est empilé un bloc de mouvement « demander » avec une bulle marquée « Quel sera le déplacement sur
l'axe horizontal « x » ? », « et les mots « et » « attendre ». Le bloc suivant est « mettre » puis «
déplacement en « X » », « avec une flèche vers le bas, à côté de « à » « réponse » dans une bulle. Ensuite
est empilé un bloc de mouvement « demander » avec une bulle marquée « Quel sera le déplacement sur l'axe « x
» (vertical) ?», « et les mots « et » « attendre ». Le bloc suivant est « mettre » puis « déplacement en « i
grec » « avec une flèche vers le bas, à côté de « à » « réponse » dans une bulle. En dessous, un bloc
variable indique « ajouter » et une bulle indique « déplacement en X » « fois » « 30 » dans une bulle puis «
à » « x ». Puis « ajouter » et une bulle indiquant « déplacement en « X » » « fois » « 30 » dans une bulle
puis « à » « i grec ». Enfin commence le bloc de condition commençant par le bloc « si » dans lequel se
trouve un bloc de mouvement « touche-le », « Poisson » avec une flèche vers le bas » avec un point
d'interrogation, et « alors ». Le tout est empilé sur le bloc son « dire » qui contient un opérateur et des
éléments variables. Ils sont regroupés comme suit : « regrouper », « Bravo ! La translation sera » dans une
bulle « et » « regrouper » « regrouper » variable « déplacement en « X » » dans une bulle, « et » et bulle
vide « et » variable « déplacement en i grec » dans une bulle, « pendant » « 3 » dans une bulle « secondes
». Il s'agit de la condition « sinon » bloc son incorporé « dire », « Pas tout à fait! » dans une bulle, «
pendant », « 2 » dans une bulle « secondes ».
|
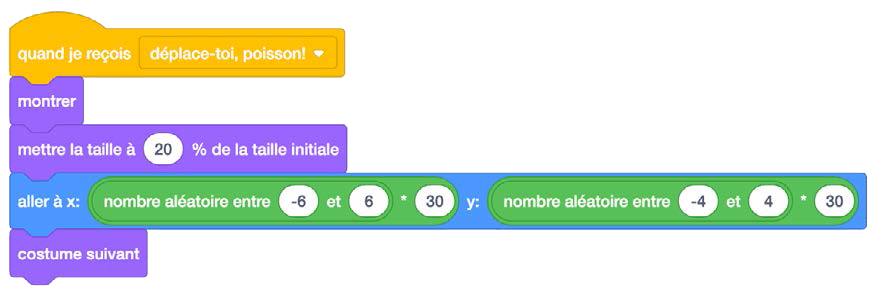 Image Un bloc de code commençant par un bloc d'événement « quand je reçois » et «
déplace-toi, poison » dans une autre case avec une flèche déroulante. Empilé sur un bloc d'apparence «
monter » sur un autre bloc d'apparence « mettre la taille a », « 20 », « pour cent de la taille initiale ».
Suivent un bloc de mouvement marqué « aller à « x » », « nombre aléatoire entre » dans une couleur
différente « moins 6 » dans une bulle, « et » « 6 » dans une bulle « fois » « 30 » dans une dernière bulle,
« i grec » axes : « nombre aléatoire entre » de couleur différente « moins 4 » dans une bulle, « et » « 4 »
dans une bulle « fois » « 30 » dans une dernière bulle. Se terminant par un bloc d'apparition « costume
suivant ». Image Un bloc de code commençant par un bloc d'événement « quand je reçois » et «
déplace-toi, poison » dans une autre case avec une flèche déroulante. Empilé sur un bloc d'apparence «
monter » sur un autre bloc d'apparence « mettre la taille a », « 20 », « pour cent de la taille initiale ».
Suivent un bloc de mouvement marqué « aller à « x » », « nombre aléatoire entre » dans une couleur
différente « moins 6 » dans une bulle, « et » « 6 » dans une bulle « fois » « 30 » dans une dernière bulle,
« i grec » axes : « nombre aléatoire entre » de couleur différente « moins 4 » dans une bulle, « et » « 4 »
dans une bulle « fois » « 30 » dans une dernière bulle. Se terminant par un bloc d'apparition « costume
suivant ».
|
Note : Dans ce code, on voit l’utilisation de variables qui détermineront les déplacements nécessaires afin que l’hameçon aille « attraper » le poisson. On voit aussi l’utilisation d’un « message ». Les messages permettent aux sprites d’interagir davantage et peuvent être très utiles dans le contexte du codage d’un jeu. Dans ce cas, lorsque le message « Déplace-toi, petit poisson! » est envoyé, le sprite du poisson reçoit le message et exécute le code.
On voit aussi l’utilisation du bloc « regrouper », qui rend le code moins encombrant en évitant d’utiliser quatre différents blocs « dire » pour communiquer avec l’utilisatrice ou l’utilisateur.
Voici ce à quoi l’interface du jeu pourrait ressembler :
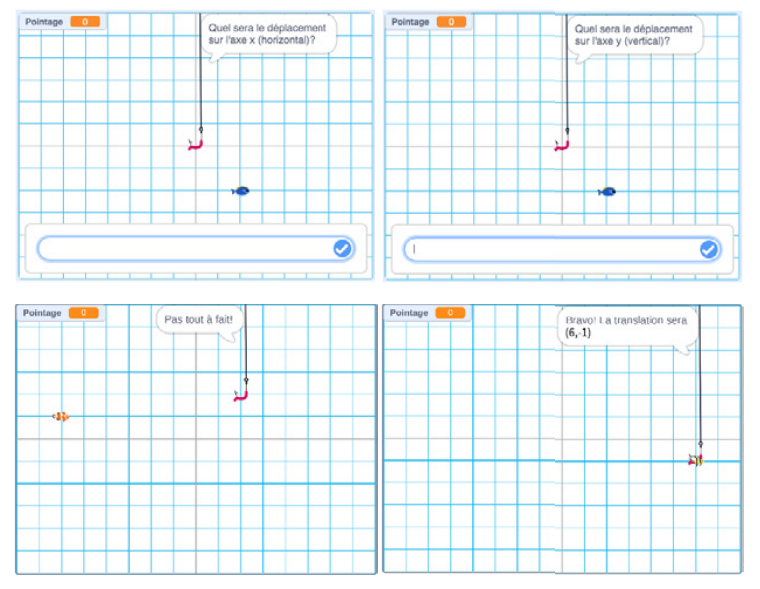 Image L'interface d'un jeu. Il y a 4 différents écrans en quadrillé de 2 par 2. Chaque écran
démontre un quadrillé
cartésien. Le premier écran en haut à gauche.Un ver au centre d'une grille graphique. Un poisson se trouve dans la
partie inférieure du côté droit, à deux lignes
de zéro. Une bulle de dialogue en haut de l'écran indique « Quel sera le déplacement sur l'axe « x » (horizontal)? ».
Le deuxième écran en haut à droite.Un ver au centre d'une grille graphique. Un poisson se trouve dans la partie
inférieure du côté droit, à deux lignes
de zéro. Une bulle de dialogue en haut de l'écran indique « Quel sera le déplacement sur l'axe « i grec » (vertical)?
».Le troisième écran en bas à gauche.Un ver se trouve maintenant à trois lignes de zéro dans le quadrant supérieur
droit. Le poisson est à la gauche. Une
bulle de dialogue indique : « Pas tout à fait! ».Le quatrième écran en bas à droite.Un ver se trouve à deux lignes du
quadrant droit, à une ligne en dessous de zéro. Le poisson est au même endroit que
le ver. Une bulle de dialogue indique « Bravo ! La traduction sera (parenthèse ouvrante) six, moins un (parenthèse
fermante) ».
Image L'interface d'un jeu. Il y a 4 différents écrans en quadrillé de 2 par 2. Chaque écran
démontre un quadrillé
cartésien. Le premier écran en haut à gauche.Un ver au centre d'une grille graphique. Un poisson se trouve dans la
partie inférieure du côté droit, à deux lignes
de zéro. Une bulle de dialogue en haut de l'écran indique « Quel sera le déplacement sur l'axe « x » (horizontal)? ».
Le deuxième écran en haut à droite.Un ver au centre d'une grille graphique. Un poisson se trouve dans la partie
inférieure du côté droit, à deux lignes
de zéro. Une bulle de dialogue en haut de l'écran indique « Quel sera le déplacement sur l'axe « i grec » (vertical)?
».Le troisième écran en bas à gauche.Un ver se trouve maintenant à trois lignes de zéro dans le quadrant supérieur
droit. Le poisson est à la gauche. Une
bulle de dialogue indique : « Pas tout à fait! ».Le quatrième écran en bas à droite.Un ver se trouve à deux lignes du
quadrant droit, à une ligne en dessous de zéro. Le poisson est au même endroit que
le ver. Une bulle de dialogue indique « Bravo ! La traduction sera (parenthèse ouvrante) six, moins un (parenthèse
fermante) ».
Note : Les captures d’écran ont été prises de l’interface du programme en plein écran à différents moments du jeu.
Aller plus loin – Le jeu de pêche
Il existe plusieurs façons de rendre le jeu plus interactif et plus amusant pour l’utilisatrice ou l’utilisateur. Encourager les élèves à rendre le jeu aussi interactif que possible. Voici quelques suggestions :
- Ajouter une variable qui pourra compter le pointage et faire répéter le code jusqu’à ce que l’utilisatrice ou l’utilisateur réussisse un certain nombre de fois.
- Utiliser un plan cartésien avec une différente échelle pour créer un niveau plus facile ou plus difficile.
- Ajouter un élément de temps, comme un chronomètre qui ferait un décompte.
- Coder les poissons pour qu’ils demeurent en place pendant un nombre de secondes précises.
Voici un exemple de code qui incorpore les éléments de pointage et de répétition :
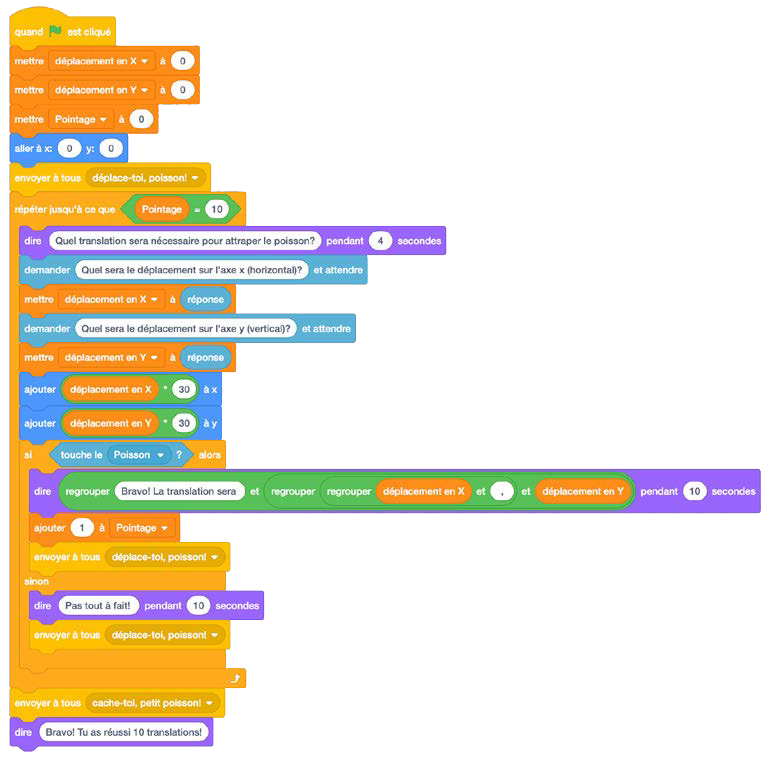 Image Blocs de codage attachés les uns aux autres. Bloc d’évènement : départ drapeau vert. 3 blocs
de variable : mettre « déplacement en « x » » à zéro. Mettre « déplacement en « y » » à zéro. Mettre « pointage » à
zéro. Bloc de mouvement : aller à « x » zéro, « y » zéro. Bloc d’évènement : envoyer à tous « déplace-toi, poisson!
Bloc de contrôle : répéter jusqu’à ce que « pointage égal dix ». Bloc d’apparence : dire quelle translation sera
nécessaire pour attraper le poisson? » pendant 4 secondes. Bloc de capteur : demander « quel sera le déplacement sur
l’axe de « x », horizontalement? » et attendre. Bloc de variable ; mettre « déplacement en « x » » à réponse. Bloc de
capteur : demander « quel sera le déplacement sur l’axe « y », vertical? » et attendre. Bloc de variable : mettre «
déplacement en « y » à réponse. 2 blocs de mouvement `ajouter « déplacement en « x » multiplié par, 30 à « x ».
Ajouter « déplacement en « y » » multiplié par, 30 à « y ». Bloc d’apparence : dire « regrouper, bravo! La translation
sera, et, regrouper, déplacement en « x », et point, et,
déplacement en « y », pendant dix secondes. Bloc de variable : ajouter un à « pointage ». Bloc d’évènement : envoyer à
tous « déplace-toi, poisson! Bloc de contrôle : sinon. Bloc d’apparence : dire « pas tout à fait », pendant dix
secondes. Bloc d’évènement : envoyer à tous « déplace-toi poisson! Répéter. Bloc d’évènement : envoyer à tous « cache
toi petit poisson! Bloc d’apparence « bravo! Tu as réussi dix translations.
Image Blocs de codage attachés les uns aux autres. Bloc d’évènement : départ drapeau vert. 3 blocs
de variable : mettre « déplacement en « x » » à zéro. Mettre « déplacement en « y » » à zéro. Mettre « pointage » à
zéro. Bloc de mouvement : aller à « x » zéro, « y » zéro. Bloc d’évènement : envoyer à tous « déplace-toi, poisson!
Bloc de contrôle : répéter jusqu’à ce que « pointage égal dix ». Bloc d’apparence : dire quelle translation sera
nécessaire pour attraper le poisson? » pendant 4 secondes. Bloc de capteur : demander « quel sera le déplacement sur
l’axe de « x », horizontalement? » et attendre. Bloc de variable ; mettre « déplacement en « x » » à réponse. Bloc de
capteur : demander « quel sera le déplacement sur l’axe « y », vertical? » et attendre. Bloc de variable : mettre «
déplacement en « y » à réponse. 2 blocs de mouvement `ajouter « déplacement en « x » multiplié par, 30 à « x ».
Ajouter « déplacement en « y » » multiplié par, 30 à « y ». Bloc d’apparence : dire « regrouper, bravo! La translation
sera, et, regrouper, déplacement en « x », et point, et,
déplacement en « y », pendant dix secondes. Bloc de variable : ajouter un à « pointage ». Bloc d’évènement : envoyer à
tous « déplace-toi, poisson! Bloc de contrôle : sinon. Bloc d’apparence : dire « pas tout à fait », pendant dix
secondes. Bloc d’évènement : envoyer à tous « déplace-toi poisson! Répéter. Bloc d’évènement : envoyer à tous « cache
toi petit poisson! Bloc d’apparence « bravo! Tu as réussi dix translations.
| Observations possibles | Pistes d’intervention |
| L’élève n’arrive pas à déplacer son sprite aux coordonnées indiquées. | Faire un rappel à l’élève qu’un pixel est très petit et qu’il faudra employer une échelle pour obtenir la
translation voulue.
Vérifier que l’élève a bien codé la position de départ comme étant (0, 0), et qu’elle ou il replace le sprite à cet endroit pour reprendre le code. |
| L’élève ne connaît pas la façon de modifier ou de créer un sprite. | Décortiquer avec elle ou lui le fonctionnement du logiciel et revoir la façon d’ajouter un sprite.
Demander à l’élève si elle ou il remarque quelque chose sur la page qui pourrait aider.
L’hameçon utilisé dans l’exemple est dessiné à la main. Les élèves peuvent choisir des sprites existants ou créer ou modifier un sprite dans le menu « costumes ». |
| L’élève n’arrive pas à bien utiliser les variables. | Questionner l’élève afin de vérifier sa compréhension du bloc « variable ».
Il peut aussi être profitable de rendre toutes les variables visibles sur l’interface afin que l’élève puisse tenir compte de la valeur associée à chacune d’elles. |
| L’élève n’utilise pas le bloc « regrouper » pour créer des phrases complexes ayant des variables. | Le bloc « regrouper » peut être un peu intimidant au début. Un pseudocode peut venir appuyer la
compréhension de son utilité. Dans l’exemple du code ci-dessus, le bloc « regrouper » est utilisé afin de
communiquer la translation à l’élève. Le pseudocode pourrait donc ressembler à ceci :
Dire : « Bravo! La translation sera (variable déplacement en x), (variable déplacement en y). » Il faut d’abord créer un bloc « joindre » ayant quatre éléments (ovales). Exemple :  Image Un bloc de code « regrouper », « Bravo ! La translation sera » dans une bulle « et » «
regrouper », « regrouper » variable « déplacement en « X » » dans une bulle, « et » et bulle vide « et »
variable « déplacement en i grec » dans une bulle. Image Un bloc de code « regrouper », « Bravo ! La translation sera » dans une bulle « et » «
regrouper », « regrouper » variable « déplacement en « X » » dans une bulle, « et » et bulle vide « et »
variable « déplacement en i grec » dans une bulle.
|
| L’élève a de la difficulté à utiliser les structures conditionnelles. | Demander à l’élève de verbaliser l’intention de son code ou d’écrire un pseudocode. Trouver les endroits où l’on voit des mots indiquant des conditions (si, lorsque, jusqu’à, quand). |
Observation
Durée approximative : 30 minutes
L'évaluation peut se faire par les...

Faire une foire avec les élèves pour qu’elles et ils puissent essayer les jeux. Leur demander de noter les ressemblances et les différences entre les jeux qu’elles et ils ont essayés et le leur. Encourager la rétroaction des pairs au cours de l’essai du jeu.
Guider la réflexion par le questionnement.
- Quelles sont les principales différences entre les codes? Y a-t-il plus d’une façon de coder le comportement voulu? (Oui, il existe plusieurs façons d’écrire un code. Il est probable que les codes dans la classe seront similaires, mais pas identiques.)
- Est-ce qu’il serait possible de rendre le jeu plus facile (par exemple, ajouter des nombres aux axes) ou plus difficile (par exemple, enlever le quadrillé et exiger la prédiction de la position)?
- As-tu remarqué des éléments, dans les autres codes, que tu aimerais intégrer au tien (par exemple, des éléments visuels ou textuels plus précis, des séquences plus efficaces, des blocs spécialisés, telles des booléennes ou des boucles conditionnelles)?
Consolidation
Proposer aux élèves de programmer un jeu-questionnaire dans lequel un sprite doit se rendre à des coordonnées précises. L’élève aurait d’abord à entrer les translations nécessaires afin de passer d’une coordonnée à l’autre. L’ajout d’un bloc permettant de tracer le trajet pourrait dévoiler une forme ou un message mystère indiquant que l’élève a réussi à déplacer son sprite aux bons endroits. Au cours de l’essai du jeu-questionnaire, encourager la rétroaction des pairs.

Le bloc « stylo en position d’écriture » est un exemple de bloc qui permet de tracer le parcours du
sprite.
Ce bloc fait partie du logiciel de codage Scratch. Dans d’autres logiciels, ce type de bloc
pourrait porter un nom différent.
Liens avec les autres domaines mathématiques
Nombres
B2.1 Utiliser les propriétés des opérations et les relations entre les opérations pour résoudre des problèmes comportant des nombres naturels, des nombres décimaux, des fractions, des rapports, des taux et des pourcentages, y compris des problèmes à plusieurs étapes ou plusieurs opérations.
Un problème à plusieurs étapes peut rapidement devenir un code à plusieurs lignes. L’efficacité peut donc venir en appui afin de simplifier un problème plus complexe, par exemple, en utilisant des boucles, des variables ou des blocs personnalisés.
Sens de l’espace
E1.4 Situer et lire des coordonnées dans les quatre quadrants d’un plan cartésien, et décrire les déplacements d’une coordonnée à l’autre à l’aide de translations.
Le plan cartésien est souvent utilisé pour montrer la position et les déplacements dans des contextes de codage visuel. Il est donc possible de demander à l’élève de faire plusieurs déplacements en utilisant les coordonnées du plan cartésien. L’élève peut par la suite rendre son code plus efficace en organisant les déplacements et en utilisant des boucles et des blocs personnalisés.
Littératie financière
F1.4 Expliquer le concept des taux d’intérêt et déterminer les types de taux d’intérêt et de frais associés à différents comptes et prêts offerts par diverses banques et autres institutions financières.
Les scénarios sur l’intérêt, surtout l’intérêt composé, peuvent facilement devenir plusieurs lignes de code. L’utilisation de variables, de blocs personnalisés et de généralisations permet de simplifier le code (et de rendre une situation financière complexe plus facile à comprendre).
Différenciation pédagogique et conception universelle de l’apprentissage
- Demander à l’élève de créer un pseudocode avant même de commencer afin de créer un plan pour sa programmation.
- Déterminer dès le début les variables avec l’élève.
- Fournir un code incomplet pour que l’élève le modifie.
- Fournir des aide-mémoire avec les fonctions des différents blocs.
- Inviter les élèves à travailler en équipes, soit hétérogènes pour encourager l’enseignement par les pairs, soit homogènes pour favoriser l’enseignement explicite et personnalisé selon leurs besoins.
- Encourager les élèves à créer des niveaux à leur jeu pour que la difficulté augmente graduellement (par exemple, les poissons ne sont pas stationnaires, il y a des objets à éviter).
Source : Guide d’enseignement efficace des mathématiques, Codage, p. 116-128.