C1.1 Identify and describe repeating, growing, and shrinking patterns, including patterns found in real-life contexts, and specify which growing patterns are linear.
Activity 1: How Can You Justify Your Answer?
Prepare the same cards for all students. One set of cards consists of pictorial representations of patterns and the other set of cards consists of number sequences. Have students answer the following questions:
Questions
- Which card shows a pattern with a recursive relation or a functional relation? Justify your answer.
- Which card shows a repeating pattern? Justify your choice.
- Which card shows a growing pattern? Justify your choice.
- Which card shows a shrinking pattern? Justify your choice.
- Which card shows a linear pattern? Justify your choice.
Pattern 1: Pictorial Representations
a)

b)

c)
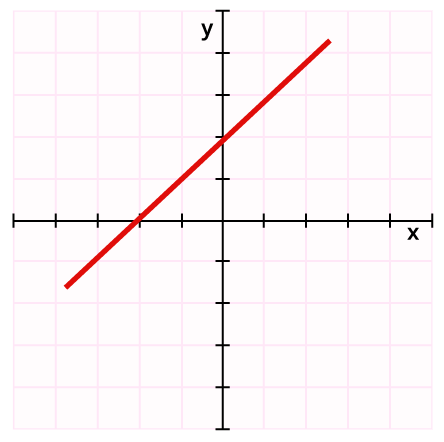
d)
Pattern 2: Number Sequences
- 30, (30 - 5), (30 - 2 x 5), (30 - 3 x 5)…
- 1, 4, 9, 16…
- 3, 6, 9, 12…
- 1000, 100, 10, 1…
Activity 2: Combinations (Linear Growing Pattern)
Give one paper strip to each student with a number pattern on it. Allow students a few minutes to individually analyze their pattern. Next, assign pairs using a random name or number generator. In pairs, have students take turns to explain if their patterns is:
- growing or shrinking;
- linear or non-linear.
Encourage the students to ask questions to their partners.
Repeat as desired.
