C2.1 Add monomials with a degree of 1 that involve whole numbers, using tools.
Activity 1: Area and Addition of Monomials
Materials
- colour tiles or virtual tiles

Have students represent a polygon with colour tiles using only one colour of tile. Ask them to choose a monomial of degree 1 to represent the area of one tile.
Afterwards, have students express the area of their polygon as an algebraic expression in two different ways (adding the monomials).
Have half of the students circulate around the classroom and observe the other students' polygons. Ask them to check whether the two algebraic expressions represent the area of the polygon constructed. Then alternate by having the other half of the students circulate around the classroom and observe the other students' work.
Example
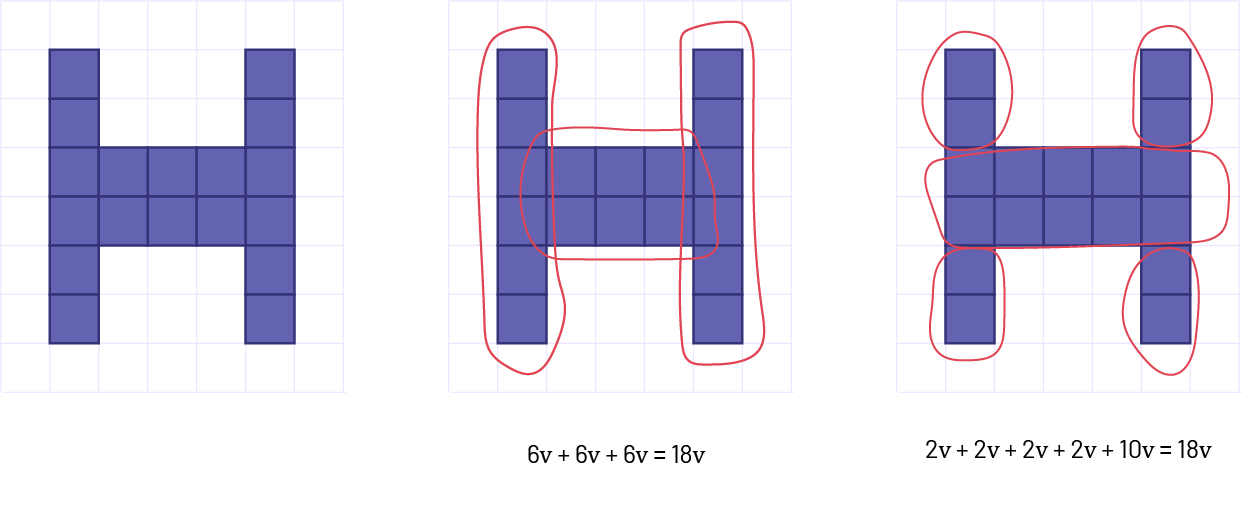
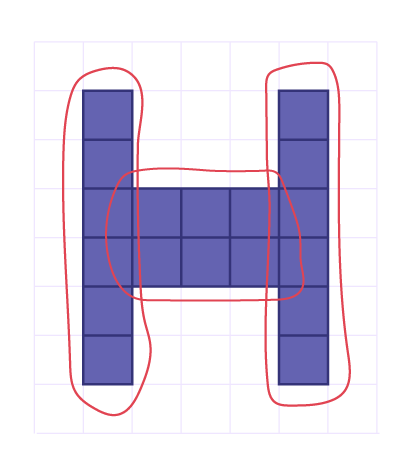
6v + 6v + 6v = 18v
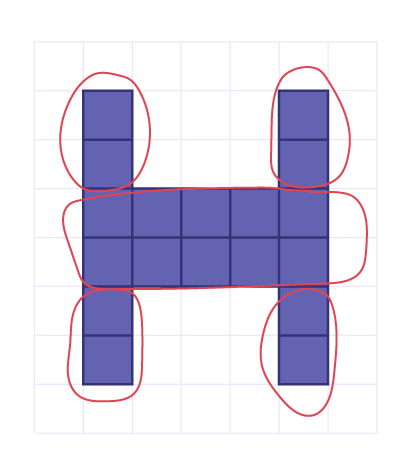
2v + 2v + 2v + 2v + 10v = 18v
Activity 2: Addition of Monomials With a Degree of 1
Present students with the following scenario:
Maëlie has 5 packages of apples, while Loïc has 3 packages. Write an algebraic expression to represent the total number of apples. Simplify the expression.
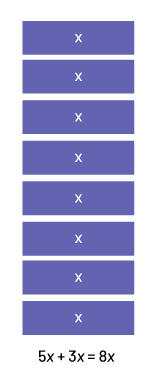
Strategy 1: Simplifying Algebraic Expression Using Repeated Addition
I wrote 5x +3x, as an algebraic expression, where x is the quantity of apples in each packages.
To simplify the expression, I can do repeated addition.
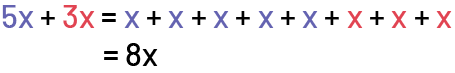
Strategy 2: Simplifying Algebraic Expression by Collecting Like Terms Algebraically
5x + 3x
Since 5x and 3x are like terms you add their coefficients.
(5 + 3)x = 8x
Strategy 3: Simplifying Algebraic Expression Using a Visual Representation
The first column represents 5x and the second column represents 3x. All together the tiles can be combined to give 8x.
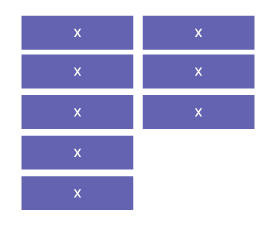
So:
Activity 3: Addition of Monomials
Ask students to add the following monomials:
- x + y + 2x + 3
Strategy 1
Representing Addition Using Words to Identify and Collect Like Terms
x + y + 2x + 3
1 group of x plus 2 groups of x is equal to 3 groups of x.
There are no terms to combine with the 1 group of y and similarly there are no terms to combine with the number 3.
So, the result is 3 groups of x plus 1 group of y plus 3.
3x + y + 3
Strategy 2
Representing Addition by Collection Like Terms Algebraically
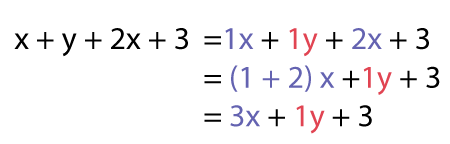
Strategy 3
Representing Addition by Collecting Like Terms Using a Visual Representation
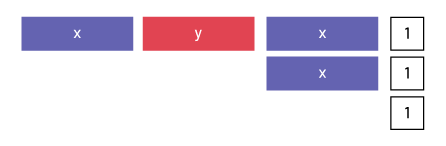
I can group like terms together.
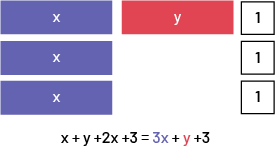
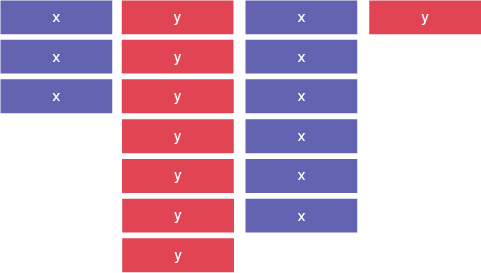
- 3x +7y +6x + y
Strategy 1
Representing Addition by Collecting Like Terms Algebraically
I can only add like terms.
I group like terms together.

For each set of like terms, I add numbers in front of the variable.

Strategy 2
Representing Addition by Collecting Like Terms Using Visual Representation
I can group like terms together.
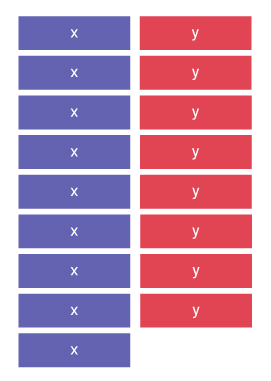
Source: translated from En avant, les maths!, 6e année, CM, Algèbre, Addition de monômes du premier degré, p. 2-6.
