C2.1 Additionner des monômes du premier degré comprenant des nombres naturels à l’aide d’outils.
Activité 1 : aire et addition de monômes
Matériel
- tuiles de couleur ou matériel virtuel

Demander aux élèves de représenter un polygone à l’aide de tuiles de couleur en n’utilisant qu’une couleur de tuiles. Vous pourriez leur demander de représenter une lettre de l’alphabet.
Par la suite, demander aux élèves de déterminer l’aire de leur polygone (additionner les monômes) de deux différentes façons en l’exprimant sous la forme d’une expression algébrique.
Demander à la moitié des élèves de circuler dans la salle de classe et d’observer les polygones des autres élèves. Leur demander de vérifier si les deux expressions algébriques représentent bien le polygone construit. Par la suite, alterner en demandant à l’autre moitié des élèves de circuler à leur tour dans la salle de classe pour observer les polygones des autres élèves.
Exemple
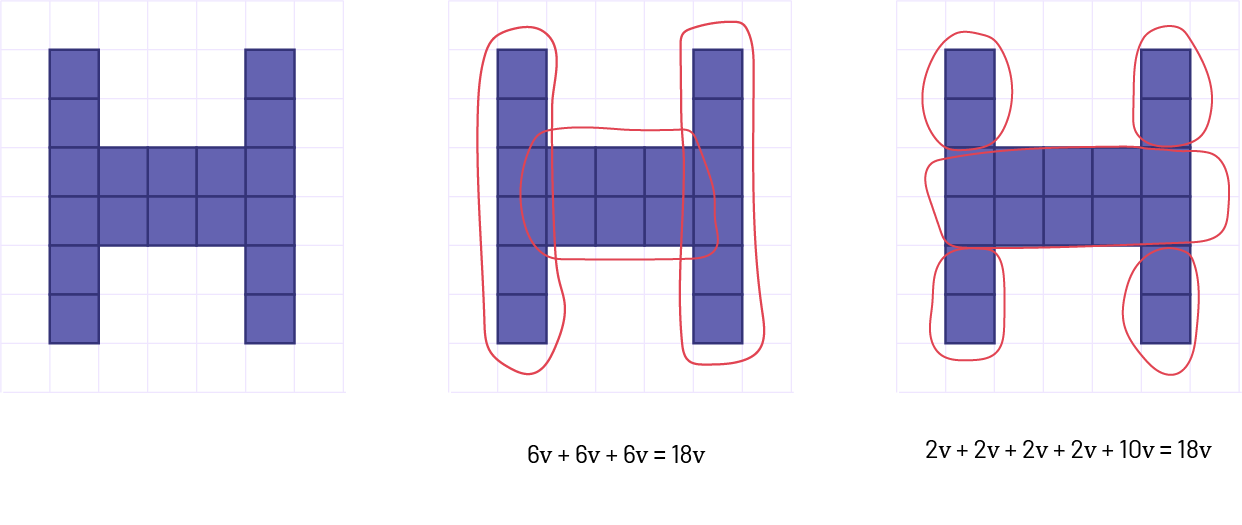 Image Figure un : polygone en forme de la lettre « h » majuscule. Elle est créée avec 18 carrés.
Figure 2 : polygone en forme de la lettre « h » majuscule. Elle est créée avec 18 carrés. Les groupes de 6 carrés
sont encerclés. Figure 3 : polygone en forme de la lettre « h » majuscule. Elle est créée avec 18 carrés. 4 groupes de
2 et un groupe
de dix sont encerclés.
Image Figure un : polygone en forme de la lettre « h » majuscule. Elle est créée avec 18 carrés.
Figure 2 : polygone en forme de la lettre « h » majuscule. Elle est créée avec 18 carrés. Les groupes de 6 carrés
sont encerclés. Figure 3 : polygone en forme de la lettre « h » majuscule. Elle est créée avec 18 carrés. 4 groupes de
2 et un groupe
de dix sont encerclés.
Activité 2 : addition de monômes du premier degré
Présenter aux élèves la situation suivante :
Maëlie a 5 paquets de pommes, tandis que Loïc en a 3 . Combien de pommes ont-ils en tout? Écris une expression algébrique qui représente cette situation et résous le problème.
Stratégie 1 : Calculs effectués à l’aide de l’addition répétée
J’ai écrit 5x + 3x, comme expression algébrique, où x est la quantité de pommes.
Pour résoudre l’expression, je peux faire une addition répétée.
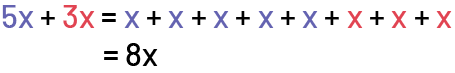
Stratégie 2 : Calculs effectués à l’aide d’une expression algébrique (ou d’une représentation symbolique)
5x + 3x
Je regroupe les termes semblables pour simplifier l’expression.
(5 + 3)x = 8x
Stratégie 3 : Calculs effectués à l’aide d’une représentation concrète ou visuelle
Je peux regrouper tous les termes semblables.
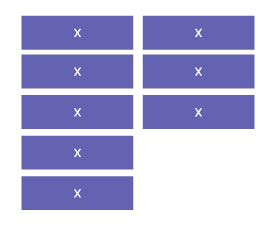
Alors :
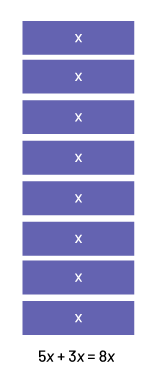
Activité 3 : addition de monômes
Demander aux élèves d’additionner les monômes suivants :
- x + y + 2x + 3
Stratégie 1
Calculs effectués à l’aide de mots
x + y + 2x + 3
1 groupe de x + 2 groupes de x = 3 groupes de x
1 groupe de y
Le nombre 3
Donc, j’obtiens 3 groupes de x + 1 groupe de y + 3
3x + y + 3
Stratégie 2
Calculs effectués à l’aide d’une expression algébrique
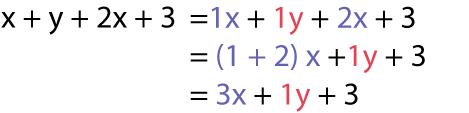 «
x » plus « y » plus 2 « x » plus 3 égal un « x » plus un « Y » plus 2 « x » plus 3. Égal (parenthèse ouvrante) un plus
2 (parenthèse fermante) « x » plus un « y » plus 3. Égal 3 « x » plus un « y » plus 3.
«
x » plus « y » plus 2 « x » plus 3 égal un « x » plus un « Y » plus 2 « x » plus 3. Égal (parenthèse ouvrante) un plus
2 (parenthèse fermante) « x » plus un « y » plus 3. Égal 3 « x » plus un « y » plus 3.
Stratégie 3
Calculs effectués à l’aide d’une représentation concrète ou visuelle
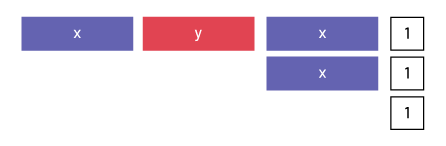 Image
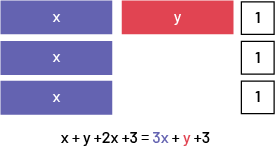
Première ligne : bloc « x », bloc « y », bloc « x » un carré noté un.Deuxième ligne : un bloc « x », un carré noté un.
Troisième ligne : un carré noté un.
Image
Première ligne : bloc « x », bloc « y », bloc « x » un carré noté un.Deuxième ligne : un bloc « x », un carré noté un.
Troisième ligne : un carré noté un.
Je peux regrouper les termes semblables.
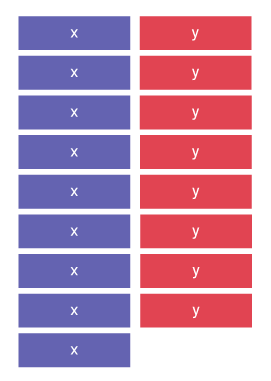
- 3x + 7y + 6x + y
Stratégie 1
Calculs effectués à l’aide d’une expression algébrique
Je peux uniquement additionner les termes semblables.
Je regroupe les termes semblables.

J’additionne les nombres devant les termes algébriques semblables.

Stratégie 2
Calculs effectués à l’aide d’une représentation concrète ou visuelle
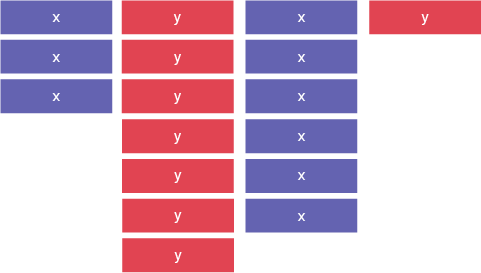
Je peux regrouper les termes semblables.
Source : En avant, les maths!, 6e année, CM, Algèbre, p. 3-6.
