C2.3 Solve equations that involve multiple terms and whole numbers in various contexts, and verify solutions.
Activity 1: Let's Keep Our Balance!
Draw a diagram on the board of the following situation:
Group students into teams of two. Ask them to write an equation representing the relation of equality; for example, 4 + a + a + a + a = 9 + a + a + 7 or 4 + 4a = 9 + 2a + 7.
Tell students that they must determine the value of the variable (the cube, the letter a) using the model of the mathematical balance or an equation. Remind them, if necessary, that in the same situation, each variable represented by the same symbol must have the same value. Allow students the time needed to complete the task. Then, lead a mathematical discussion on the different strategies used to determine the value of the variable (a = 6). Point out strategies used such as:
- Change the equation; for example, by removing a twice on each side, the equality is maintained, and we then analyze the equation 4 + a + a = 9 + 7. Then by removing 4 on each side, the equality is maintained, and the equation a + a = 9 + 3 is analyzed.
- Conduct systematic testing.
Suggest other similar situations of equality.
Example
Ask students to write an equation that represents a situation of equality, then replace one variable with a value and determine the value of the other:
Example
6 + c = 5 + s + 4
If c = 3, then s = 0
If c = 10, then s = 7
Note: The different values can be written in a table of values.
| c | 3 | 10 | |||
|---|---|---|---|---|---|
| s | 0 | 7 |
Source: translated from Guide d’enseignement efficace des mathématiques de la 4e à la 6e année, Modélisation et algèbre, p. 186-187.
Activity 2: The Strawberry Field
A fruit grower has 768 strawberry plants to sow this year. There are 24 rows ready in the garden for 30 to 35 plants each. Using an array, determine the number of strawberry plants per row that the grower will need to sow in which all the rows have the same amount of strawberries plants.
The Strawberry Field (Answer Sheet)
Therefore, he needs to plant 32 plants per row.
Source: translated from L’@telier - Ressources pédagogiques en ligne (atelier.on.ca).
Activity 3: Rolling Equalities!
Write the equal (=) sign on the board and explain the following activity:
We will create equations using dice and pattern blocks. Two students will take turns rolling two dice and randomly choosing a pattern block. The numbers on Student A's dice and his pattern block will be used to create the algebraic expression that will appear to the left of the equal sign in the equation and Student B's will make up the algebraic expression to the right of the sign.
For example, if Student A rolls 3 and 4 on the dice and draws a green triangle, they will write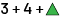 
to the left of the = sign.
If Student B rolls 4 and 6 on the dice and draws a beige rhombus, they will write 
to the right of the = sign.
Next, assign values to the pattern blocks while making sure to maintain the equality relationship; for example, if Student A assigns a value of 4 to the green triangle, Student B must assign a value of 1 to the beige rhombus.
Remind students that in an equation, two different symbols, such as a green triangle and a beige rhombus, may have the same value, but two identical symbols, such as two beige rhombuses, always have the same value.
It is possible that in some situations equality cannot be established; for example, in the equation 
, equality cannot be established. Therefore, this equation is rejected.
Source: translated from Guide d’enseignement efficace des mathématiques de la 4e à la 6e année, Modélisation et algèbre, p. 132.