C2.3 Résoudre des équations qui comprennent des termes multiples et des nombres naturels dans divers contextes, et vérifier les solutions.
Activité 1 : Gardons l’équilibre!
Dessiner, au tableau, le schéma de la situation suivante.

Grouper les élèves en équipes de deux. Leur demander d’écrire une équation représentant la relation d’égalité; par exemple, 4 + a + a + a + a = 9 + a + a + 7 ou 4 + 4a = 9 + 2a + 7.
Annoncer aux élèves qu’elles et ils doivent déterminer la valeur de la variable (le cube, la lettre a) à l’aide du modèle de la balance mathématique ou de l’équation. Leur rappeler, au besoin, que, dans une même situation, chaque variable représentée par un même symbole doit avoir la même valeur. Allouer aux élèves le temps nécessaire pour accomplir la tâche demandée. Puis, animer un échange mathématique sur les différentes stratégies employées pour déterminer la valeur de la variable (a = 6). Faire ressortir les stratégies utilisées telles que :
- Modifier l’équation; par exemple, en enlevant a deux fois de chaque côté, l’égalité est maintenue, et l’on analyse alors l’équation 4 + a + a = 9 + 7. Ensuite en enlevant 4 de chaque côté, l’égalité est maintenue, et l’on analyse alors l’équation a + a = 9 + 3.
- Faire des essais systématiques.
Proposer d’autres situations d’égalité similaires.
Ensuite, inviter les élèves à explorer des situations d’égalité contenant des variables.
Exemple

Demander aux élèves d’écrire une équation qui représente la situation d’égalité, puis de remplacer une variable par une valeur et de déterminer la valeur de l’autre.
Exemple
6 + c = 5 + s + 4
Si c = 3, alors s = 0
Si c = 10, alors s = 7
Note : Les différentes valeurs peuvent être écrites dans une table de valeurs.
| c | 3 | 10 | |||
|---|---|---|---|---|---|
| s | 0 | 7 |
Source : Guide d’enseignement efficace des mathématiques de la 4e à la 6e année, p. 186-187.
Activité 2 : le champ de fraises
Un producteur de fraises a 768 plants à mettre en terre cette année. Il a, en tout, 24 rangées dans son jardin qui sont prêtes à accueillir de 30 à 35 plants chacune. À l’aide d’une disposition rectangulaire, détermine le nombre de plants par rangée que le producteur devra mettre en terre pour que toutes les rangées de fraisiers soient de la même longueur.

Le champ de fraises (feuille de réponses)
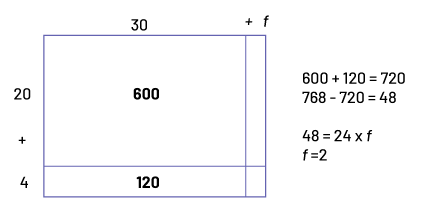 Image Sur un
rectangle, deux lignes sont perpendiculaires, au coin droit, en bas du rectangle.
Image Sur un
rectangle, deux lignes sont perpendiculaires, au coin droit, en bas du rectangle.
Le rectangle mesure 30 plus « f » de longueur.
Le rectangle mesure 20 plus 4 de largeur.
Dans le plus grand espace du rectangle, on peut lire : 600.
Dans un autre espace plus petit : 120.
Donc, il a besoin de mettre en terre 32 plants par rangée.
Source : L’@telier - Ressources pédagogiques en ligne (atelier.on.ca).
Activité 3 : Roule des égalités!
Tracer, en gros, au tableau, le signe = et expliquer l’activité :
Nous allons créer des équations à l’aide de dés et de mosaïques géométriques. À tour de rôle, deux élèves lancent deux dés et choisissent au hasard une mosaïque géométrique. Les nombres sur les dés de l’élève A et sa mosaïque géométrique seront utilisés pour créer l’expression algébrique qui apparaîtra à la gauche du signe = dans l’équation et ceux de l’élève B constitueront l’expression algébrique à la droite du signe.
Par exemple, si l’élève A obtient 3 et 4 sur les dés et tire un triangle vert, elle ou il écrira 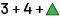 à la gauche du signe =.
à la gauche du signe =.

Si l’élève B obtient 4 et 6 sur les dés et tire un losange beige, elle ou il écrira 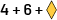 à la droite du signe =.
à la droite du signe =.

On crée ainsi l'équation 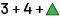 =
= 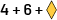 .
.
Il faut ensuite assigner des valeurs aux mosaïques géométriques tout en s’assurant de maintenir la relation d’égalité; par exemple, si l’élève A donne la valeur 4 au triangle vert, l’élève B doit donner la valeur 1 au losange beige.
Rappeler aux élèves que, dans une équation, deux symboles différents, comme un triangle vert et un losange beige, peuvent avoir la même valeur, mais que deux symboles identiques, comme deux losanges beiges, ont toujours la même valeur.
Il est possible que, dans certaines situations, l’égalité ne puisse être établie; par exemple, dans l’équation  , l’égalité ne
peut être établie. Donc, cette équation est rejetée.
, l’égalité ne
peut être établie. Donc, cette équation est rejetée.
Source : Guide d’enseignement efficace des mathématiques de la 4e à la 6e année, p. 132.
