C2.3 Solve equations that involve multiple terms, whole numbers, and decimal numbers in various contexts, and verify solutions.
Skill: Solving Equations that Include Multiple Terms, Whole Numbers and Decimal Numbers, in a Variety of Contexts
In Focusing on K-12 Algebraic Reasoning (Ontario Ministry of Education, 2013), it is explained that "[…] many students do not recognize that the equal sign indicates equality" (p. 6), or even equivalence between two numerical expressions. "[…] most students interpreted the equal symbol as synonymous with performing a calculation and [writing] the answer after the equal symbol" (p. 6).
This idea comes from an association made with arithmetic where the learner is often asked to evaluate equations with the form: a [operation sign] b = ? Furthermore, the use of the calculator reinforces this idea, as the answer is displayed when the student presses the "=" key. Therefore, it is necessary to present students with arithmetic situations that require them to check whether equalities are true or false (for example, 14 + 3 = 16 + 1), as well as equalities with unusual forms (17 = 3 + 14). To facilitate the transition from arithmetic to algebraic reasoning, students need to develop some skills related to relationships between quantities.
Source: translated from Guide d’enseignement efficace des mathématiques de la 7e à la 10e année, Fascicule 2, Algèbre, p. 26.
Skill: Recognizing a Situation of Equivalence
"To recognize an equality situation is to identify that two quantities have the same value" (Ontario Ministry of Education, 2008 a, p. 75). Using concrete and pictorial representations to represent an equality facilitates transfer to equalities represented with symbols. If students are adept at using the array model, then recognizing an equality situation and demonstrating it using algebraic expressions becomes more concrete for them.
Source: translated from Guide d’enseignement efficace des mathématiques de la 7e à la 10e année, Fascicule 2, Algèbre, p. 27.
Skill: Maintaining a Situation of Equivalence
Maintaining a situation of equivalence means operating on quantities to ensure that equality is maintained. By exploring various situations, students see that when a quantity is added to or removed from one member of an equality, the same action must be performed on the other member of the equality. These actions can be visualized with the pan balance.
Example
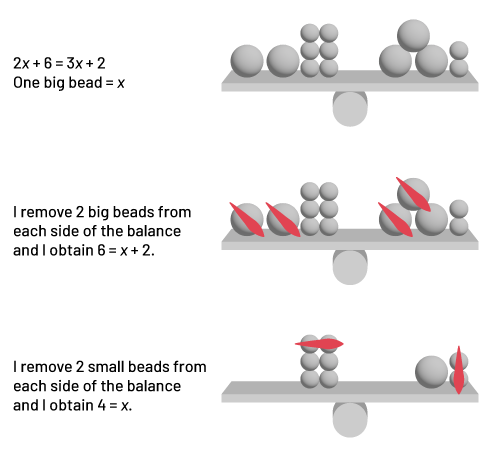
Without the representation of the pan balance, it is possible to solve the equation algebraically:
| \(2x + 6 = 3x + 2\) | |
|---|---|
| \(2x + 6 - 2x = 3x + 2 - 2x\) | I remove 2x from each side of the equal sign. |
| \(6 - 2 = x + 2 - 2\) | I remove 2 on each side of the equal sign. |
| \(4 = x\) | I determine the value of x. |
Understanding the process of maintaining equality is a very important skill that enables students to solve equations in all grades. Solving an equation involves grouping variables on one side and numbers on the other, while maintaining balance between the left side and right side.
Example
| \(4(x - 5) + 2x = 3x + 7\) | |
|---|---|
| \(4x - 20 + 2x = 3x + 7\) | I use the distributivity property. |
| \(\begin{align}4x + 2x - 20 + 20 &= 3x + 7 + 20 \\ 6x &= 3x + 27 \\ 6x - 3x &= 3x - 3x + 27 \\ 3x &= 27 \end{align} \) | I group the variables on one side and the numbers on the other, while maintaining the balance between the left and right members. |
| \(\frac{3x}{3} = \frac{27}{3}\) | I divide each side by 3. |
| \(x = 9 \) | I determine the value of x. |
Source: translated from Guide d’enseignement efficace des mathématiques de la 7e à la 10e année, Fascicule 2, Algèbre, p. 30-31.
Skill: Verifying Solutions after Solving Equations
Once the student has solved an equation, getting into the habit of checking its solution by inserting that value into the original equation is an excellent practice to adopt. The student should simply substitute the variable with that value in both the left side (to the left of the equal sign) and the right side (to the right of the equal sign), and then determine if the same answer is obtained on each side of the equal sign.
Knowledge: Equation
A mathematical statement that has equivalent expressions on both sides of an equal sign.

Source: Ontario Curriculum, Mathematics Curriculum, Grades 1-8, 2020, Ontario Ministry of Education.
