C1.3 Determine pattern rules and use them to extend patterns, make and justify predictions, and identify missing elements in repeating, growing, and shrinking patterns involving whole numbers and decimal numbers, and use algebraic representations of the pattern rules to solve for unknown values in linear growing patterns.
Activity 1: Determining Rules and Extending Patterns
Divide the class into teams. Create stations in the classroom and present different cards to the teams. (Allow about 10 minutes per station, then rotate.) Each card contains a table of values or a graph that is defined by a situation. Team members must answer a series of questions at each station during the allotted time. Circulate among the students and record their strategies. Involve the teams by debriefing as a class.
Examples of Problems
Station 1
The table of values below shows the number of pages Romi reads when she sits comfortably to read her favourite novel without interruption.
| Number of Hours of Reading (h) | 2 | 4 | 6 | 8 |
|---|---|---|---|---|
| Pages Read (p) | 50 | 100 | 150 | 200 |
- What is the constant rate?
- Which pattern rule defines this situation?
- How many pages did Romi read after 5 hours? after 11 hours? Explain your answer.
- How far will this pattern continue? Justify your answer.
Station 2
Using a dropper, drop 10 drops of oil into a beaker filled with water. The drops fall in approximately the same place so as to form a single circle. Then measure the diameter of the circle obtained after dropping 10, 20, 30, 40 and 50 drops of oil.
Here is the graphical representation of the relationship between the number of oil drops and the diameter of the circle obtained:
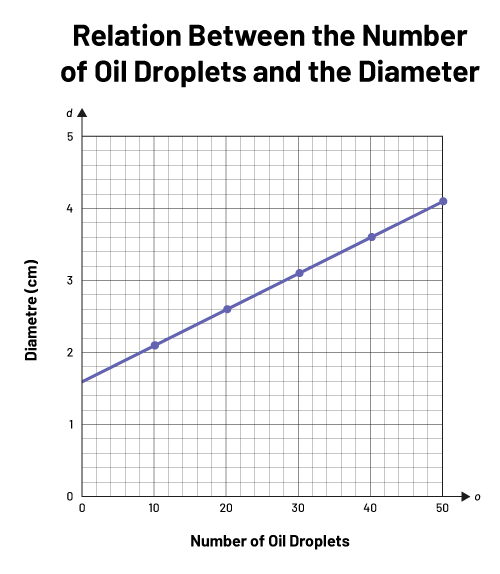
a) What is the diameter of the circle if 15 drops of oil are dropped into a beaker filled with water?
b) What will be the diameter of the circle if 60 drops of oil are dropped into a beaker filled with water? Determine your answer using an equation and another strategy of your choice.
Source: translated from En avant, les maths!, 7e année, CM, Algèbre, p. 3.
Station 3
A bakery has $15 in its cash drawer. If the average sales are $50.75 each hour,
- at this rate, determine how much money will be available in the cash drawer in 4 hours.
- at this rate, determine how much money will be available in the cash drawer in 12 hours.
Station 4
Extend this growing pattern. Predict the 10th term and the 50th term.
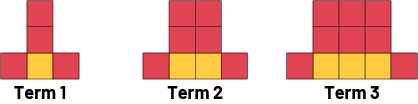
Source: translated from En avant, les maths!, 7e année, CM, Algèbre, p. 6.
Station 5
A teacher with an orchard at home put 80 apples that she picked in a large basket at the front of the classroom for her students. The number of apples steadily decreased each hour. She counted the number of apples in the container from time to time. The results are shown in the following table of values.
| Number of Hours Elapsed | Apples in the Basket |
|---|---|
| 0 | 80 |
| 1 | 72 |
| 2 | 64 |
| 3 | 56 |
| 4 | |
| 5 | 40 |
| 6 | 32 |
| 7 | |
| ... | ... |
- How many apples were left in the basket after four hours? Justify your answer.
- How many apples were left in the basket after seven hours? Justify your answer.
- After how many hours will there be no apples left in the basket?
Activity 2: Predictions Based on Recursive Relationships
Divide the class into teams. Give them a situation. From this, students individually create a numeric pattern representing the situation (encourage them to use a table of values to organize their data). Afterwards, students describe their pattern. Each situation should lead students to predict an outcome.
Examples of Scenarios
A) Arturo opens a savings account and puts in an initial amount of $75. Then, at the end of each month, he will deposit $40.
- If the conditions remain the same, how much money will Arturo have after the first 5 months?
- How much money will he have after 1 year?
- What do you notice about the numbers in this pattern?
Note: Students should be able to point out the constant rate and the initial value, and explain what this means in this context.
To take this further, ask students to find/create situations where they can create repeating, growing and shrinking patterns.
B) Carla complies with the speed limit for bike lanes in her area by riding at a speed of 20 kilometres per hour. Determine the number of kilometres she travels in four hours using a table of values, a graph and an equation.
C) Use your knowledge of linear growing patterns, constant rates and initial values to represent the growing pattern below by its equation, table of values and graph.
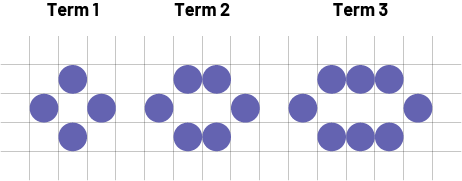
Source: translated from En avant, les maths!, 7e année, CM, Algèbre, p. 7.
