C1.3 Déterminer et utiliser les règles pour prolonger des suites, faire et justifier des prédictions, et trouver les termes manquants dans des suites à motif répété, des suites croissantes et des suites décroissantes comprenant des nombres naturels et des nombres décimaux, et utiliser les représentations symboliques des règles pour trouver des valeurs inconnues dans des suites croissantes linéaires.
Activité 1 : des prédictions calculées (déterminer des règles et prolonger des suites)
Diviser le groupe-classe en équipes. Créer des stations dans la salle de classe et y présenter des fiches différentes aux équipes. (Allouer environ 10 minutes par station, puis faire une rotation.) Chaque fiche contient une table de valeurs ou une représentation graphique qui est définie par une mise en situation. Les membres de l’équipe doivent répondre à une série de questions à chaque station pendant le temps alloué. Circuler parmi les élèves et noter leurs stratégies. Faire participer les équipes en faisant un retour en groupe-classe.
Exemples de problèmes par station
Station 1
Le tableau ci-dessous présente le nombre de pages que lit Romi lorsqu’elle s’assoit confortablement pour lire son roman préféré sans interruption.
| Nombre d’heures de lecture (h) | 2 | 4 | 6 | 8 |
|---|---|---|---|---|
| Pages lues (p) | 50 | 100 | 150 | 200 |
- Quel est le taux de variation constant?
- Quelle règle de correspondance définit cette situation?
- Combien de pages Romi a-t-elle lues après 5 heures? après 11 heures? Expliquez votre réponse.
- Jusqu’où cette suite va-t-elle se poursuivre? Justifiez votre réponse.
Station 2
À l’aide d’un compte-gouttes, on laisse tomber 10 gouttes d’huile dans un bécher rempli d’eau. Les gouttes tombent à peu près au même endroit de manière à former un seul cercle. Ensuite, on mesure le diamètre du cercle obtenu après avoir laissé tomber 10, 20, 30, 40 et 50 gouttes d’huile.
Voici la représentation graphique de la relation entre le nombre de gouttes d’huile et le diamètre du cercle obtenu :
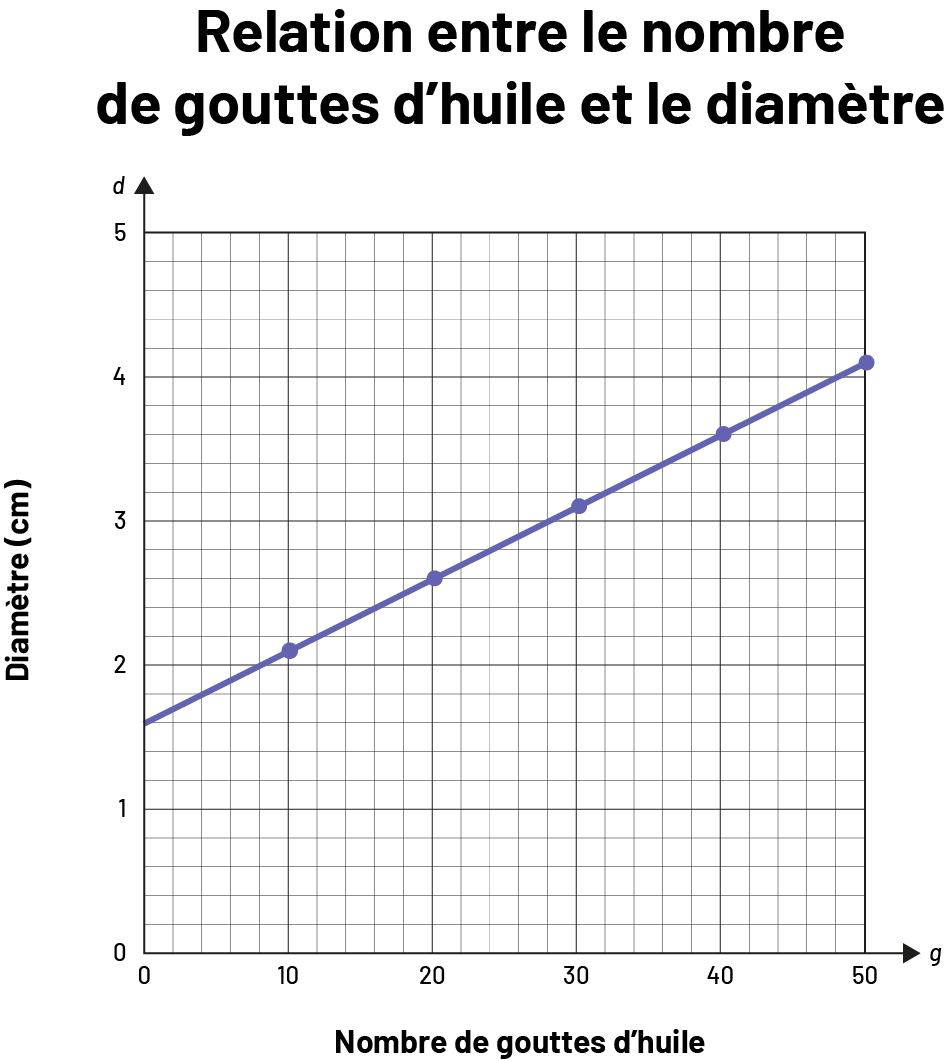
a) Quel sera le diamètre du cercle si on laisse tomber 15 gouttes d’huile dans un bécher rempli d’eau?
b) Quel sera le diamètre du cercle si on laisse tomber 60 gouttes d’huile dans un bécher rempli d’eau? Déterminez votre réponse à l’aide d’une équation et d’une autre stratégie de votre choix.
Source : En avant, les maths!, 7e année, CM, Algèbre, p. 3.
Station 3
Une boulangerie compte 15 dollars dans son tiroir-caisse. Si en moyenne les ventes sont de 50,75 $ chaque heure,
- à ce rythme, déterminez combien d’argent sera disponible dans le tiroir-caisse dans quatre heures.
- à ce rythme, déterminez combien d’argent sera disponible dans le tiroir-caisse dans 12 heures.
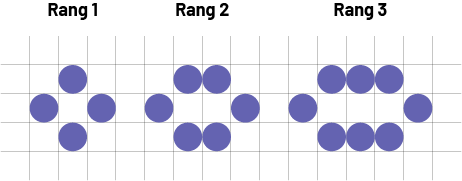
Station 4
Prolonger cette suite croissante. Prédire la figure au 10e rang et celle au 50e rang.
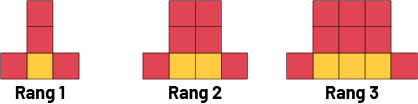
Source : En avant, les maths!, 7e année, CM, Algèbre, p. 6.
Station 5
Une enseignante ayant un verger chez elle a mis 80 pommes qu’elle a cueillies dans un gros panier à l’entrée de la classe pour ses élèves. Le nombre de pommes diminue de façon constante chaque heure. Elle a compté le nombre de pommes dans le contenant de temps en temps. Les résultats sont présentés dans la table de valeurs suivante.
| Nombre d'heures écoulées | Pommes dans le panier |
|---|---|
| 0 | 80 |
| 1 | 72 |
| 2 | 64 |
| 3 | 56 |
| 4 | |
| 5 | 40 |
| 6 | 32 |
| 7 | |
| ... | ... |
- Combien de pommes restait-il dans le panier après quatre heures? Justifiez votre réponse.
- Combien de pommes restait-il dans le panier après sept heures? Justifiez votre réponse.
- Après combien d’heures ne restera-t-il plus de pommes dans le panier?
Activité 2 : des prédictions basées sur les règles de régularité
Diviser le groupe-classe en équipes. Leur donner une mise en situation. À partir de celle-ci, les élèves créent individuellement une suite de nombres représentant la situation (les encourager à utiliser une table de valeurs afin d’organiser leurs données). Par la suite, les élèves décrivent leur régularité. Chaque mise en situation devrait amener les élèves à prédire un résultat.
Exemples de mises en situation
- Arturo ouvre un compte d’épargne et y place un montant initial de 75 $. Par la suite, à la fin de chaque mois, il y déposera un montant de 40 $.
- Si les conditions restent les mêmes, combien d’argent Arturo aura-t-il après les 5 premiers mois?
- Combien d’argent aura-t-il après 1 an?
- Que remarques-tu à propos des nombres que forme cette suite?
Note : Les élèves devraient être en mesure de faire ressortir le taux de variation constant et la valeur initiale, et d’expliquer ce que cela signifie dans ce contexte.
Pour aller plus loin, demander aux élèves de trouver/d’inventer des situations afin qu’elles et ils puissent créer des suites à motif répété, des suites croissantes et des suites décroissantes. Voici quelques exemples :
- Carla respecte la limite de vitesse des pistes cyclables de sa région en roulant à une vitesse de 20 kilomètres par heure. Détermine le nombre de kilomètres qu’elle parcourt en quatre heures à l’aide d’une table de valeurs, d’une représentation graphique et d’une équation.
- Utilise tes connaissances des suites croissantes linéaires, des taux constants et des valeurs initiales afin de représenter la suite croissante ci-dessous par son équation, sa table de valeurs et sa représentation graphique.