GEEM - Skills and Knowledge

C2.2 Evaluate algebraic expressions that involve rational numbers.

Skill: Evaluating Algebraic Expressions Involving Rational Numbers

To evaluate an algebraic expression, the variables are replaced with numerical values and calculations are performed based on the order of operations.

When students are working with formulas, they are evaluating expressions.

Replacing the variables with numerical values often requires the use of brackets. For example, the expression $\frac{3}{4}$ m becomes $\frac{3}{4}$ (m) and then $\frac{3}{4}$ ( $\frac{2}{5}$ ) when m = $\frac{2}{5}$ The operation between $\frac{3}{4}$ and $\frac{2}{5}$ is understood to be multiplication.

Source: Ontario Curriculum, Mathematics Curriculum, Grades 1-8, 2020, Ontario Ministry of Education.

Example

Evaluate the algebraic expression $2 a + b - 1$ , if $a = \frac{1}{2}$ and $b = \frac{1}{4}$ .

STRATEGY 1
Visual Representation

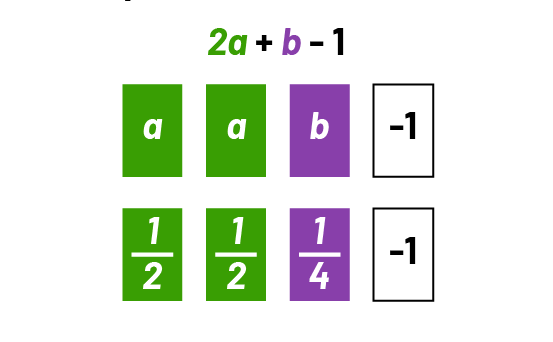
I know that $2 a + b - 1$ means 2 groups of a plus b minus 1. I replace the variable
a by $\frac{1}{2}$ and the variable b by $\frac{1}{4}$ . I calculate $(2 g r o u p s o f \frac{1}{2}) + \frac{1}{4} - 1$ .
This is 1 + 1 - 1. This makes 1 - 1 cancel out.

STRATEGY 2
Symbolic Representation

$\begin{aligned} 2 a + b - 1 & = 2 \times \frac{1}{2} + \frac{1}{4} - 1 \\ = 1 + \frac{1}{4} - 1 \\ = \frac{1}{4} \end{aligned}$

Source: translated from En avant, les maths!, 8^e année, CM, Algèbre, p. 3.