C2.2 Évaluer des expressions algébriques qui comprennent des nombres rationnels.
Habileté : évaluer des expressions algébriques comprenant des nombres rationnels
Pour évaluer une expression algébrique, il faut remplacer les variables par des valeurs numériques et faire les calculs selon la priorité des opérations.
Lorsque les élèves travaillent avec des formules, elles et ils évaluent des expressions.
Substituer des variables par des valeurs numériques nécessite souvent l’utilisation de parenthèses. Par exemple, l’expression \(\frac{3}{4}\)m devient \(\frac{3}{4}\) (m) puis \(\frac{3}{4}\) (\(\frac{2}{5}\)) lorsque m = \(\frac{2}{5}\). L’opération entre \(\frac{3}{4}\) et \(\frac{2}{5}\) est la multiplication.
Source : Curriculum de l’Ontario, Programme-cadre de mathématiques de la 1re à la 8e année, 2020, Ministère de l’Éducation de l’Ontario.
Exemple
Évalue l’expression algébrique \(\ 2a + b \ – \ 1\), si \(\ a = \frac{1}{2}\) et \(\ b = \frac{1}{4}\).
STRATÉGIE 1
Représentation visuelle
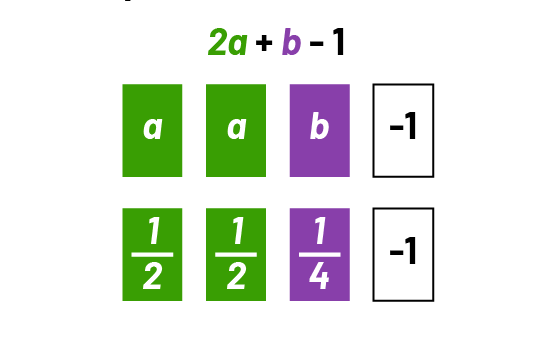
Je sais que \(\ 2a + b \ – 1\) signifie 2 groupes de a plus b moins 1. Je remplace la variable
a par \(\frac{1}{2}\) et la variable b par \(\frac{1}{4}\). Je calcule (\(\mathord{2 \ groupes \ de} \ \frac{1}{2}\ \)) + \(\ \frac{1}{4}\ - 1\). C’est \(\ 1 + \frac{1}{4} - 1 \).
Ce qui fait \(\frac{1}{4}\) puisque le \(\ 1 – 1\) s’annule.
STRATÉGIE 2
Représentation symbolique
\(\displaylines{\begin{align} 2a + b - 1 &= 2 \times \frac{1}{2}\ + \frac{1}{4}\ - 1 \\ &= 1 + \frac{1}{4} \ - 1 \\ &= \frac{1}{4} \end{align}}\)
Source : En avant, les maths!, 8e année, CM, Algèbre, p. 3.
