C1.1 Identify and compare a variety of repeating, growing, and shrinking patterns, including patterns found in real-life contexts, and compare linear growing and shrinking patterns on the basis of their constant rates and initial values.
Activity 1: Compare Equations of Growing and Shrinking Patterns
Divide students into teams. Prepare a series of equations in the form y = mx + b. Ask students to compare the equations, and use a graphical representation and a table of values to help determine their constant rates and the initial values. Have students sort the equations by the type of patterns they are representing growing or shrinking. Encourage discussion among team members.
Example
Identify and compare the constant rates and initial values of the following equations:
| \(C = 4x + 5\) | \(C = -2x + 5\) |
| \(C = 2x + 10\) | \(C = -4x + 10\) |
Which ones are growing? shrinking? How do you know?
Activity 2: A Shrinking Pattern
Divide the students into teams. Present the pattern to them and ask the teams to identify all the properties related to this pattern and to justify their statements.
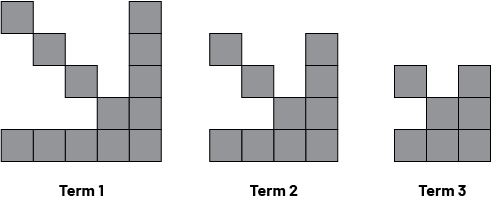
Ensure that they consider the term number, the initial value and the constant rate. In addition, they should be able to tell if it is growing or shrinking.
Ask the following question:
- Can this pattern continue to infinity? Explain.
Complete the analysis by asking them to graph the pattern.
Ask the question:
- Should the points be connected in the graph? Why do they have to be connected?
Activity 3: The Constant Rate and the Initial Value of a Linear Pattern
Project graphical representations of linear patterns on the board. See example. Label each of the lines. Students analyze and work individually. Discuss the students' solutions as a class.
Examples of lines and instructions
- Determine the constant rate for each of the lines, and order them in increasing order.
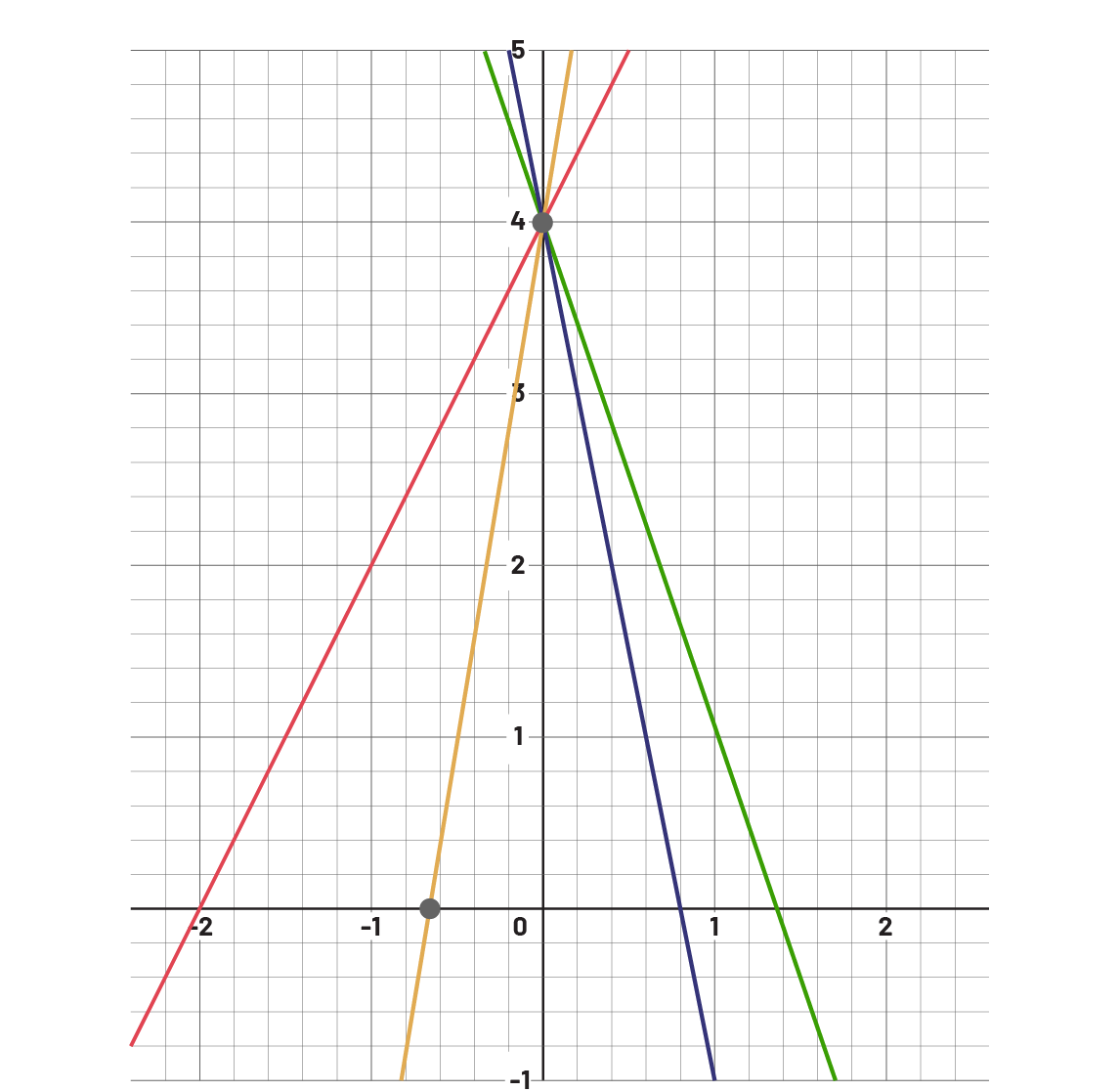
- Determine the initial value for each of the following lines and order them in increasing order.

