C1.1 Reconnaître et comparer une variété de suites à motif répété, de suites croissantes et de suites décroissantes, y compris des suites trouvées dans la vie quotidienne, et comparer des suites croissantes linéaires et des suites décroissantes selon leurs taux constants et leurs valeurs initiales.
Activité 1 : comparer des équations de suites croissantes et décroissantes
Diviser les élèves en équipes. Préparer une série d’énoncés sous la forme y = mx + b. Les élèves doivent comparer les équations, déterminer le taux de variation et la valeur initiale et dire lesquelles sont croissantes et lesquelles sont décroissantes. Encourager la discussion entre les membres des équipes.
Exemple
Identifiez et comparez les taux de variation constants et les valeurs initiales des droites suivantes :
| C = 4x + 5 | C = -2x + 5 |
| C = 2x + 10 | C = -4x + 10 |
Lesquelles sont croissantes? décroissantes? Comment le sais-tu?
Activité 2 : la suite cachée (suite décroissante)
Diviser les élèves en équipes. Leur présenter la suite et inviter les équipes à ressortir toutes les propriétés liées à cette suite de figures et à justifier leurs affirmations.
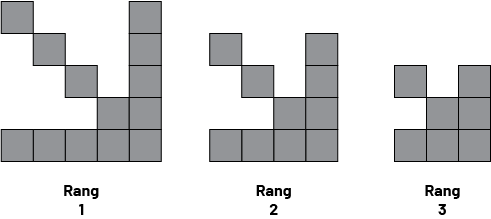
Premier rang : 5 carrés superposés horizontalement et 5 carrés superposés verticalement, et 4 carrés en diagonale à partir du centre. Rang 2 : 4 carrés superposés horizontalement et 4 carrés superposés verticalement, et 3 carrés en diagonale à partir du centre. Rang 3 : 3 carrés superposés horizontalement et 3 carrés superposés verticalement, et 2 carrés en diagonale par rapport au centre.
S’assurer qu’elles et ils considèrent le rang, la valeur initiale et le taux de variation constant. De plus, elles et ils devraient être capables de dire si celle-ci est croissante ou décroissante.
Poser ensuite la question suivante :
- Est-ce que cette suite peut continuer jusqu’à l’infini? Expliquez.
Terminer l’analyse en leur demandant de représenter la suite sous forme de représentation graphique.
Poser la question :
- Les points doivent-ils être reliés dans la représentation graphique? Pourquoi?
Activité 3 : taux de variation et valeur initiale d’une suite linéaire
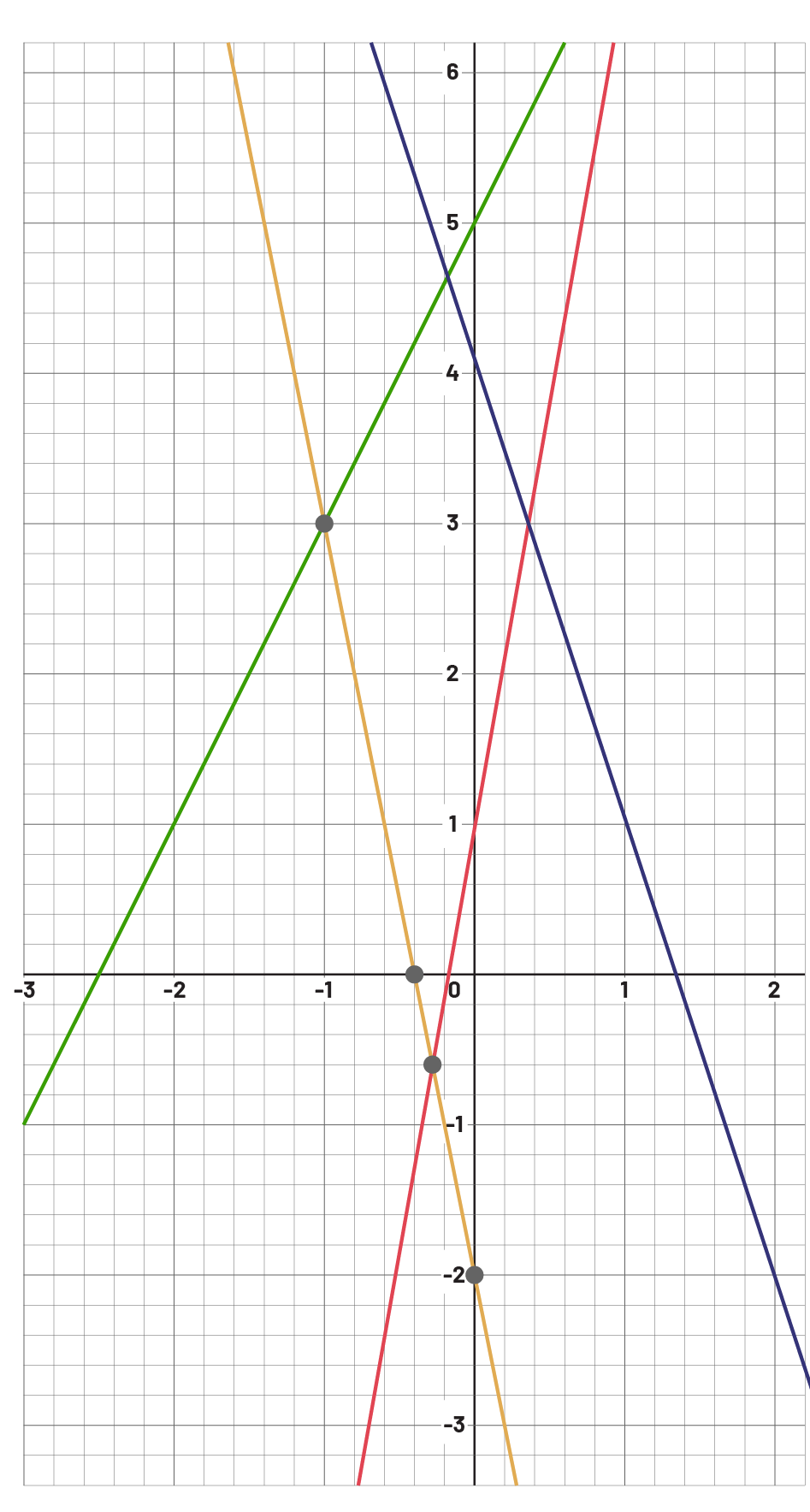
Projeter les représentations graphiques de suites linéaires au tableau interactif. À partir des couleurs des droites, l’élève doit répondre aux consignes demandées. L’élève analyse et travaille individuellement. Faire un retour en groupe-classe et discuter des solutions des élèves.
Exemples de droites et de consignes
- Classe les droites suivantes, représentant des suites linéaires, en ordre croissant de taux de variation.
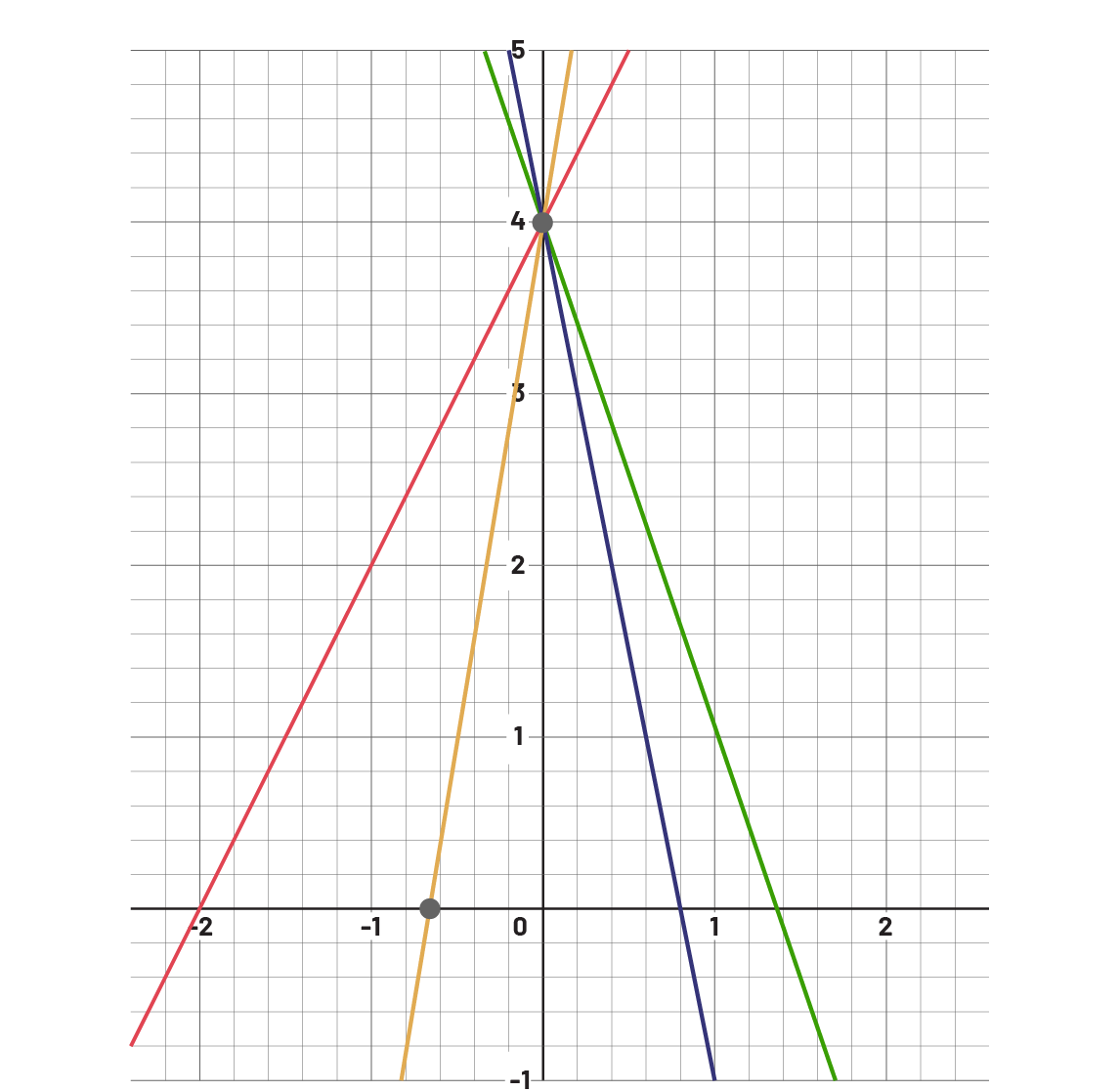
Représentation graphique de suite linéaire : L’axe à l’ordonnée est de moins un à 5. L’axe de l’abscisse est de moins 2 à 2. 4 droites, avec des taux de variations différents, sont représentées sur le graphique et se croissent aux coordonnées (parenthèse ouvrante) zéro, 4 (parenthèse fermante).
- Classe les droites suivantes, représentant des suites linéaires, en ordre croissant de valeur initiale.