C1.2 Create and translate repeating, growing, and shrinking patterns involving rational numbers using various representations, including algebraic expressions and equations for linear growing and shrinking patterns.
Activity 1: Different Representations
Materials
- Grid paper
- Coloured pencils
Given the equation s = 3n + 2, the student will be responsible for answering a series of instructions. It is important for the student to be able to represent the pattern in different ways.
- Create a semi-concrete pattern on your grid paper representing the starting equation. Clearly indicate the pattern core on your drawing. Make sure you have at least 4 terms in the pattern.
- Represent the pattern in a table of values. Clearly indicate the meaning of the variables used.
- Draw a graphical representation of it on grid paper. What do you notice?
* Repeat the activity for an equation that represents a shrinking pattern.
Invite students to form teams so that they can compare their strategies and answers, providing feedback to each other. Repeat the same thing as a class to conclude.
Examples of strategies
Example 1
Representation : s = 3n + 2; s : number of squares n : term number
Nonnumeric increasing sequence of squares on a grid table. Rank 1: 2 red squares overlaying vertically and 3 green squares. overlaying verticallyRank 2: 2 red squares overlaying vertically and 6 green squares. overlaying verticallyRank 3: 2 red squares overlaying vertically and 12 green squares overlaying vertically.
Example 2
Nonnumeric increasing sequence of squares on a grid table. Rank 1: 2 red squares and 2 green squares underlaying vertically. one green squares on the side.Rank 2: 2 red squares and 4 green squares underlaying vertically. 2 green squares on the side. Rank 3: 2 red squares and 6 green squares underlaying vertically. 3 green squares on the side.
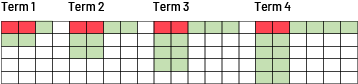
Possible questions
- Compare the patterns. What do you notice? Point out the similarities and differences.
- Are the resulting relationships and rules identical? Equivalent?
Note: When simplified, the rules should be equivalent to s = 3n + 2.
Activity 2: Let's Create Non-Linear Patterns
Materials: blocks, tiles, grid sheets, curve plotter software
Divide students into teams. Write the following instructions on the board:
- You must create a non-linear pattern using the material available.
- You need to represent your pattern with a table of values and a graphical representation.
- Finally, describe why this pattern is non-linear and describe its recursive relationship (from one term to the next).
Discuss as a class. Ask some teams to present their representations.
Activity 3: A Pattern of Hexagons
Project this picture on the board. Students must find a way to determine an equation to calculate the perimeter, p, of a chain of n hexagons.
Each team should have a table of values showing the perimeter as a function of the number of hexagons, and end with an equation that finds the perimeter. You can also have them graph the relationship.
Note: For students having difficulty, give clues as to which variables to use to find the equation.
Consolidate and compare students' strategies and answers. All equations that work should simplify to the same equation and graph.